Graphs

YOU ARE LEARNING:

Estimating the Area Under a Curve

Estimating the Area Under a Curve

In many situations, the area under a curve can tell us important information. We can estimate it by finding the areas of shapes which fit under the curve.

The area under a curve can be an important quantity to calculate. For example, in a speed-time graph, it represents the distance travelled.

Sometimes the area under a graph will be able to be calculated exactly because it is some kind of polygon such as a triangle, rectangle or trapezium.

Remember the formula for the area of a triangle

We will use triangles as a shape to estimate the area under a curve.

What is the area of a triangle with base $10$ and height $5$ ?

This is the formula for the area of a rectangle

We can also use rectangles as shapes to find the area under a curve.

What is the area of a rectangle with base $6$ and height $8$ ?

Trapeziums are also useful for finding the area under a curve

This is the formula for finding the area of a trapezium, where $a$ and $b$ are the lengths of the parallel sides.

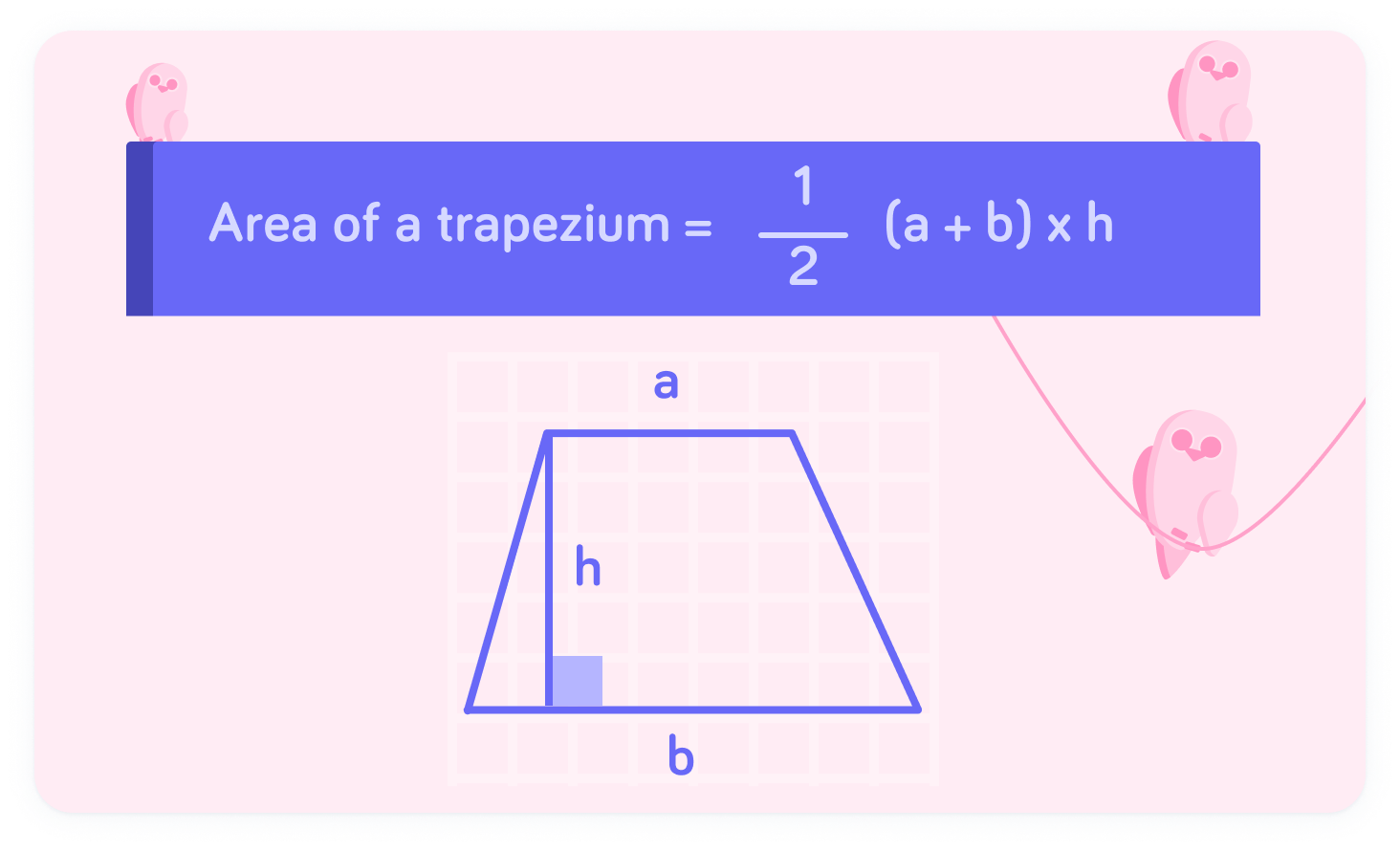
What is the area of a trapezium where $a=3$ , $b=5$ and $h=6$ ?

However, if the graph is curved we will have to estimate the area using either a triangle, rectangle or trapezium or a combination of them.