YOU ARE LEARNING:
Changing Fractions into Percentages and Decimals
Changing Fractions into Percentages and Decimals
This lesson helps you work out for example 7 twenty-fifths in percent.
100% is the same as 1
How do you find out what for example 52 is in %?

How would you find out how much 51 is out of 100%?
A) Divide 100% by 5 B) Divide 5 by 100%


What is 5100%?


So 51=20%. How much is 52 in % then?

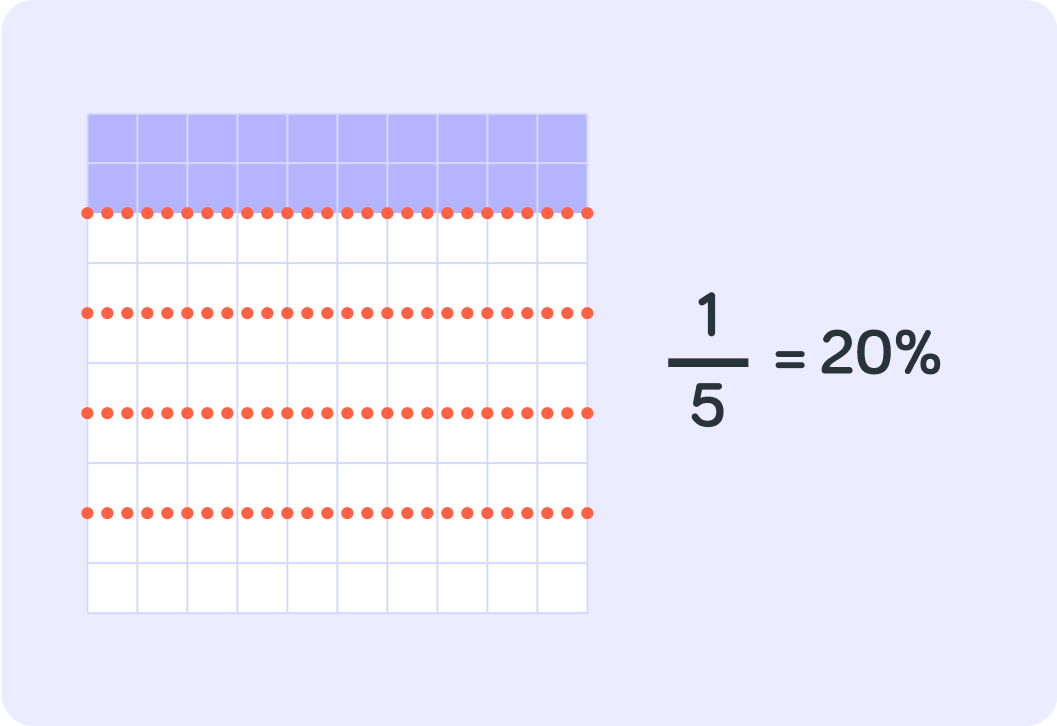
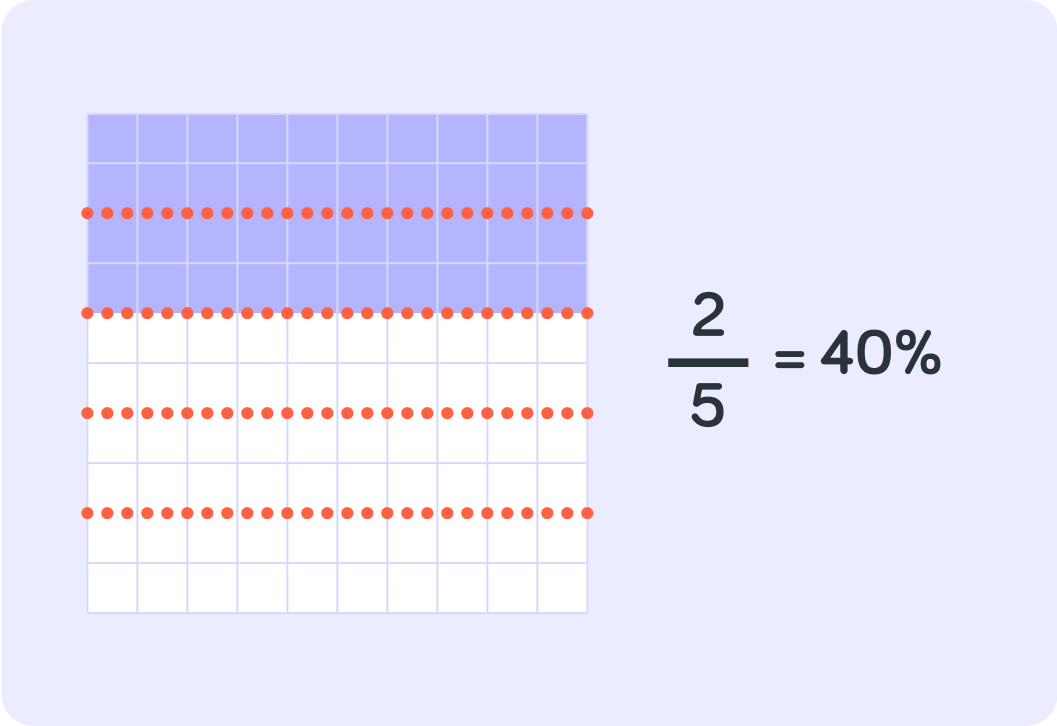
You found 52 in % like this
First you found 51 of 100% by saying 5100%=20% Then you found 52 of 100% by saying 20%×2=40%
How much is 257 in %?
First you need to find 251 of 100%
Then you find 257 of 100%
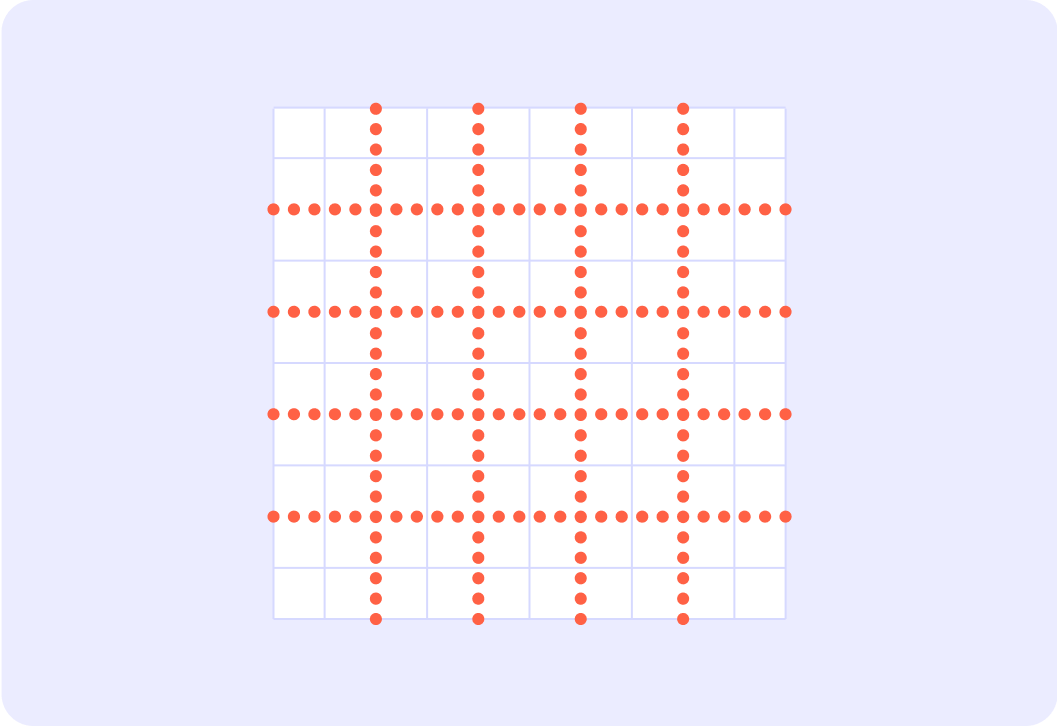
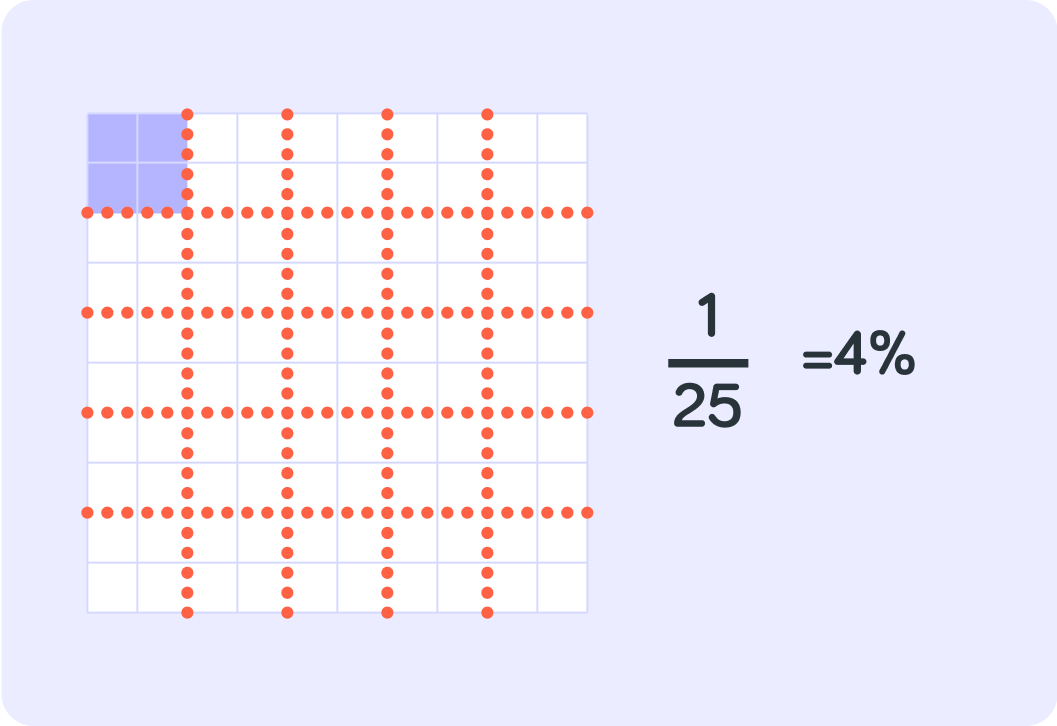
What is 251 of 100%?


So 251 or 25100% is 4%. How much is 257 in % then?

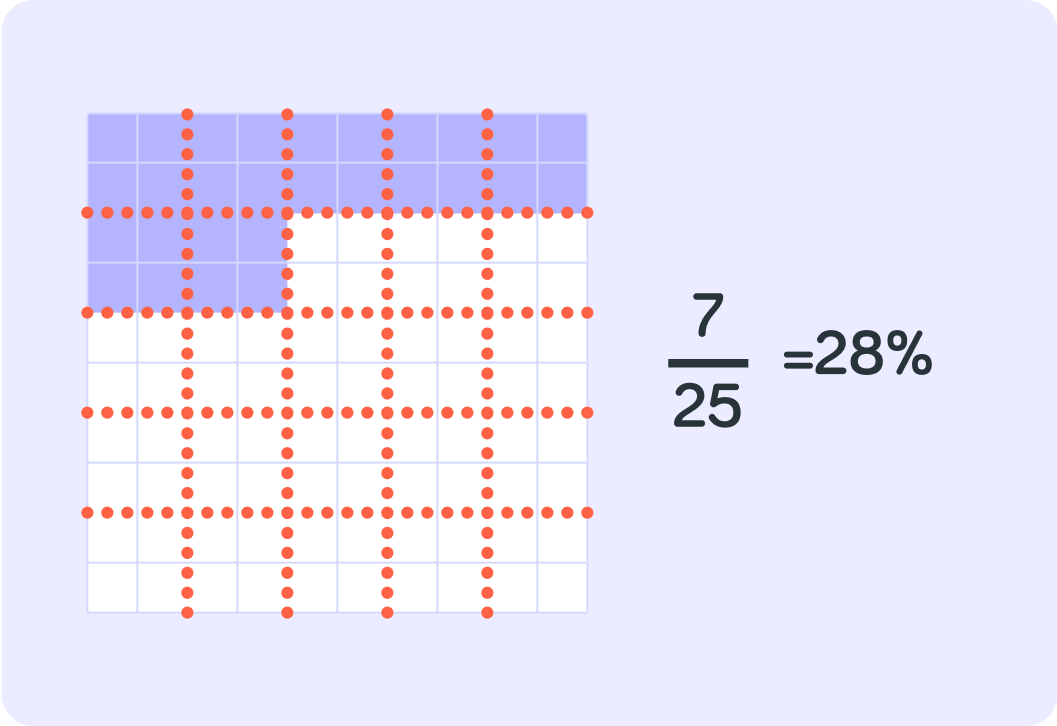
So 257 is the same as 28%
251 is 4%, so 257 is 4%×7=28%
How much is 83 in %?

How much is 209 in %?

Summary!
You can change fractions into percentages.

For example, find 257 in %
First you find 251 of 100% Then you find 257 of 100%
So 257 is the same as 28%

