Number

YOU ARE LEARNING:

Significant Figures

Significant Figures

Significant figures give us a general way to round numbers of any size to make them more readable.

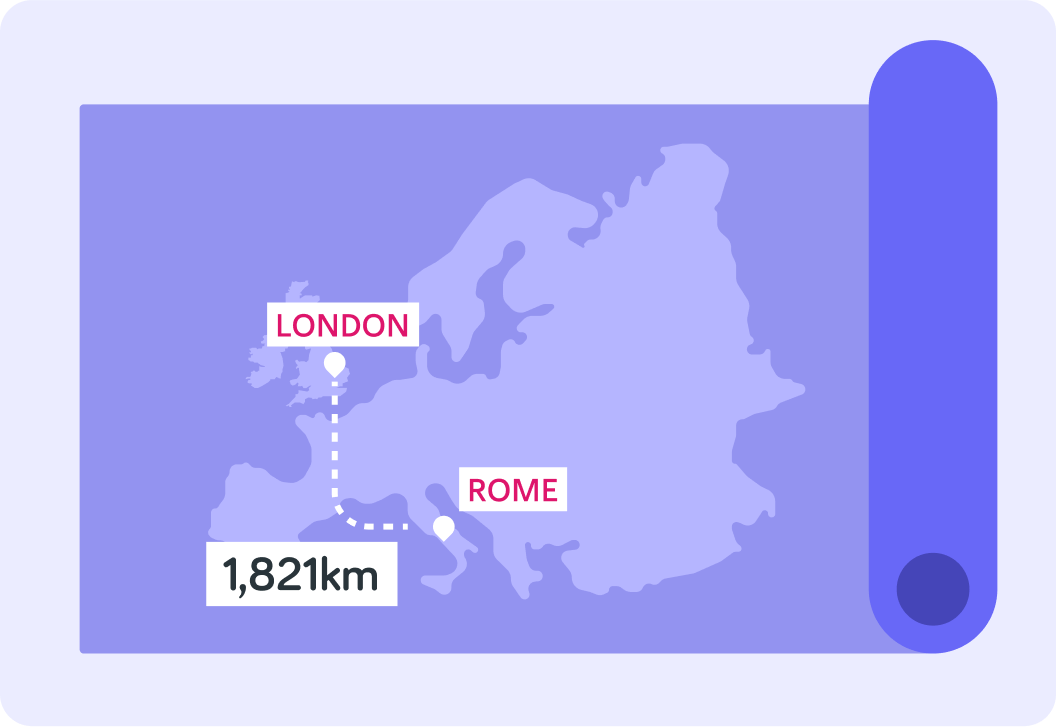
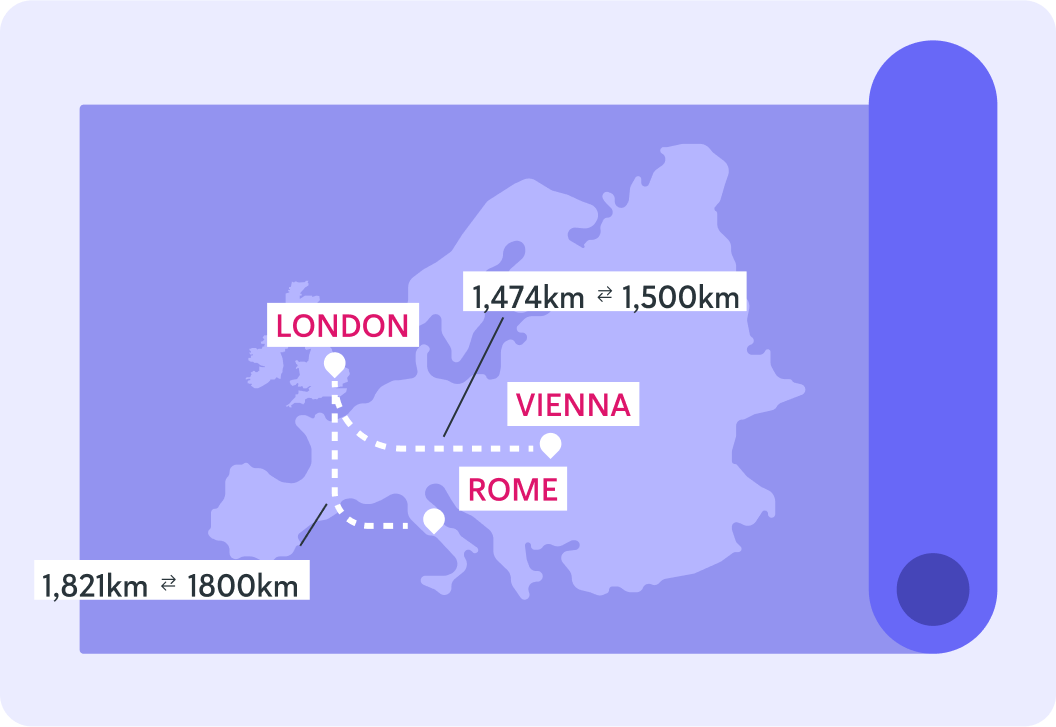
How far is the drive from London to Rome?

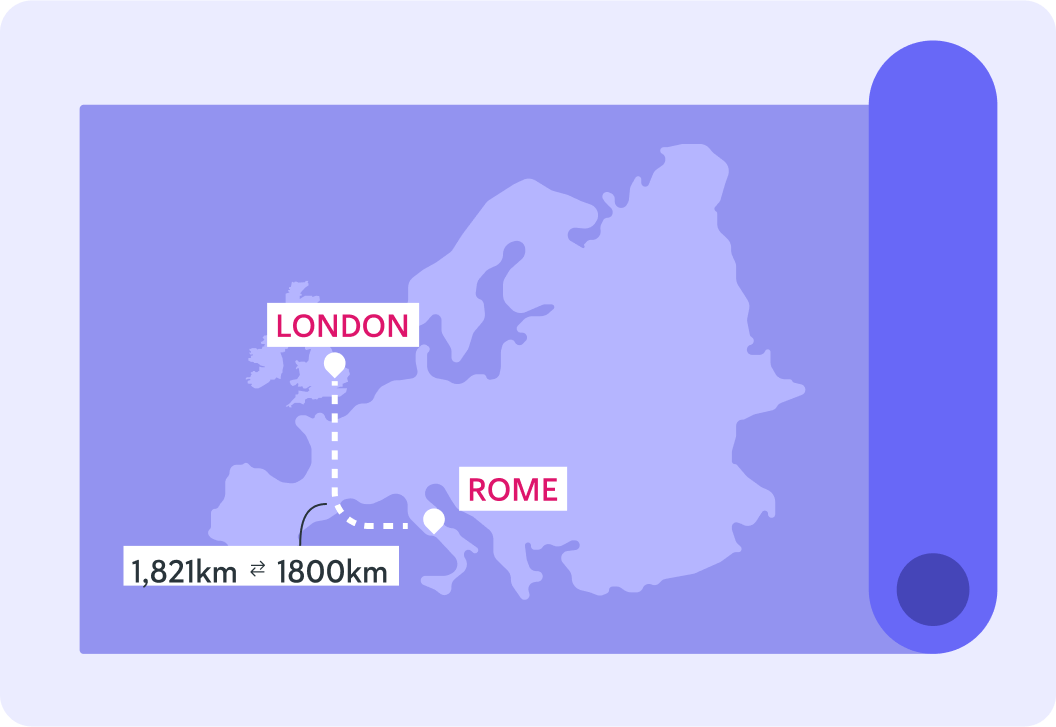
Now, to the nearest 100 kilometres, there are ______________ between London and Rome.

A) $2,000 \space km$ B) $1,900 \space km$ C) $1,800 \space km$

So you can give the distance from London to Rome as $1,821 \space km$ or slightly less precisely as $1,800 \space km$

$1,800 \space km$ might just be a little easier to remember, and $21 \space km$ more or less is just not that significant at these distances.

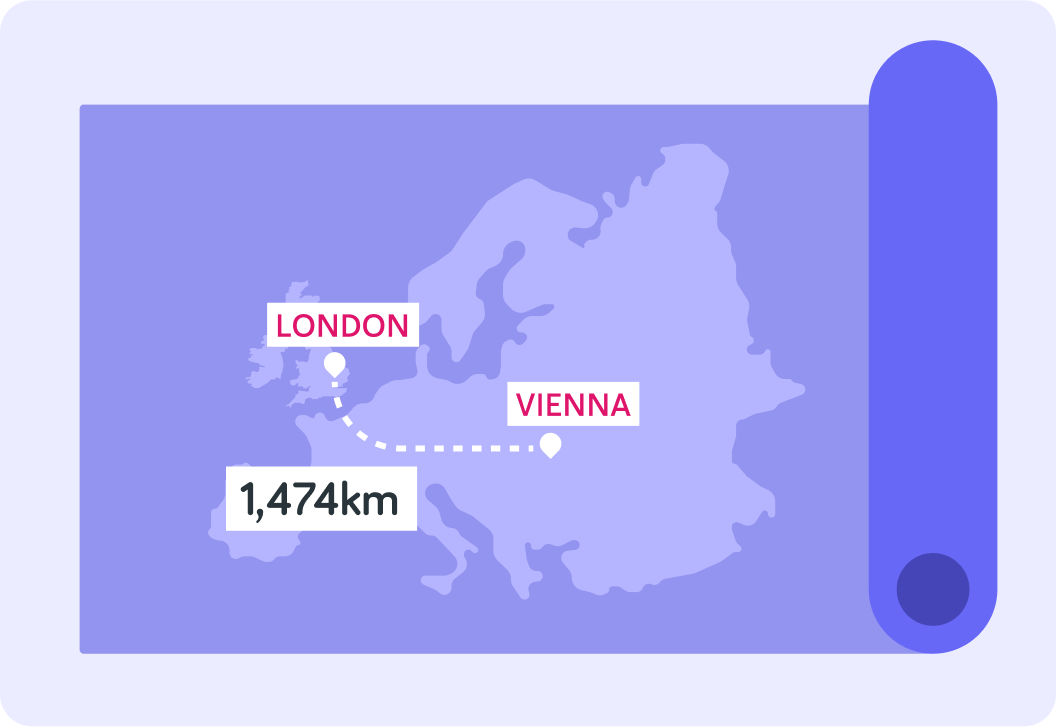
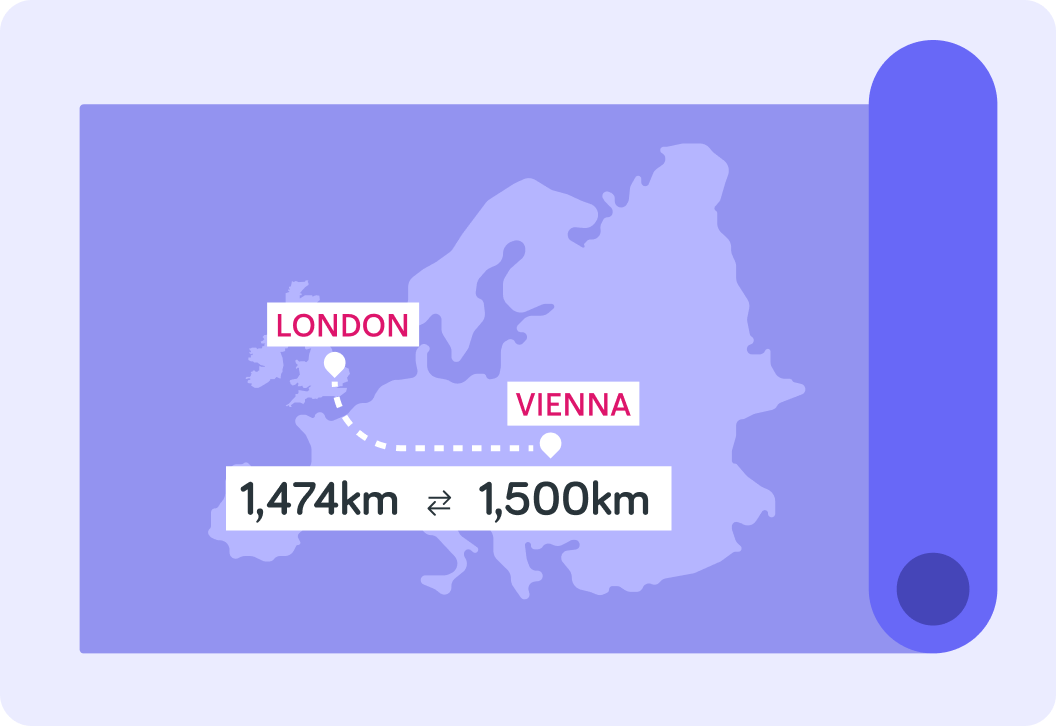
How far is the drive from London to Vienna?

Now, 100 kilometres more or less is not really that significant, so what is the distance between London and Vienna to the nearest 100 kilometres?

A) $1,500 \space km$ B) $1,470 \space km$ C) $1,400 \space km$

So you can give the distance from London to Vienna as $1,474 \space km$ or slightly less precisely as $1,500 \space km$

$1,500 \space km$ might just be a little easier to remember, and $26 \space km$ more or less is just not that significant at these distances.

For both trips, you rounded off the distance from 4 significant figures (SF) to just 2 significant figures

London - Rome to 4 SF: $1,821 \space km$ London - Rome to 2 SF: $1,800 \space km$

London - Vienna to 4 SF: $1,474 \space km$

London - Vienna to 2 SF: $1,500 \space km$

$1,821 \space km$ has 4 SF, but $1,800 \space km$ has only 2 SF. That means that zeros at the end of whole numbers ______ count as significant figures.

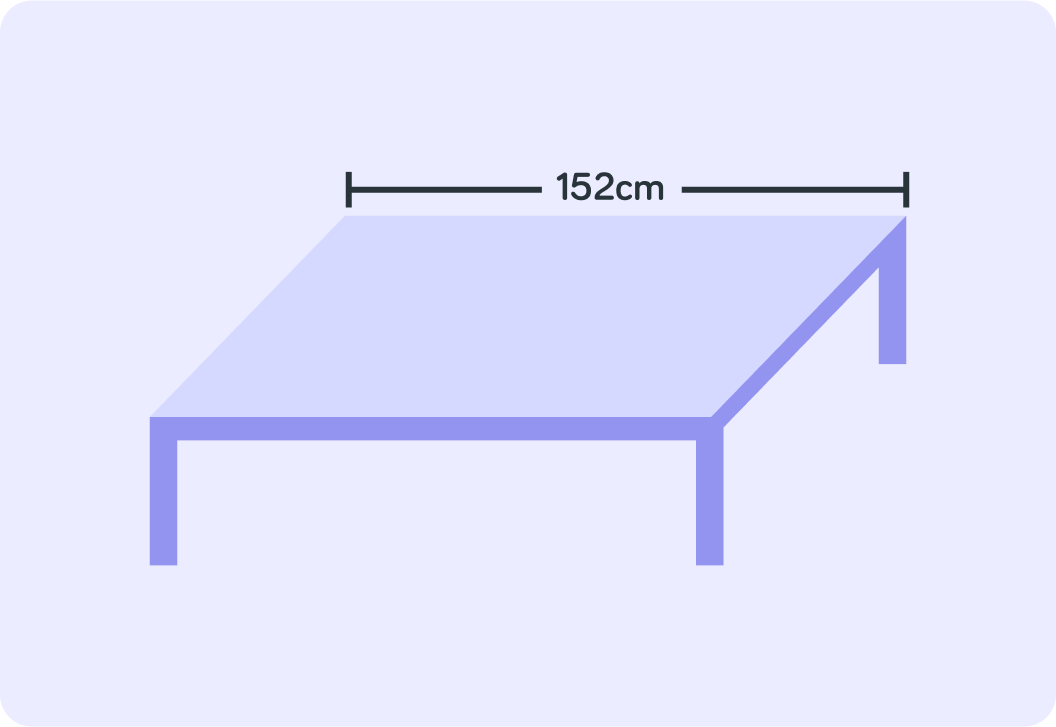
Imagine you have measured this table to $152 \space cm$ . How many significant figures does that contain?

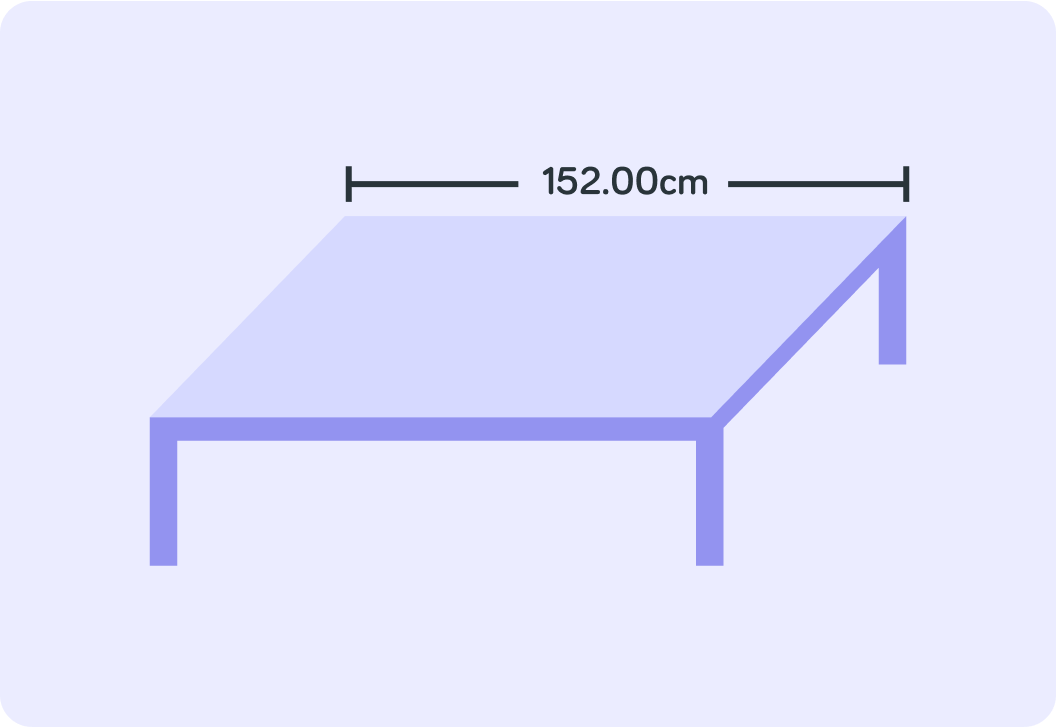
What if you had given your measurement as $152.00 \space cm$ instead of just $152 \space cm$ ?

The $.00$ makes it clear that the table is measured to precisely $152 \space cm$ - not $152.1 \space cm$ for example.

So the $.00$ in $152.00 \space cm$ says something about how precise this measurement is. Should they be considered as significant figures? Answer yes or no.

Zeros after the decimal point count as significant figures

They say something about how precise a number really is.

How many significant figures does $152.00 \space cm$ contain, then?

What if you didn't have to be that precise and you were told to round off $152.00 \space cm$ to just 3 SF. What would it be?

What if you could be even less precise and were asked to round off $152.00 \space cm$ to just 2 SF. What would that be?

So you can give your measurement of the table more precisely or less precisely depending on the number of significant figures

The more significant figures you give, the more important it is that the table is exactly $152.00 \space cm$

Why would you not always just give the most precise measure you have?

Why would you ever decide that some figures are not really that significant?

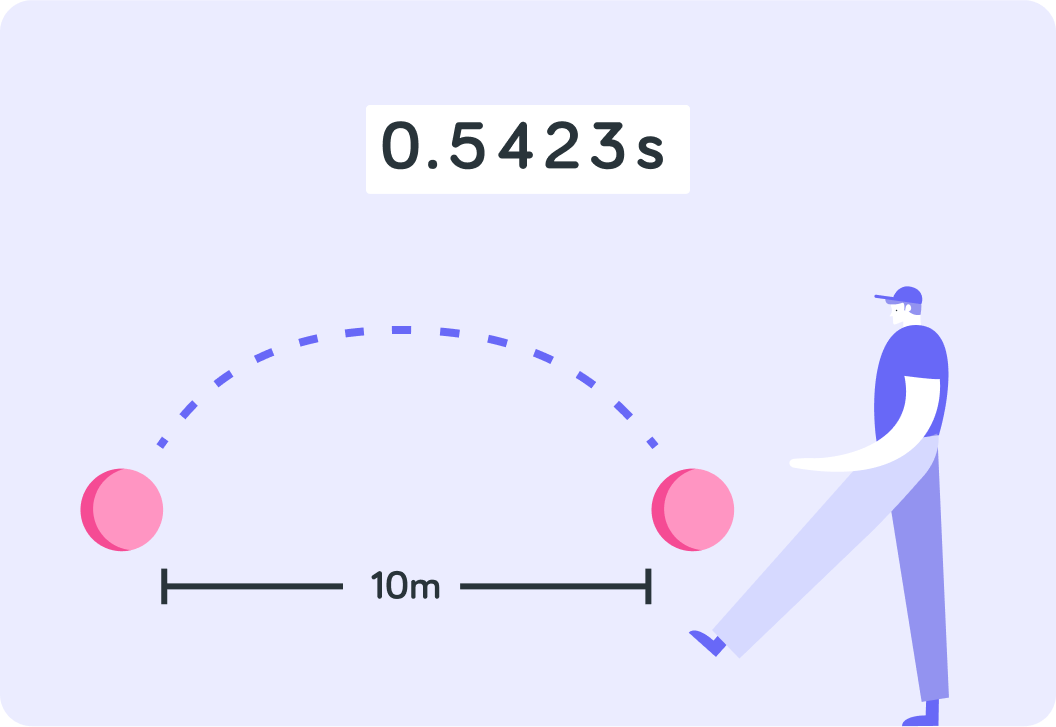
Imagine you measure how fast your friend can kick a football 10 metres

You start the stopwatch when you see his foot kick the ball. You stop the stopwatch when you see the ball cross the 10 metre line.

The stopwatch says $0.5423 \space s$ . Is it likely that your measurement is really that precise? Answer yes or no.

There is a lot of uncertainty in this measurement!

For example, your reaction time on the stopwatch will have affected the measurement, so you can't really say that it took exactly $0.5423 \space s$ for your friend to kick the ball 10 metres.

Would it be reasonable to say that it took about $0.5 \space s$ for your friend to kick the ball 10 metres? Answer yes or no.

$0.5 \space s$ has fewer significant figures, but is probably more "true" actually than $0.5423 \space s$

It doesn't pretend to be more precise than it necessarily is.

Recap! You might want to round off to fewer significant figures if the number doesn't have to be super precise

For example, whether it's a $1,820 \space km$ or a $1,800 \space km$ drive from London to Rome, probably isn't that significant.

You might want to round off to fewer significant figures if the number actually cannot be as precise as it appears

For example, you friend probably didn't kick a football 10 metres in exactly $0.5423 \space s$ . It's probably actually more "true" to simply say it took $0.5 \space s$

You might want to specify more significant figures to make it really clear that something does actually have to be very precise!

For example, if you give $152 \space cm$ to 5 SF like this $152.00 \space cm$ you are saying:

"It's not even $152.1 \space cm$ . It's actually exactly $152.00 \space cm$ !"

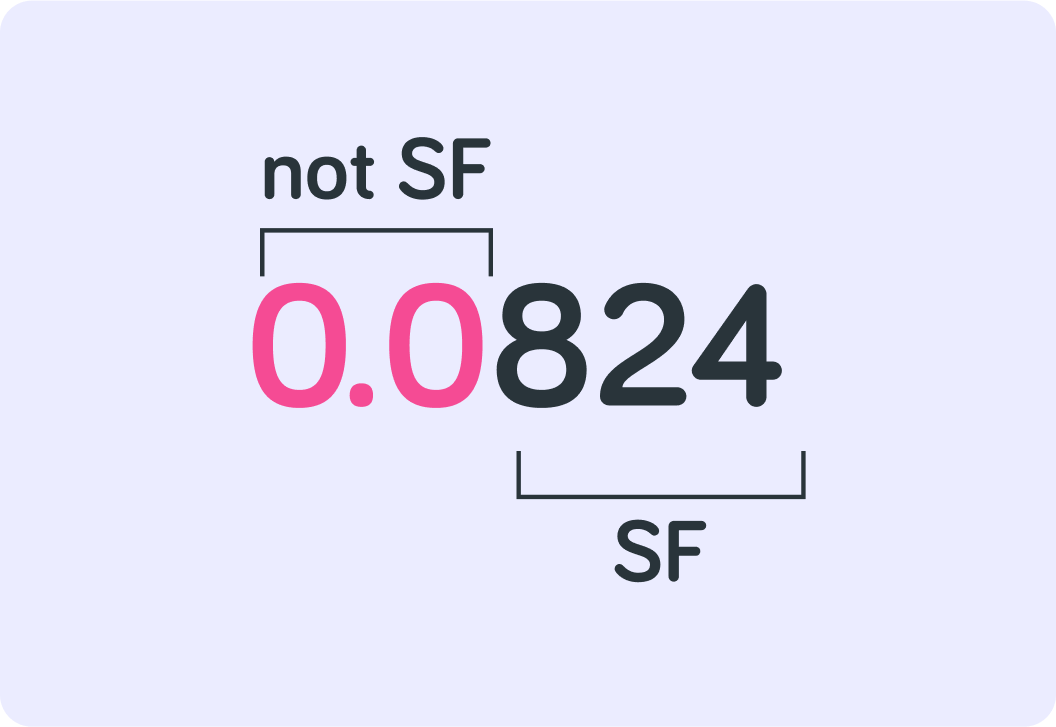
Significant figures start from the first non-zero figures in the number

So $0.0824$ has 3 SF. The zeros at the beginning of the number do not count!

Zeros at the end of whole numbers do not count as significant

So $759,324$ has 6 SF, whereas $759,000$ has only 3 SF.

However! Zeros after the decimal point do count as significant figures

So $759,000$ has only 3 SF, but $759,000.00$ has 8 SF!

Finally, zeros in-between significant figures count as significant too.

So the $0$ in $3,078.56$ is significant, so this number has 6 SF.

Now, $0.00456$ has only 3 significant figures. Which figures do you think are the significant ones?

How many significant figures are there in $9,607,845$ ?

How many significant figures are there in $62,840$ ?

How many significant figures are there in $0.0000045891$ ?

How many significant figures are there in $0.006078120$ ?

How do you actually round off numbers to a certain amount of significant figures?

Which number to 3 SF is $785,943$ closer to?

What about rounding off $5,712$ to 2 SF? Which number is $5,712$ closer to?

Now, what if you are exactly between two numbers, like rounding off $32,500$ to 2 SF. Do you think you round up or down?

So when you are exactly between two numbers you round up

For example, rounding off $32,500$ to 2 SF gives $33,000$ , not $32,000$

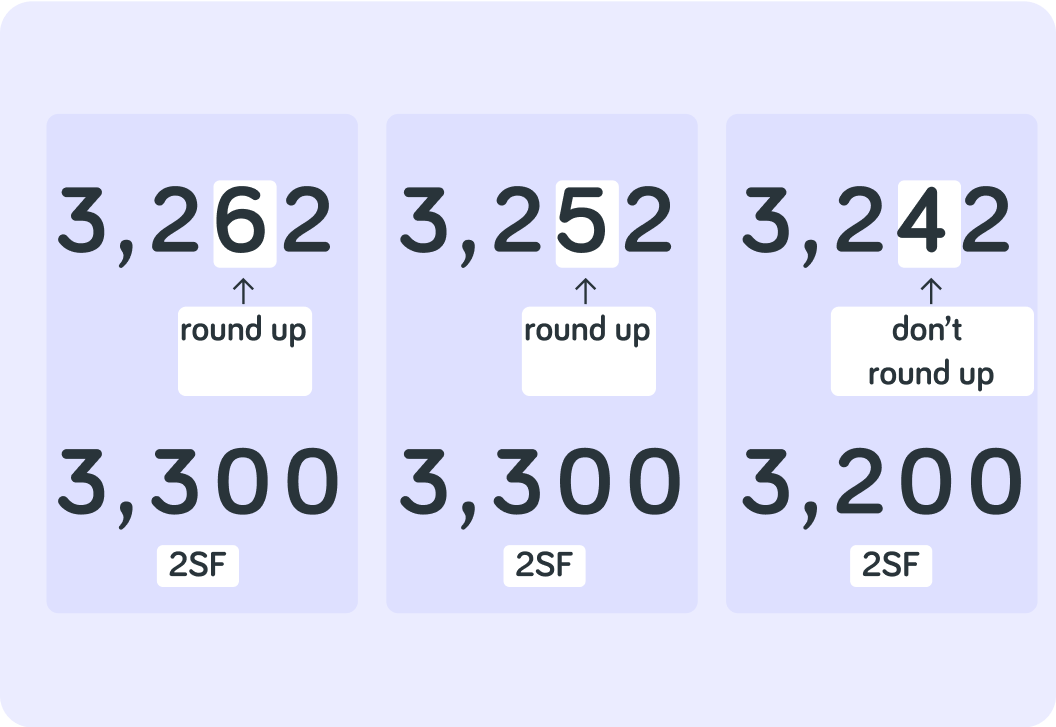
Recap! When you round off to for example 2 significant figures, you look at the figure that follows the 2nd significant figure

Then you decide if you need to round the 2nd significant figure up or if you should leave it.

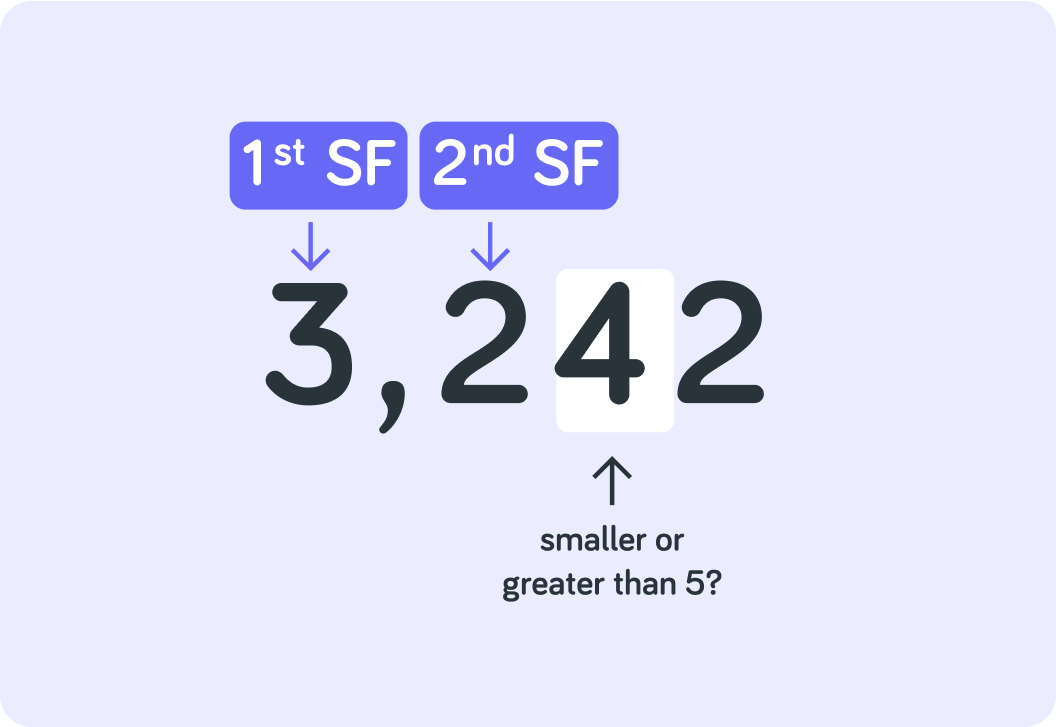
If the following figure is smaller than $5$ , you don't change the figure before it

So here, $3,242$ is rounded off to $3,200$ with 2 SF, not to $3,300$

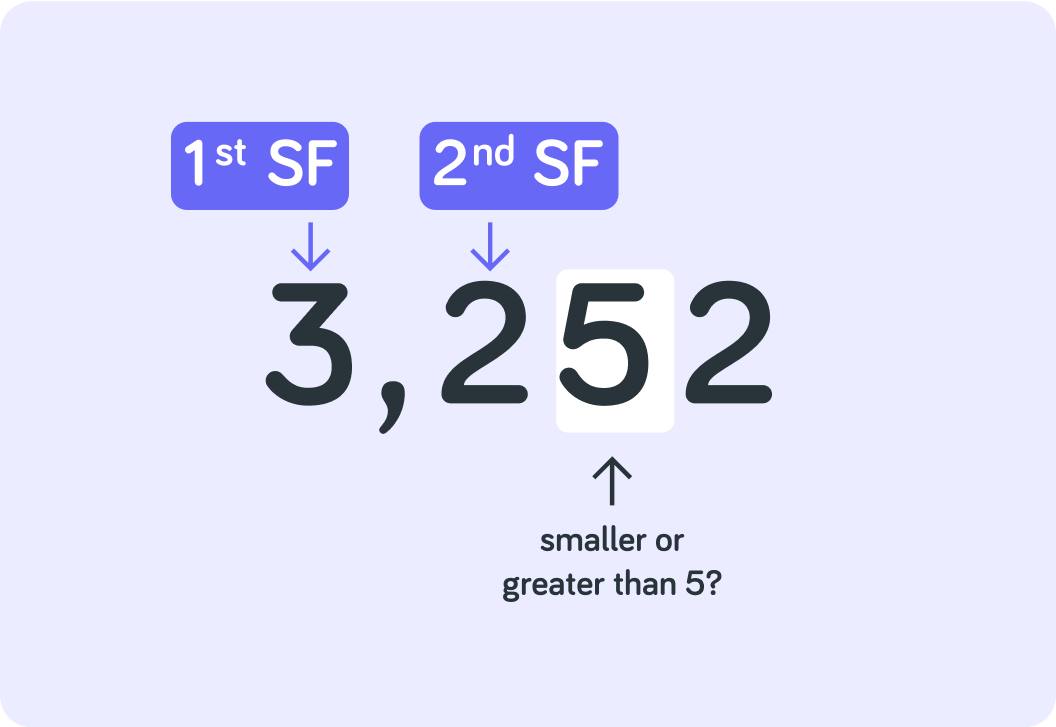
If the following figure is $5$ or greater than $5$ , you make the figure before it 1 bigger

So here, $3,252$ is rounded off to $3,300$ with 2 SF, not to $3,200$

Round $900.12$ to 3 SF.

Round $8,790,652$ to 1 SF.

Round off $0.00014512$ to 2 SF.

Summary! Significant figures (SF) are about how precise or exact a number is

The more significant figures, the more exact the number.

All zeros before a non-zero figure are never significant

For example, none of the zeros that come before the $6$ here count as significant, so this number has only 2 SF.

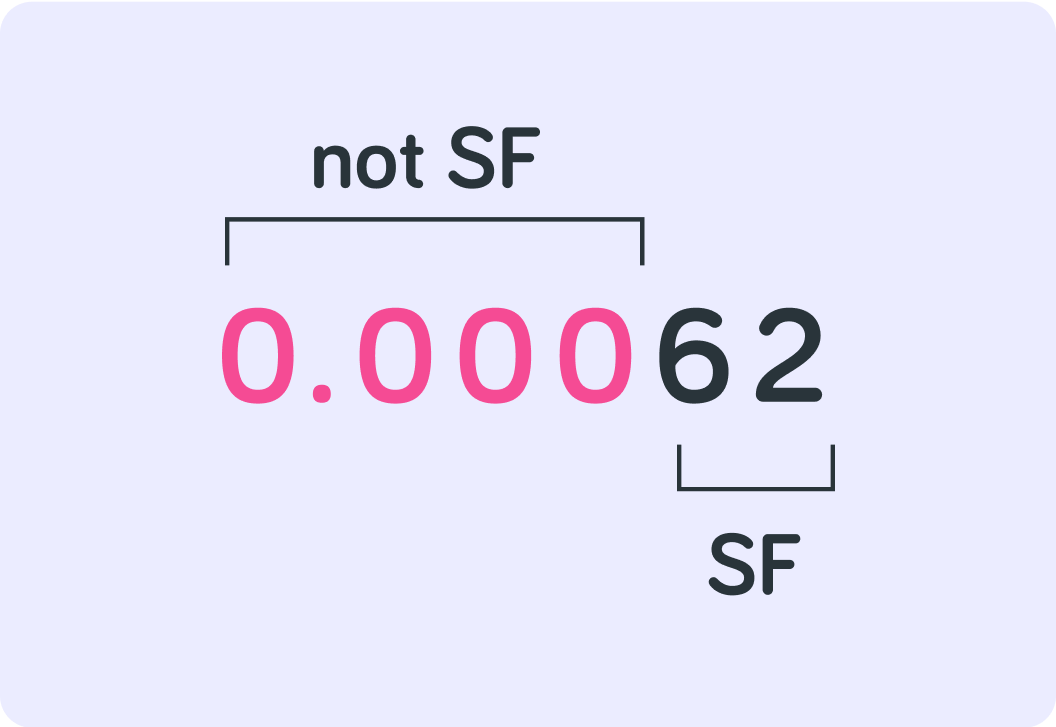
Zeros at the end of a whole number also don't count as significant

For example, the $0$ in $93,870$ is not significant, so $93,870$ has only 4 SF.

Zeros as decimals after whole numbers are significant though!

For example, all figures in $516.30$ are significant, which means this number has 5 SF.

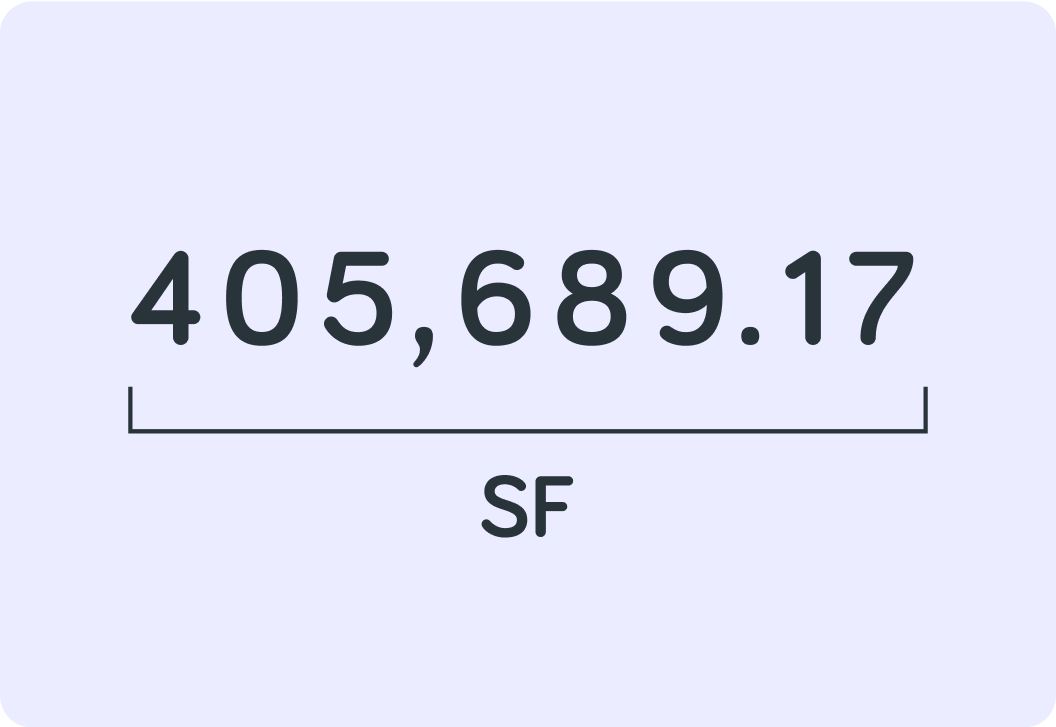
Zeros that are in-between significant figures always count as significant

For example, the $0$ in $405,689.17$ is significant, so this number has 8 SF.

When you round to significant figures, you need to look at the following figure

If the figure is smaller than $5$ , you don't round up. If the figure is equal to or greater than $5$ , you do round up.