Number

YOU ARE LEARNING:

Standard Form: Multiplying and Dividing

You can also multiply and divide numbers in standard form, so it's easier to calculate with really big or really small numbers.

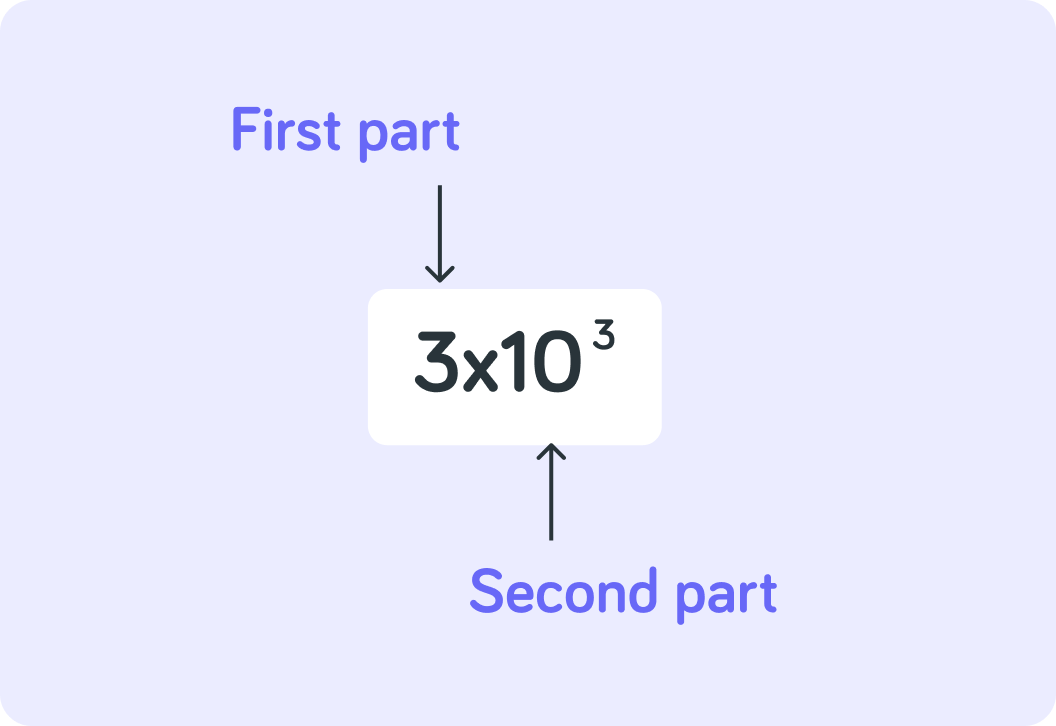
A number in standard form consists of two parts

A number between 1-10 and $10$ to some power.

Here are two numbers in standard form that should be multiplied

First have a look at what the numbers actually mean in non-standard form.

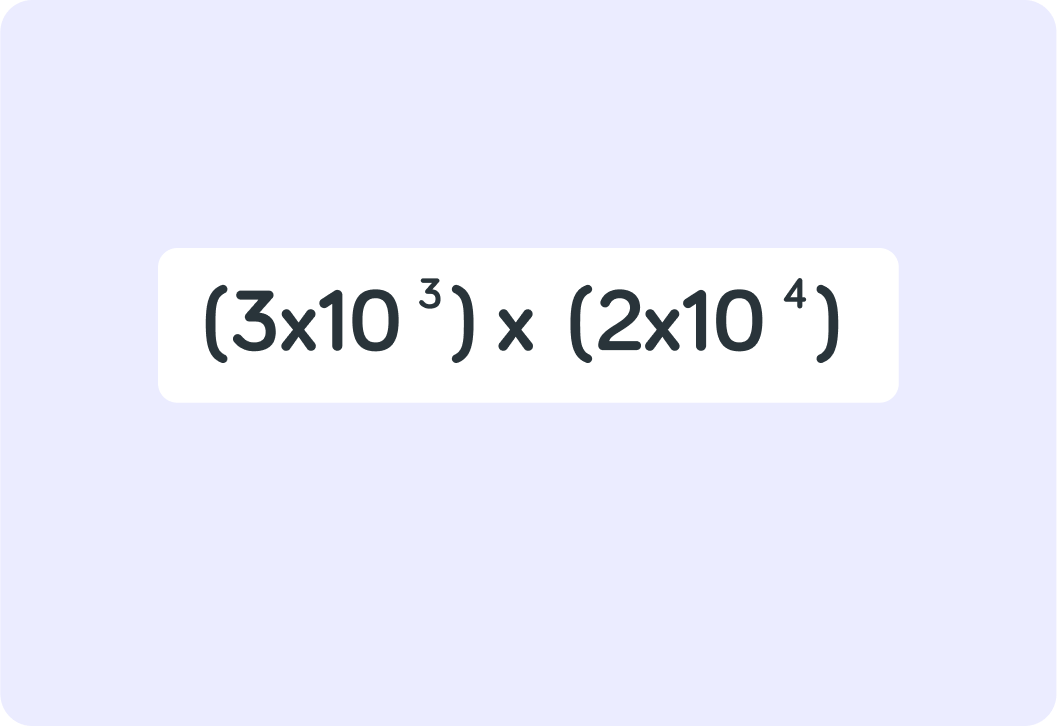
What is $3 \times 10^3$ in non-standard form?

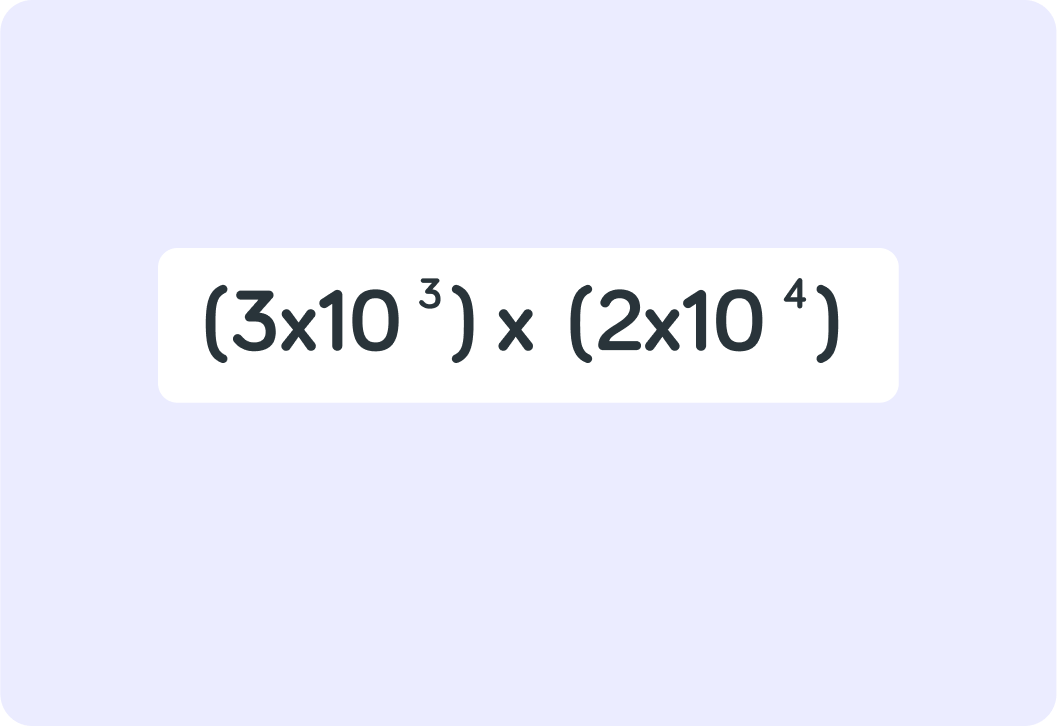
What is $2 \times 10^4$ in non-standard form?

So $(3 \times 10^3) \times (2 \times 10^4)$ ...

is the same as $3,000 \times 20,000$

Now, what is $3,000 \times 20,000$ ?

How do you write $60,000,000$ in standard form?

So $(3 \times 10^3)\times(2 \times 10^4) = 6 \times 10^7$

That is the same as $3,000 \times 20,000 = 60,000,000$ in non-standard form.

You don't have to change numbers into non-standard form first to multiply them

Take a look at this example.

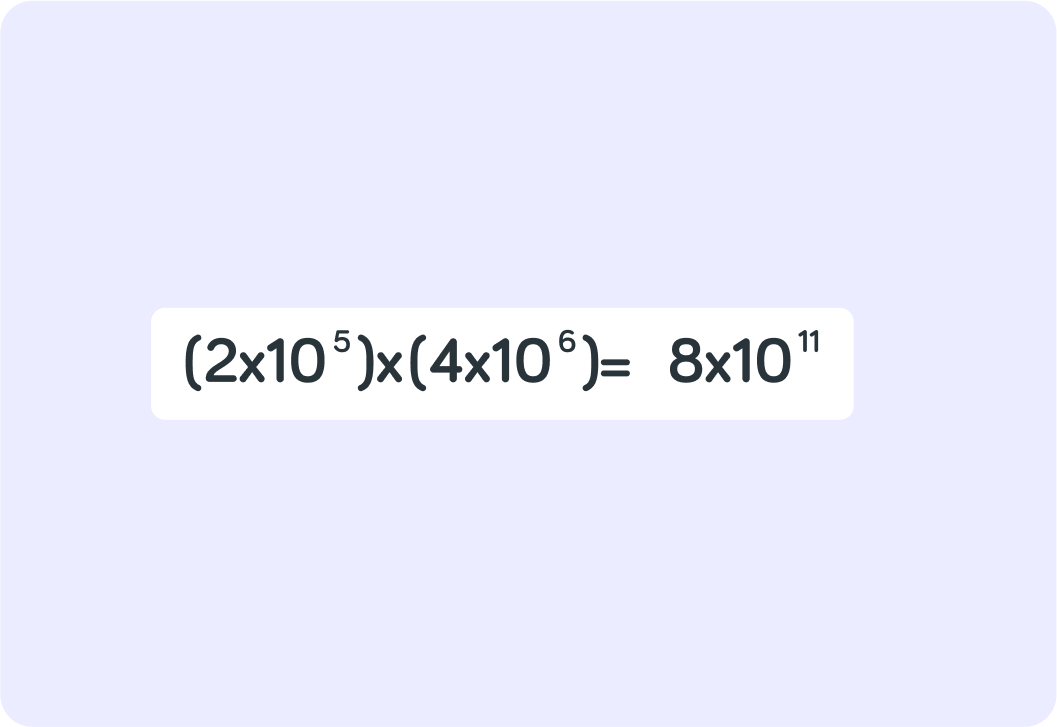
Where does the $8$ come from in the final result?

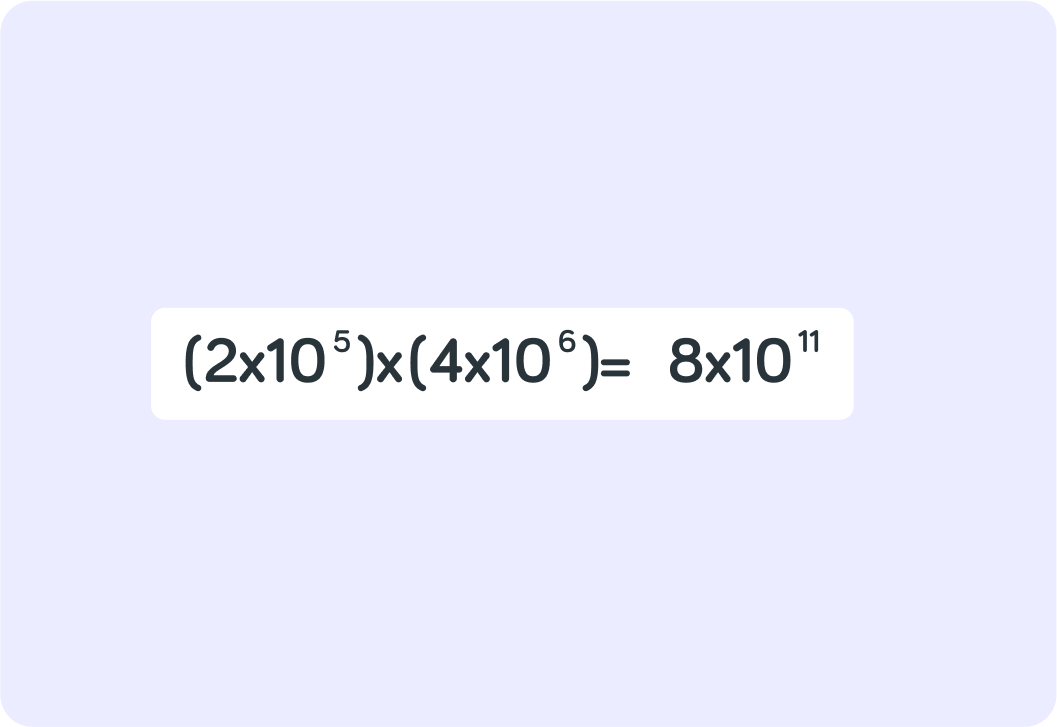
So you get to the first part of the result by multiplying the first part of the two numbers

Here that means $2 \times 4 =8$

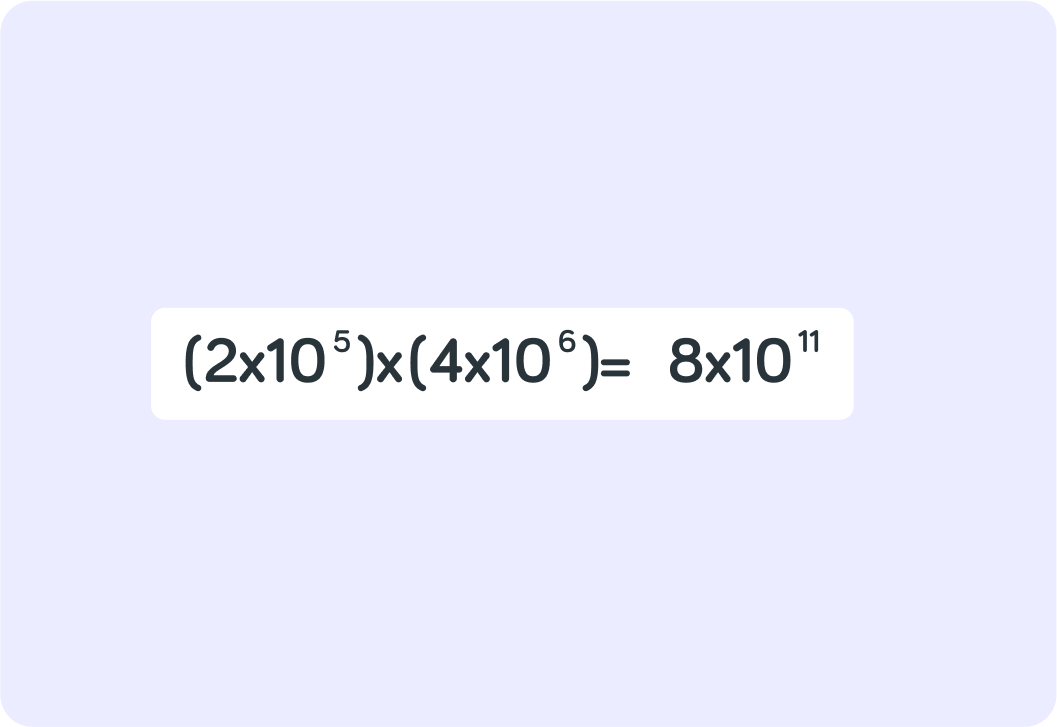
Where does $10^{11}$ come from in the final result?

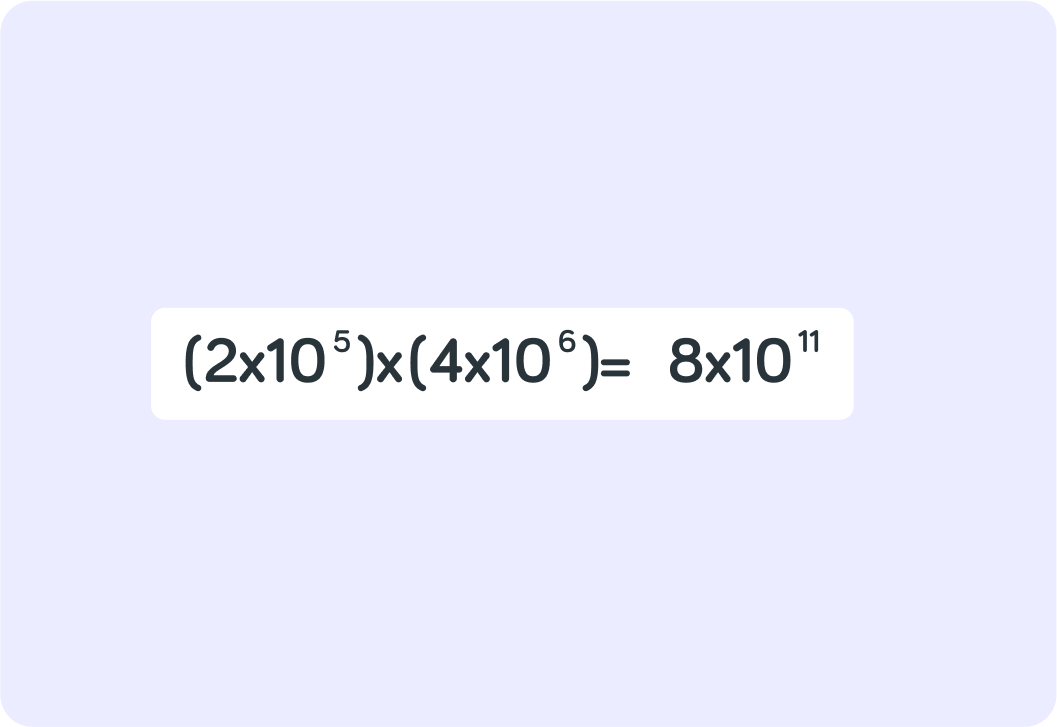
When you multiply indices, you actually add the powers together

So $10^5 \times 10^6 = 10^{11}$ is the same as saying $100,000 \times 1,000,000$

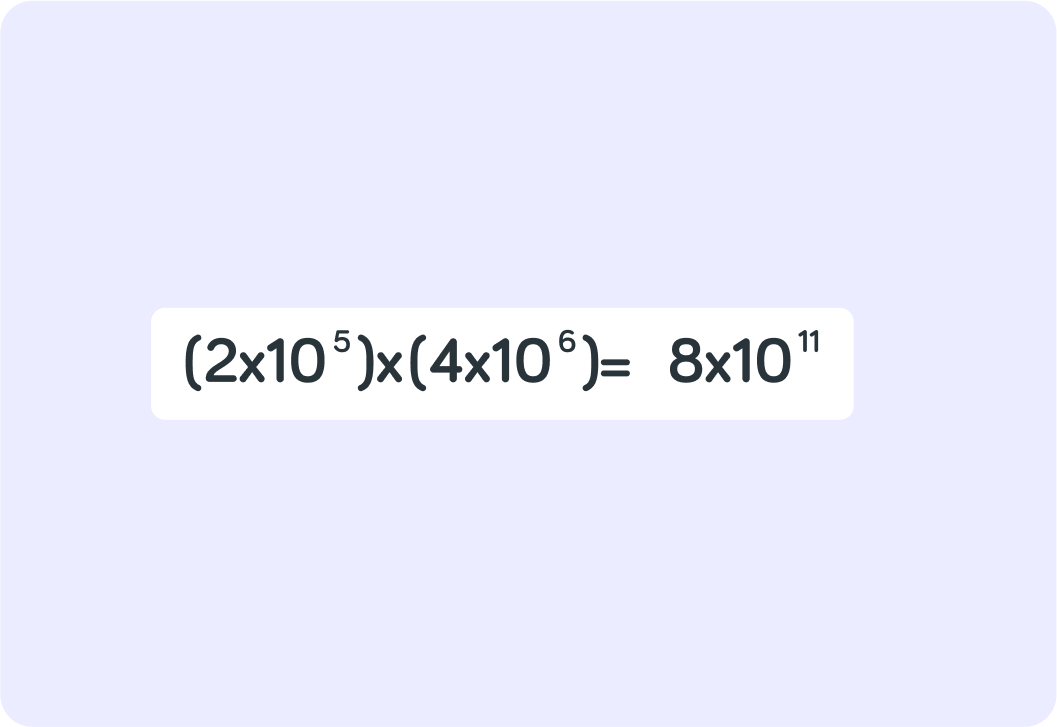
So now you have $8$ and $10^{11}$ . The last thing you need to do is to put them together with a __________

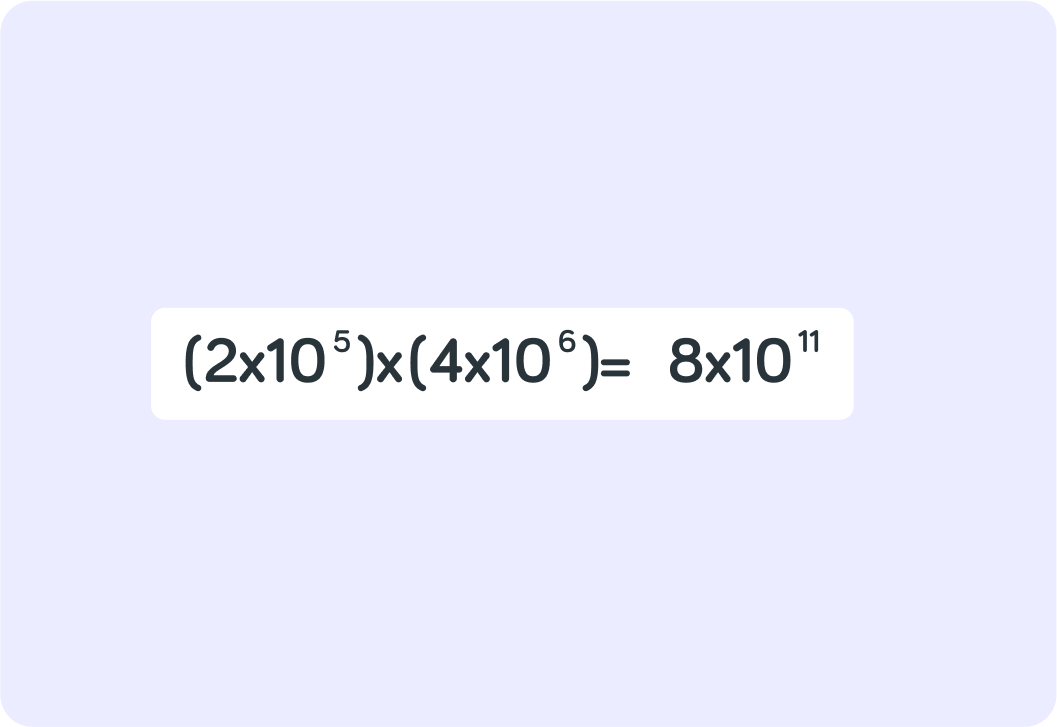
To recap! You multiply two numbers in standard form by first multiplying the first part of each number

Here that is $2 \times 4 = 8$

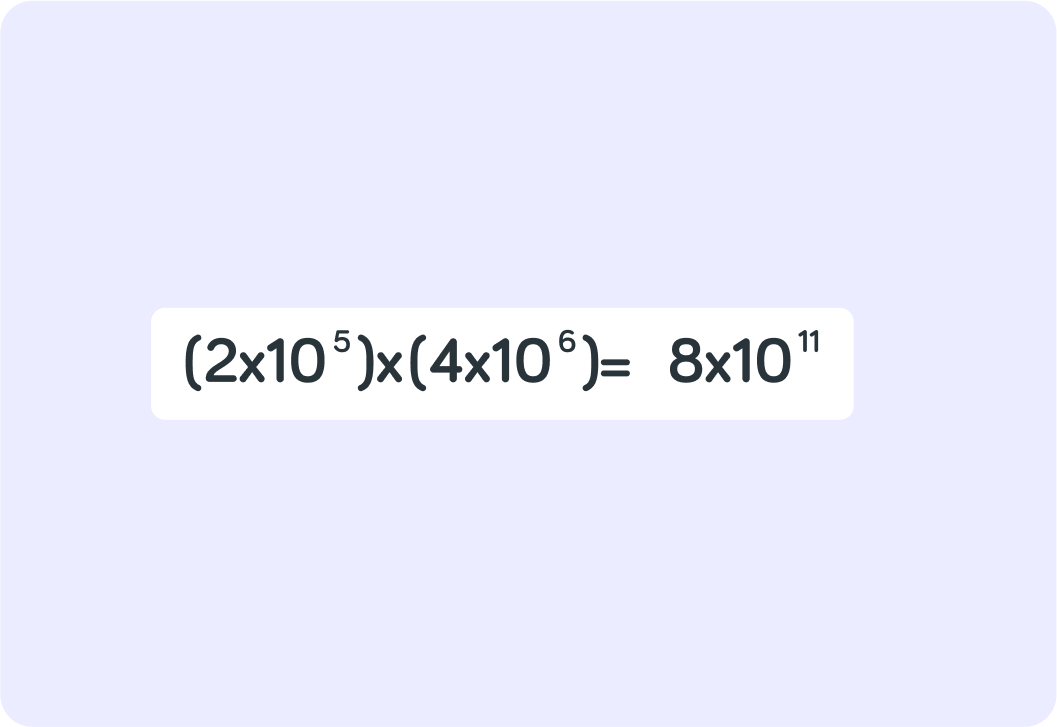
Then you multiply the second part of each number

When you multiply indices, you add the powers together, so here that is $10^5 \times 10^6=10^{11}$

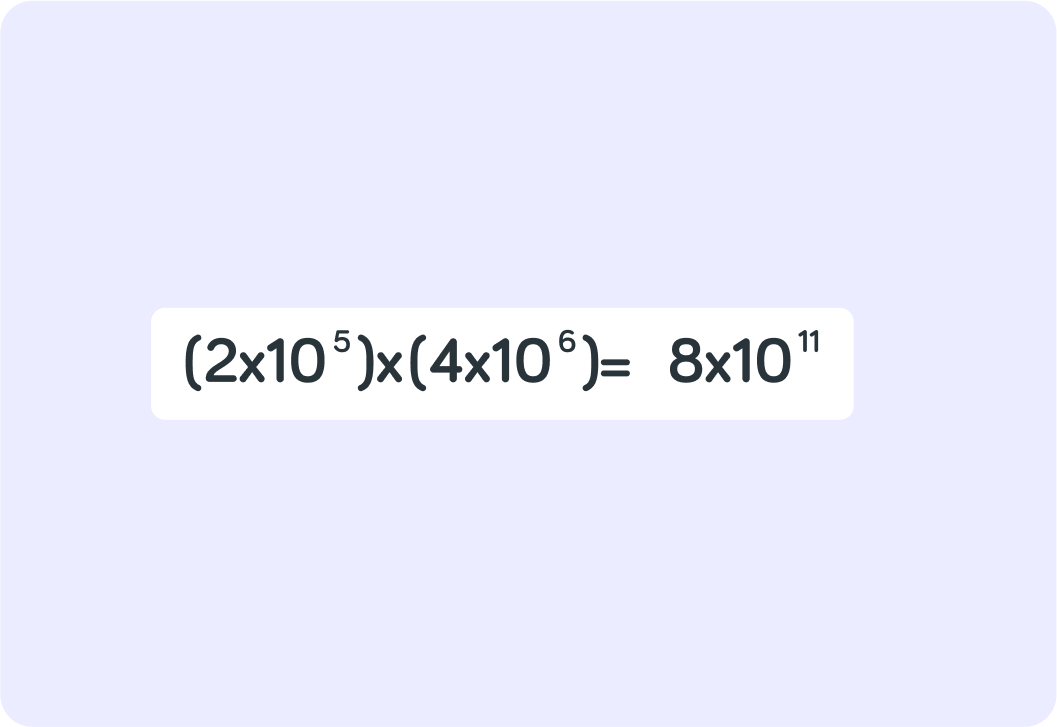
Finally, you combine the two parts in the result with a multiplication sign

So $8 \times 10^{11}$

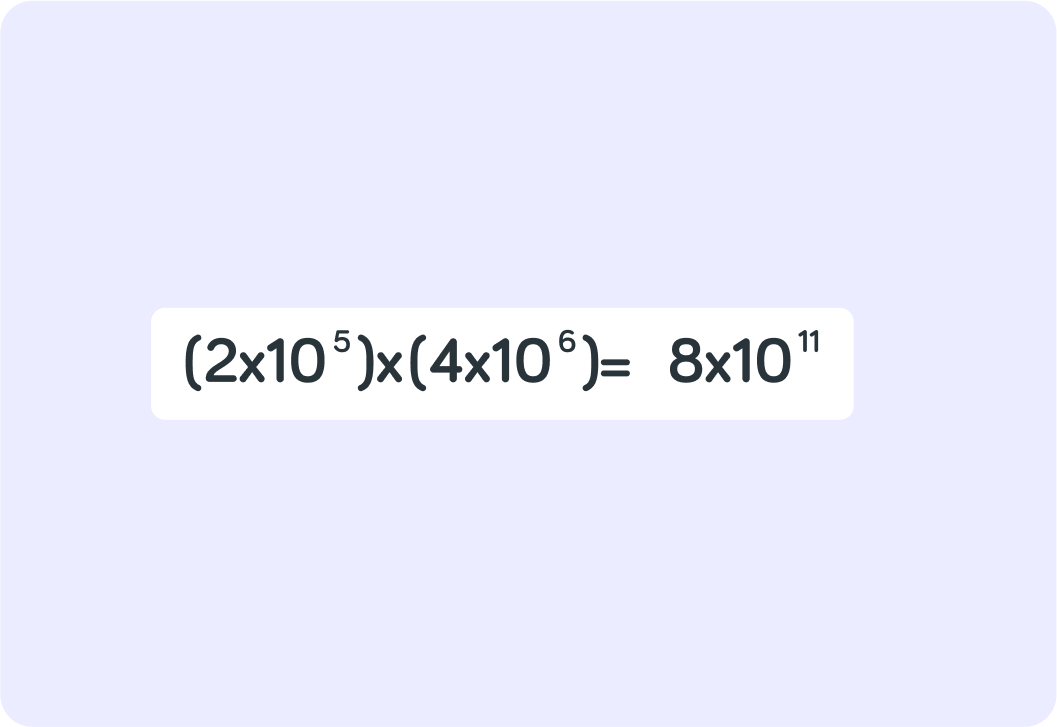
Now! The first part in standard form must be a number between 1-10!

So in this example, $12 \times 10^{10}$ is not a correct result.

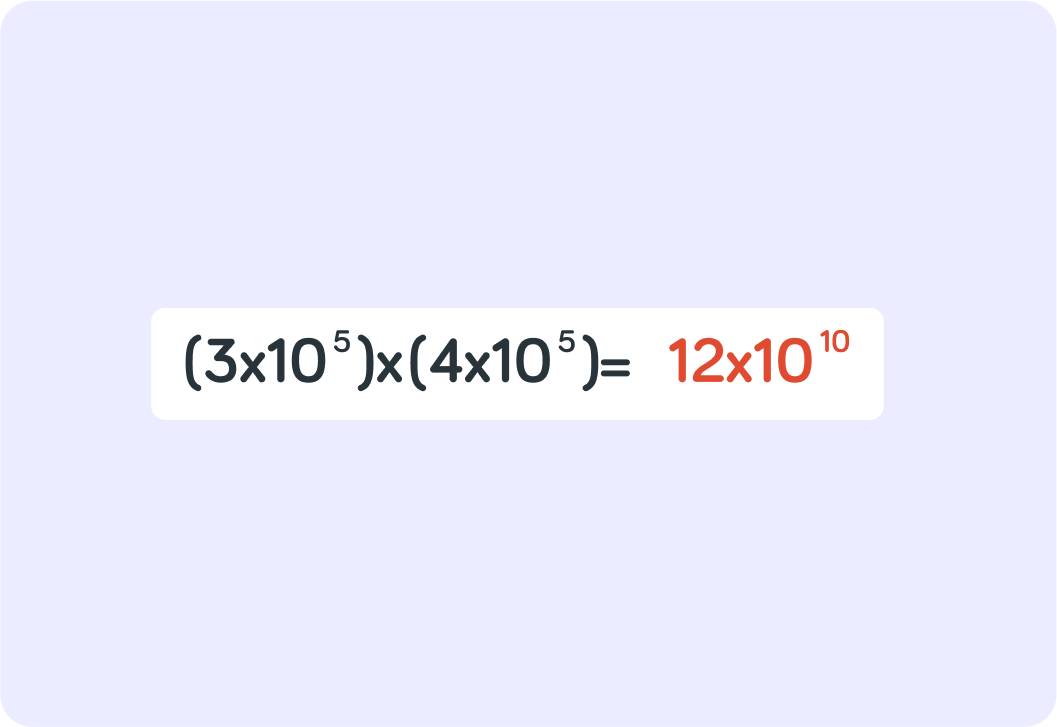
You can change $12$ to $1.2$ , but what do you then need to change $10^{10}$ to to make up for it?

You can change $12$ to $1.2$ to make sure you have a number between 1-10

But that means you have to make $10^{10}$ 10 times larger to make up for it. That gives you $10^{11}$

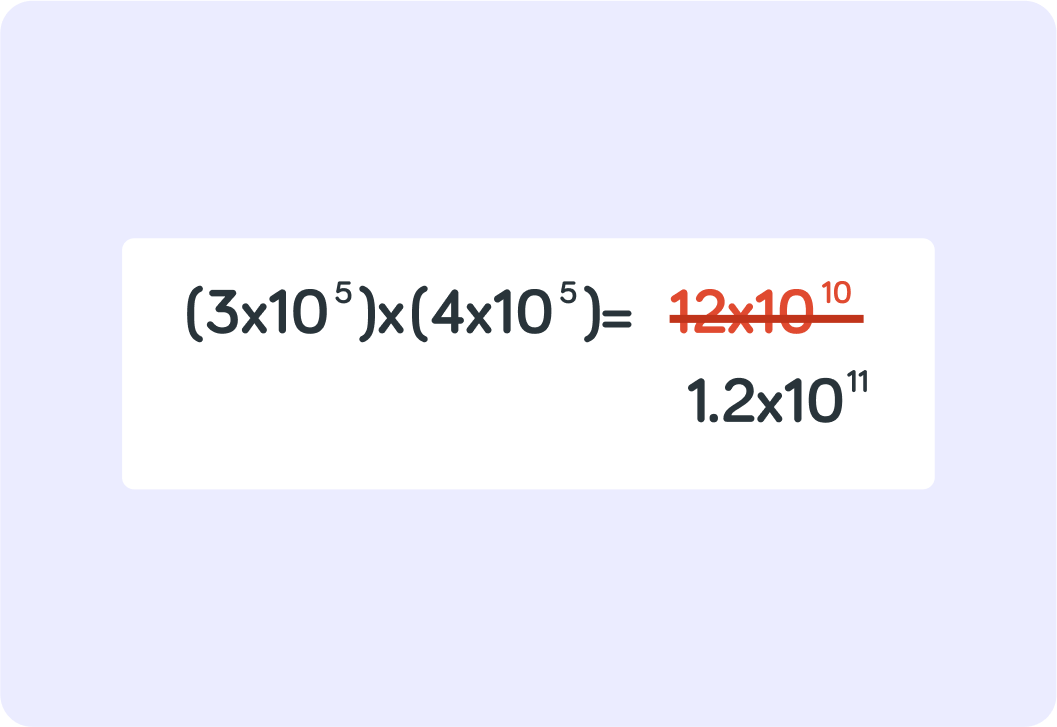
What is $(4 \times 10^6)\times (1.5 \times 10^3)$ ? Give your answer in standard form.

What is $(3 \times 10^6)\times (5\times 10^7)$ ? Give your answer in standard form.

Here the two numbers in standard form should be divided, not multiplied

How do you do that then?

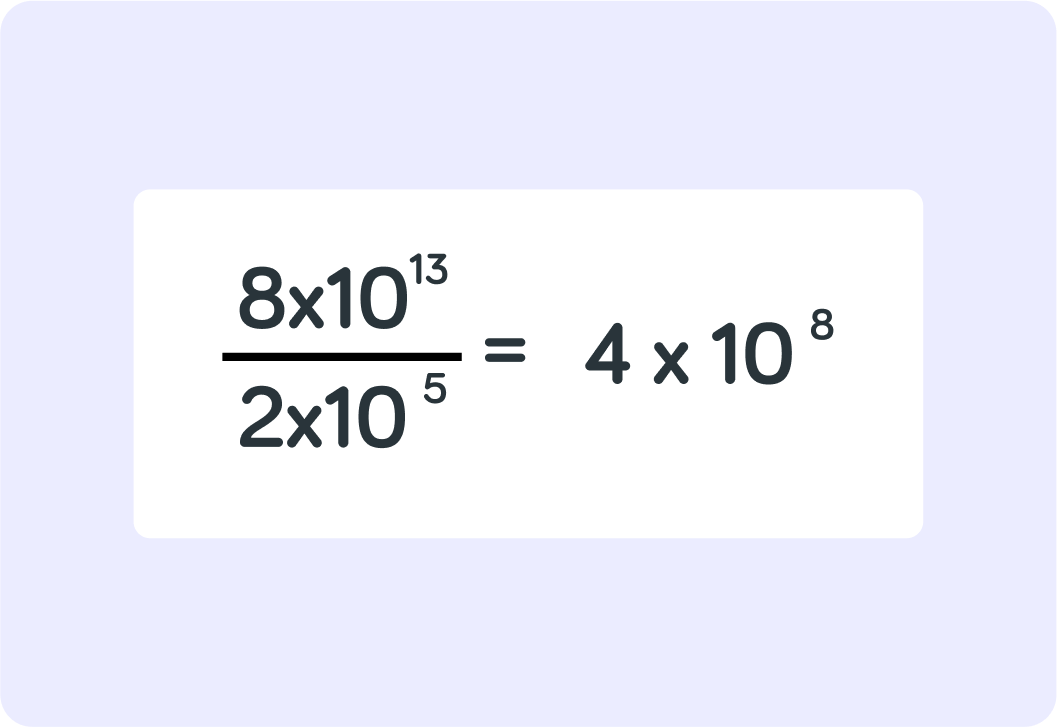
What do you do with the first part of the numbers?

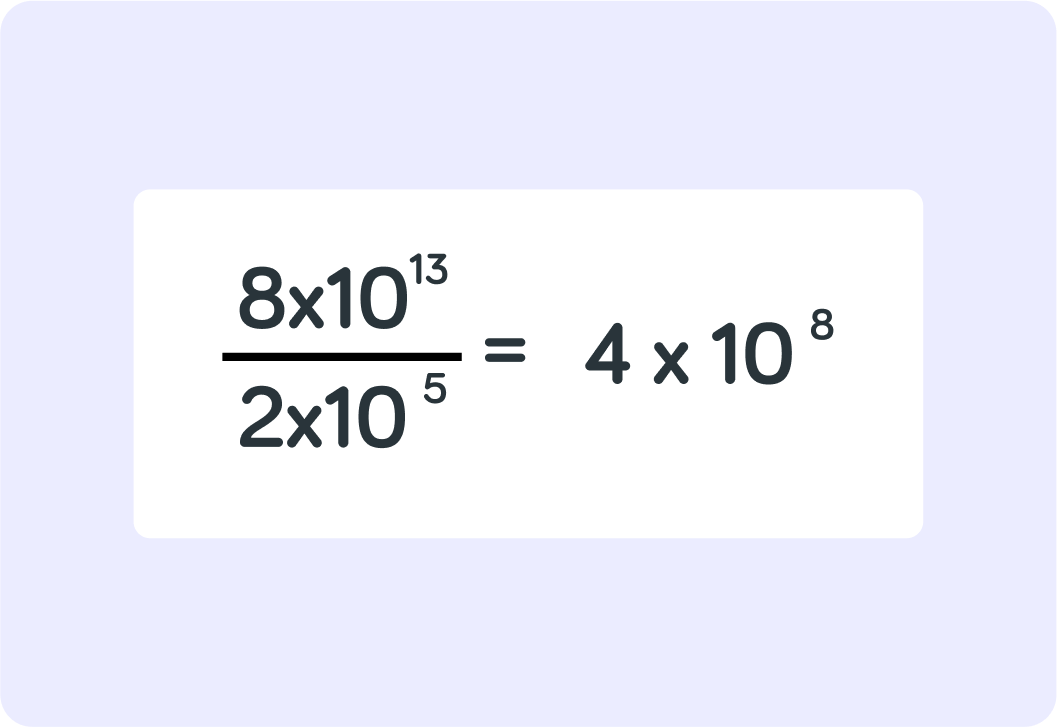
What do you do to divide the indices in the second part of the numbers?

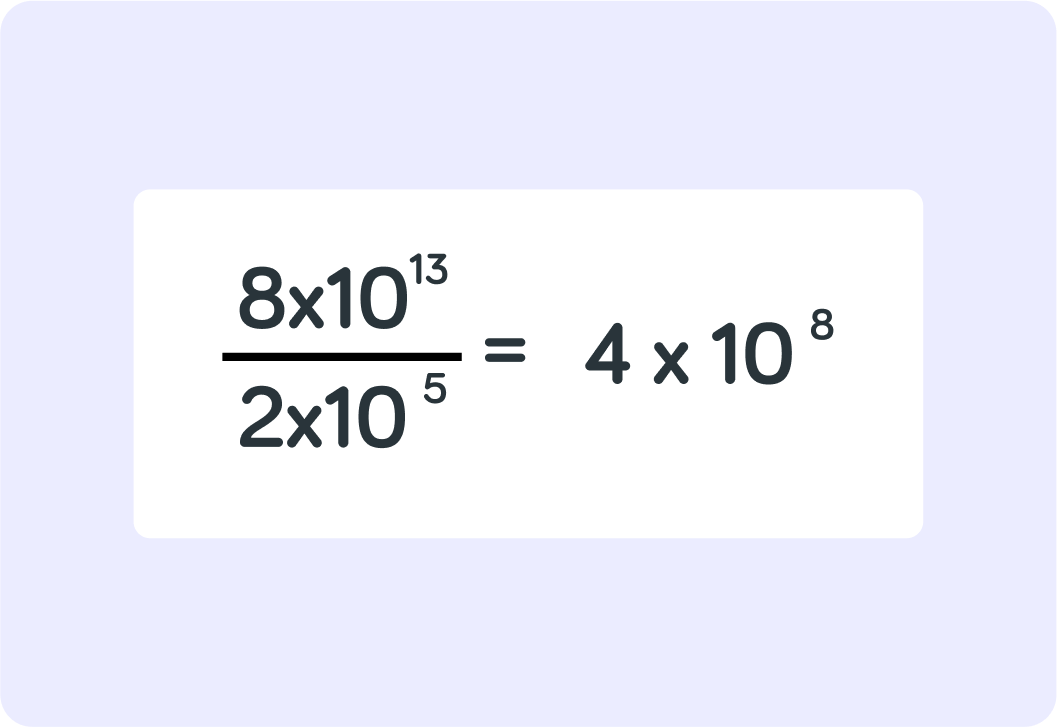
So to divide numbers in standard form, you do the opposite of what you would do to multiply them.

You divide the first parts. You subtract the powers in the indices in the second part.

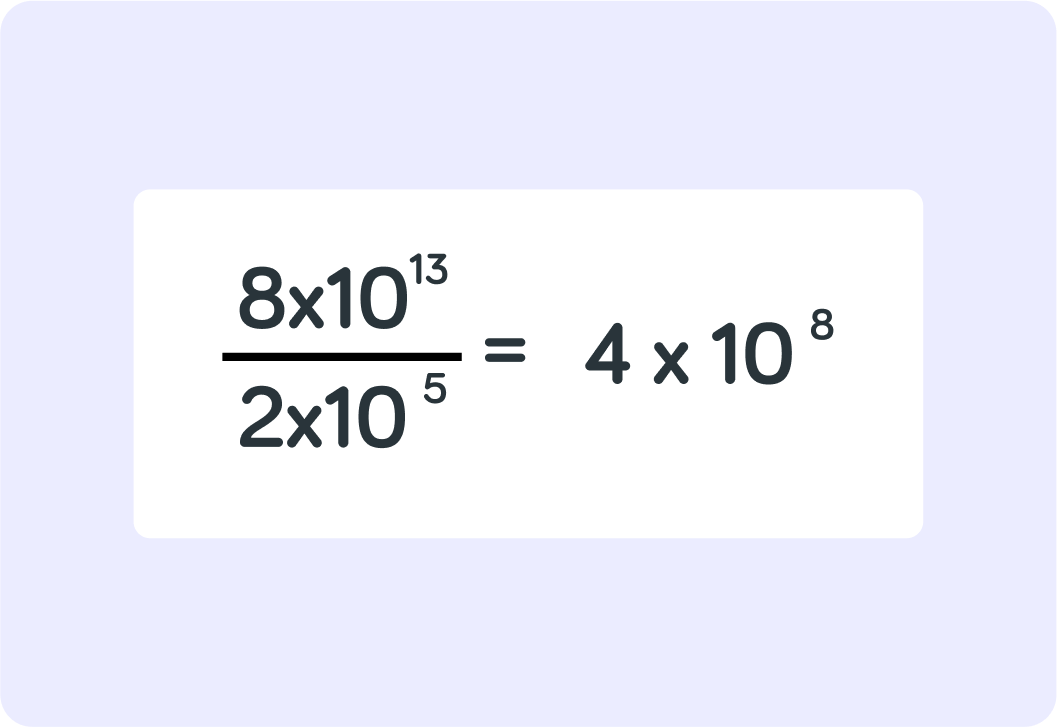
Now! The first part in standard form must be a number between 1-10!

So in this example, $0.5\times10^5$ is not a correct result.

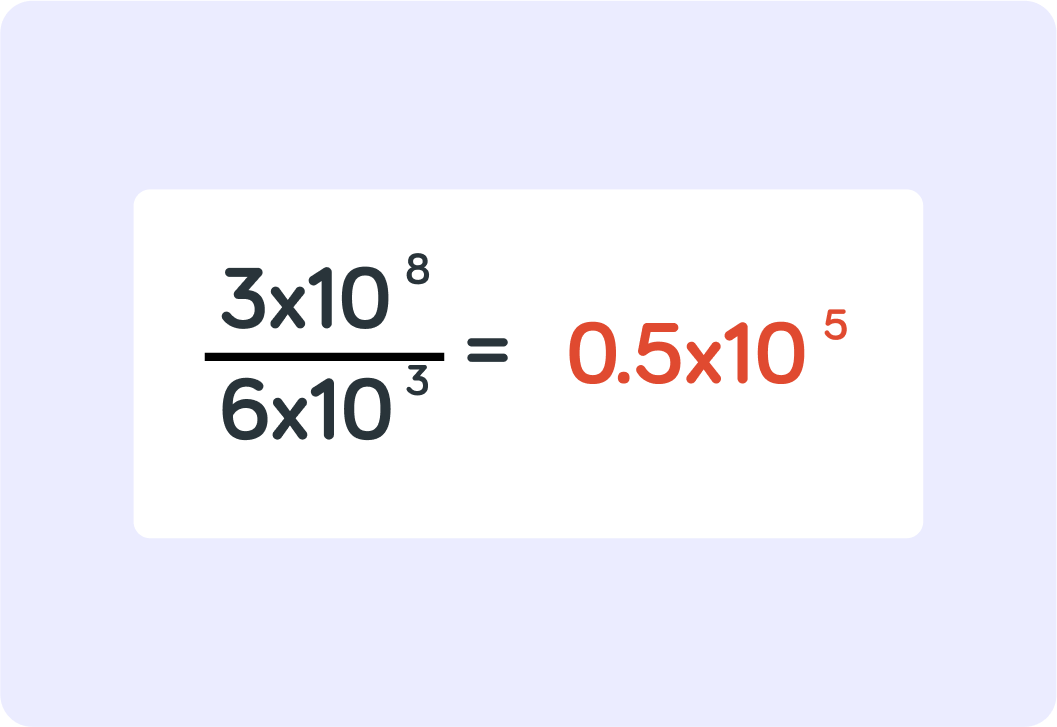
You can change $0.5$ to $5$ , but what do you then need to change $10^5$ to to make up for it?

A) $10^4$ B) $10^6$

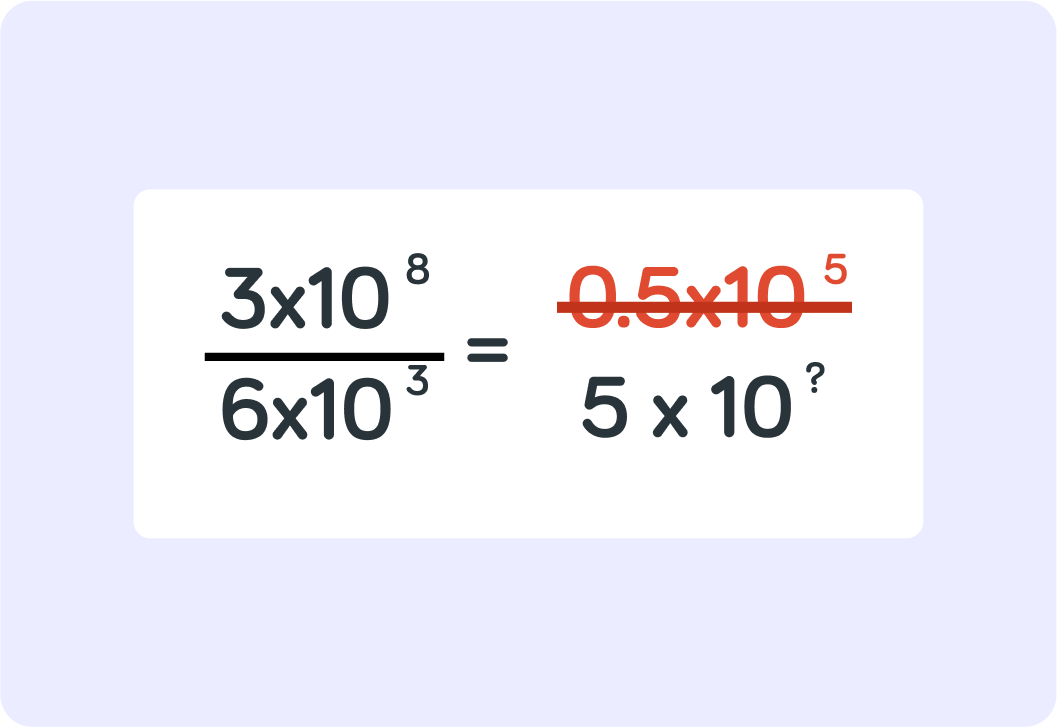
You can change $0.5$ to $5$ , but what do you then need to change $10^5$ to to make up for it?

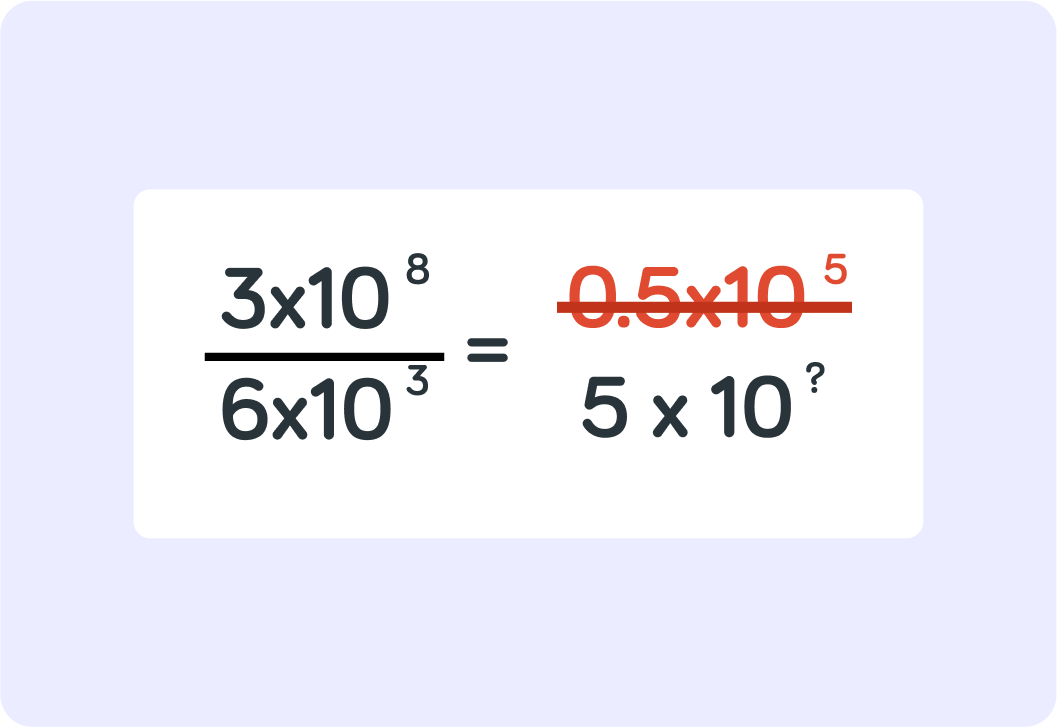
You can change $0.5$ to $5$ to make sure you have a number between 1-10

But that means you have to make $10^5$ 10 times smaller to make up for it. That gives you $10^4$

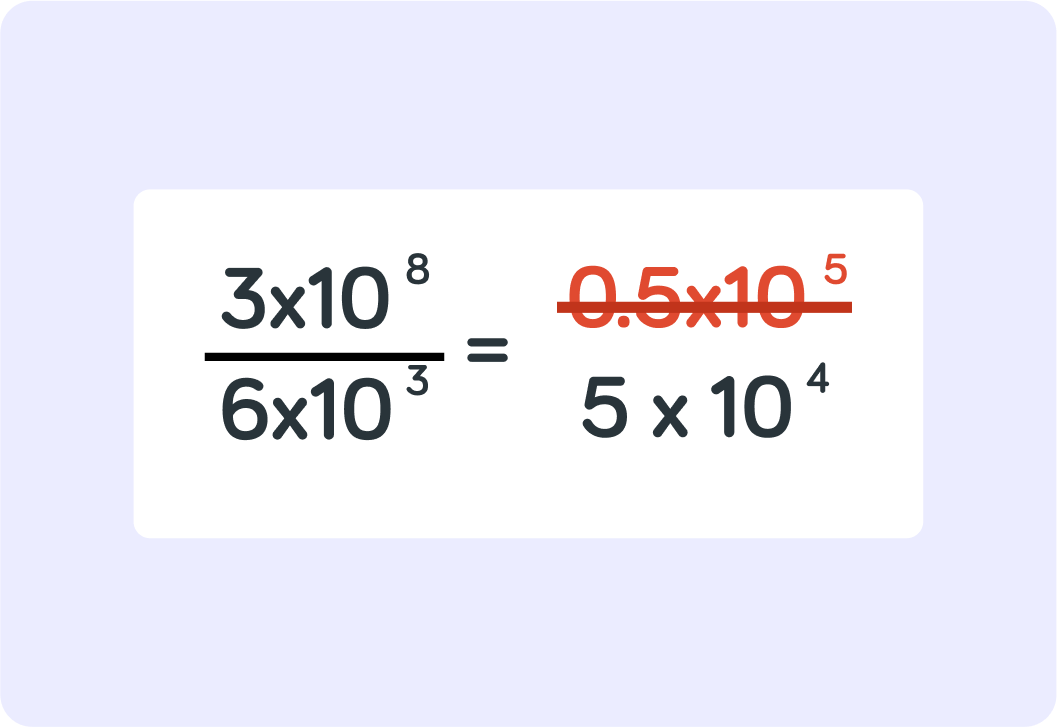
What is $\frac{9\times10^{11}}{3\times10^4}$ ? Give your answer in standard form.

What is $\frac{2\times10^9}{8\times10^3}$ ? Give your answer in standard form.

Summary! You can multiply numbers in standard form without changing them into non-standard form first

First you multiply the first parts. Then you multiply the indices by adding the powers. Finally you combine the results with a multiplication sign.

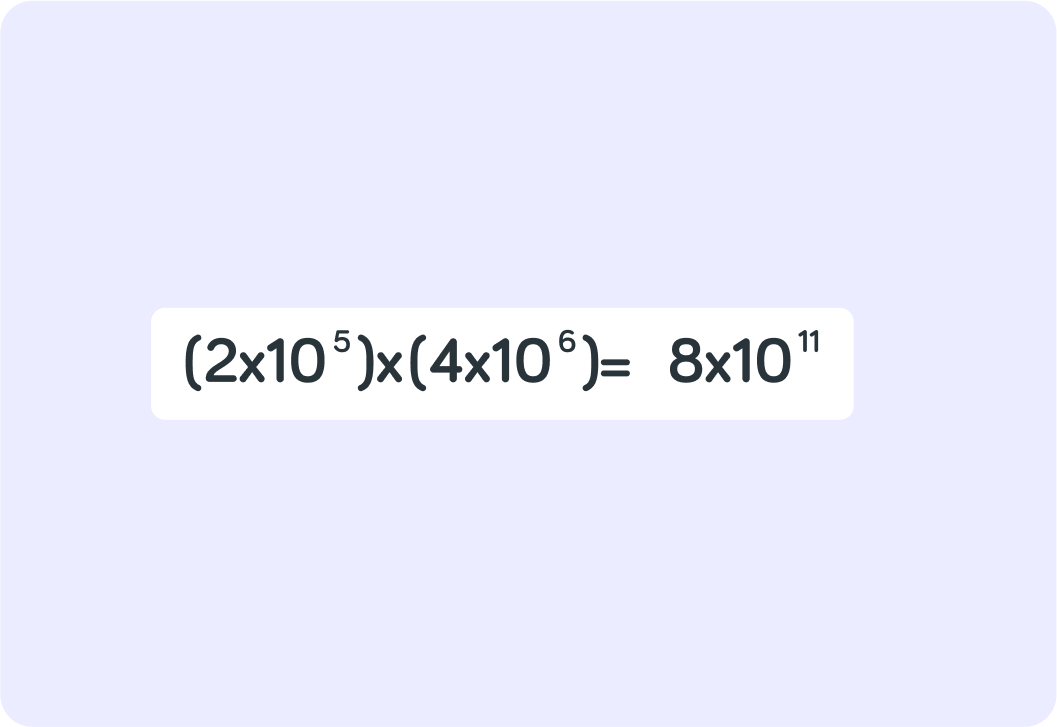
You can also divide numbers in standard form

First you divide the first parts. Then you divide the indices by subtracting the powers. Finally you combine the results with a multiplication sign.

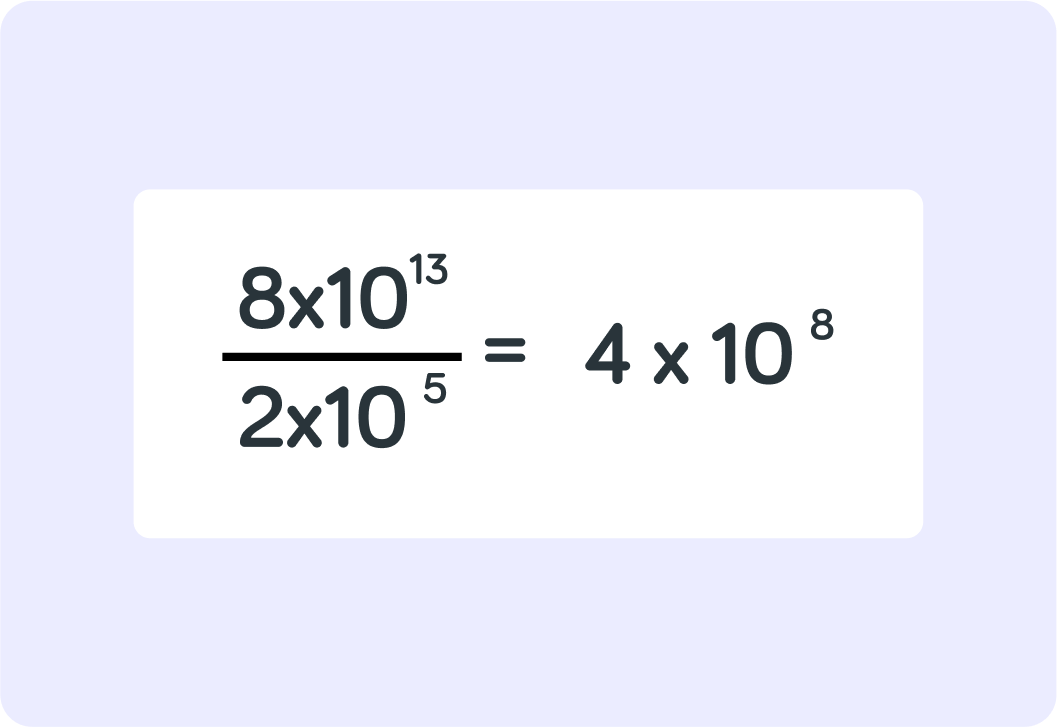
Remember that the first part has to be a number between 1-10

You might have to make the first part either 10 times bigger or 10 times smaller.

Then you have to make the index 10 times smaller or 10 times bigger to make up for it.