Albert Teen

powered by

GCSE Exam Guide Parent

>

>

>

What are percentages

Number

YOU ARE LEARNING:

What Are Percentages?

What Are Percentages?

lesson introduction

What Are Percentages?

Percentages are a useful way to represent amounts. You can convert between fractions, decimals and percentages.

1

How many little blocks do you see here?

block image

2

Now, how many of the blocks have been coloured in?

block image

3

So $\frac{37}{100}$ blocks have been coloured in

This is the same as 37 percent of the blocks.

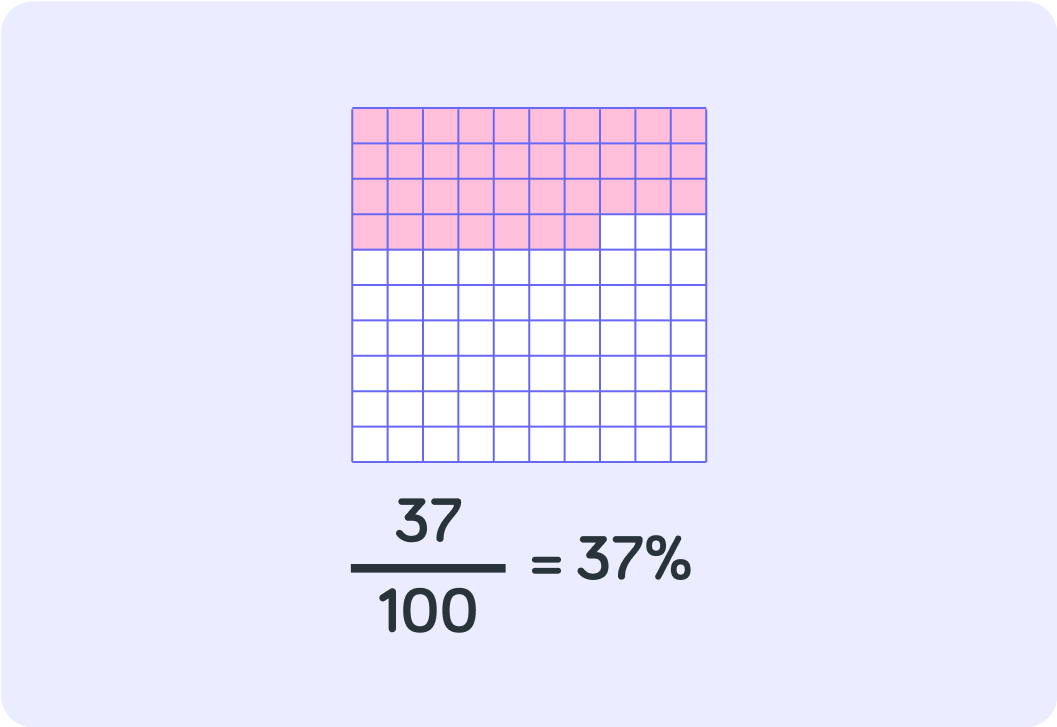
block image

How can you also write 37 percent?

1

What does "percent" $\%$ actually mean?

Where else do you know "cent" from?

block image

2

How many centimetres are there in a metre?

block image

3

How many years are there in a century?

block image

4

How many centilitres are there in a litre?

block image

5

So "percent" means "per _________".

A) $10$ B) $100$ C) $1000$

block image

6

"Percent" means "per 100"

So when you say $37\%$ , you actually say "37 out of 100" or $\frac{37}{100}$

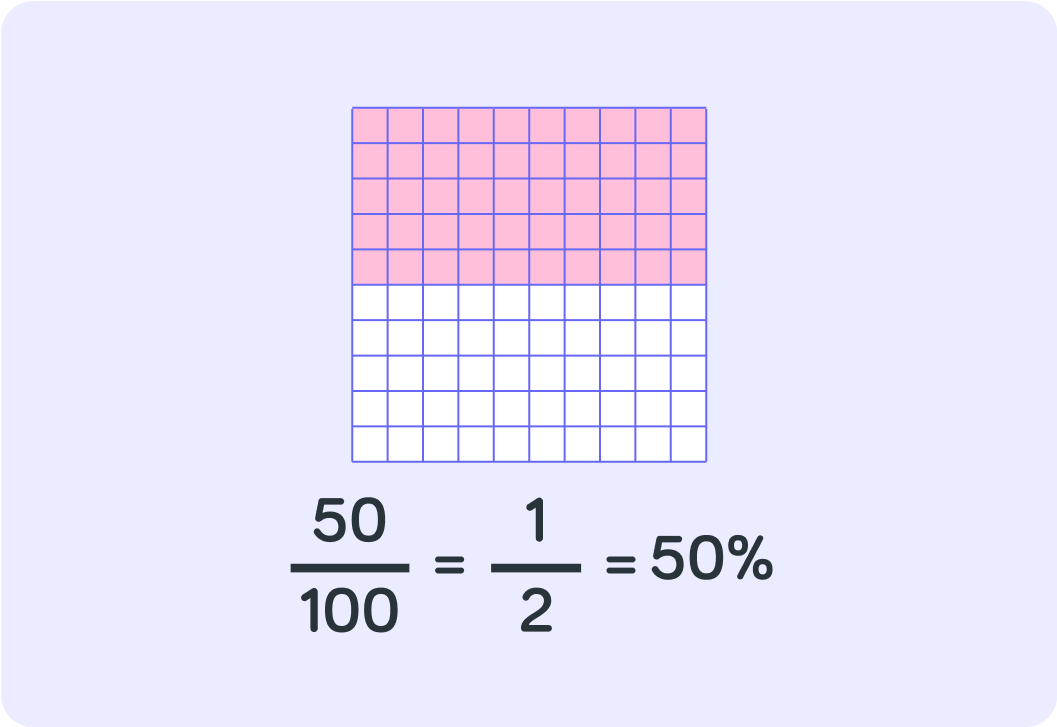
block image

1

How many $\%$ of these blocks have been coloured in?

block image

2

$\frac{50}{100}$ or $50\%$ of these blocks have been coloured in. What does the fraction $\frac{50}{100}$ become when it has been simplified as much as possible?

block image

3

So $50\%$ is the same as $\frac{50}{100}$ which is the same as $\frac{1}{2}$

Half of these blocks are coloured in.

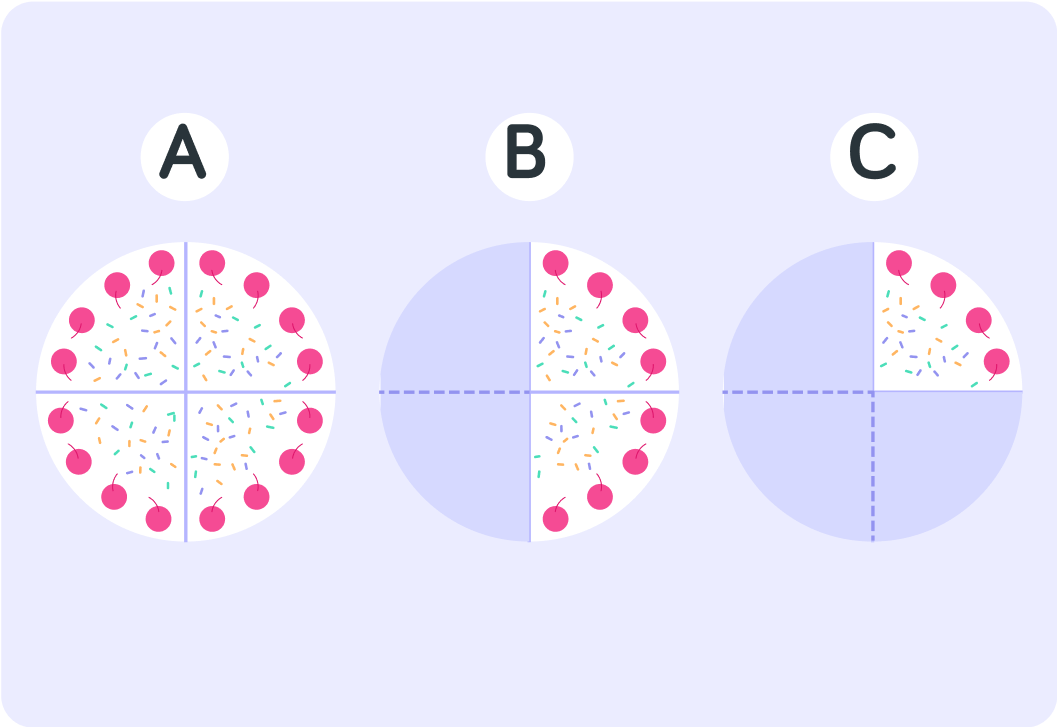
block image

1

Now, which one of these cakes shows that only $50\%$ is left? Answer A, B or C.

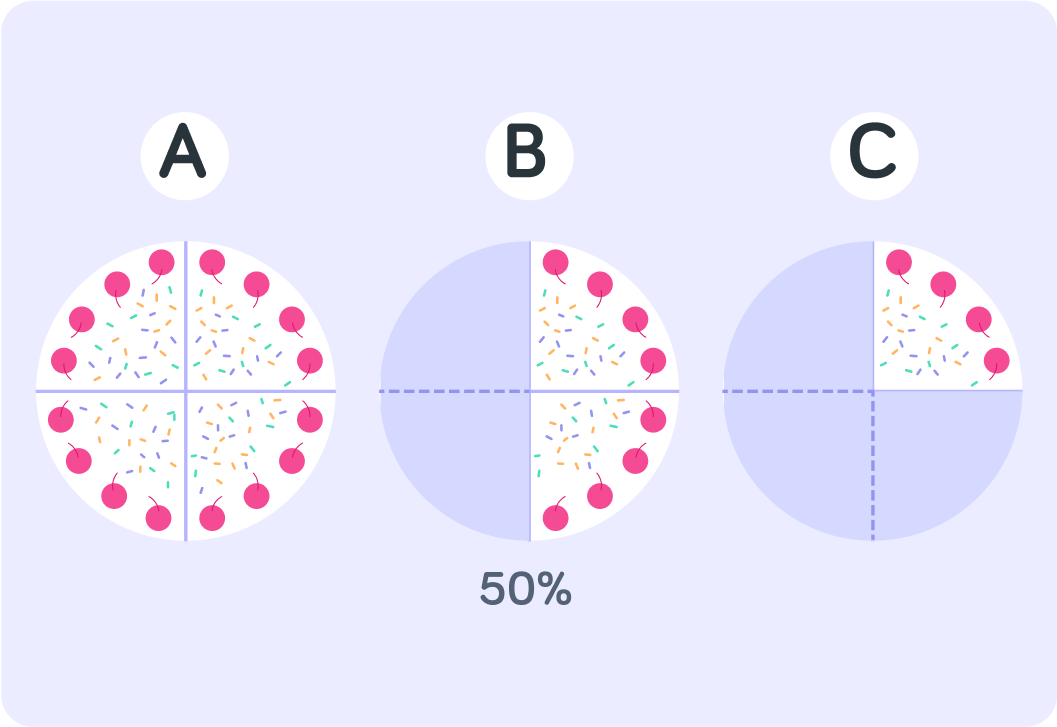
block image

2

Which cake shows that only $25\%$ is left? Answer A, B or C.

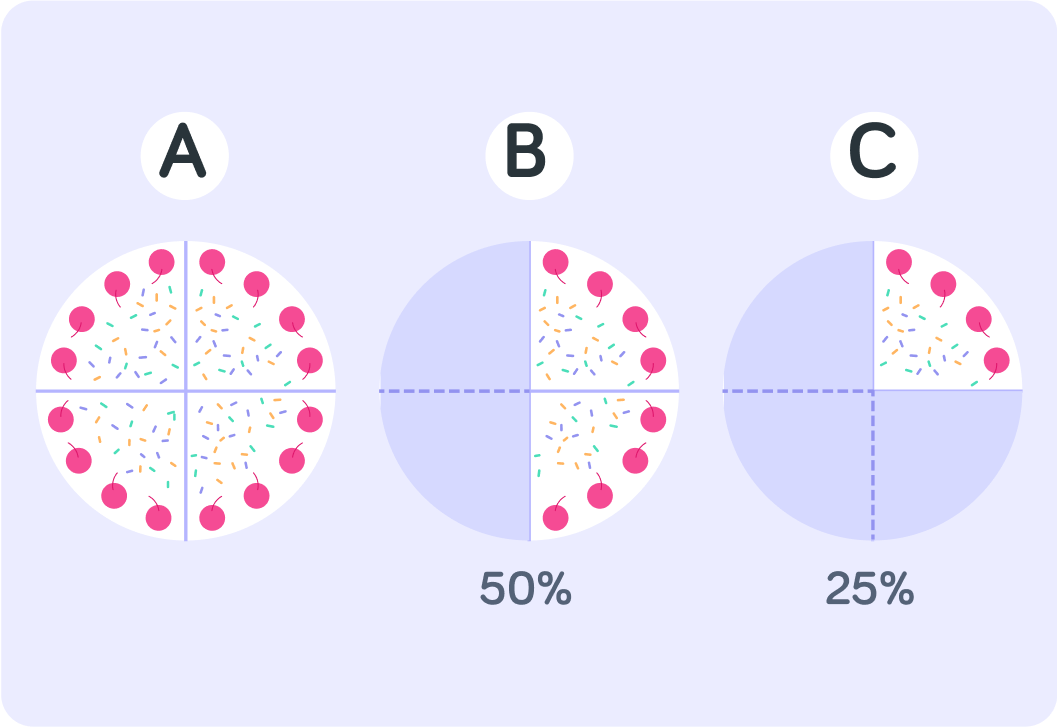
block image

3

Which cake shows that $100\%$ is left? Answer A, B or C.

block image

4

So what is $100\%$ the same as?

A) $1$ B) $100$ C) $0$

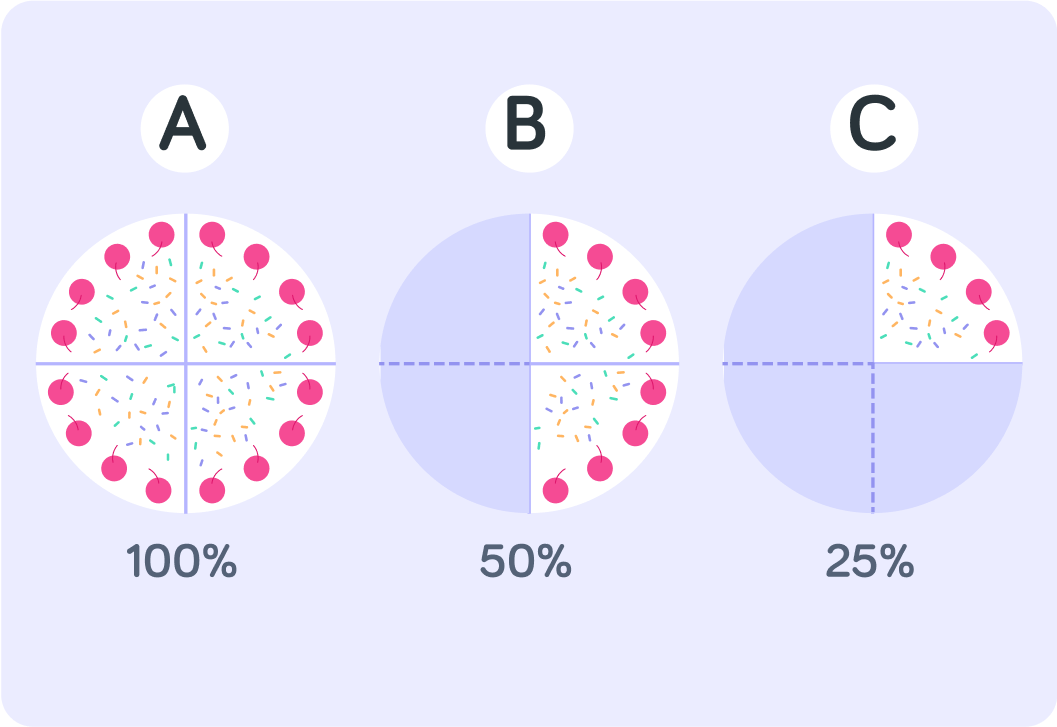
block image

5

So $100\%$ is the same as $\frac{100}{100}$ or $1$ whole

$50\%$ is the same as $\frac{50}{100}$ or $\frac{1}{2}$

$25\%$ is the same as $\frac{25}{100}$ or $\frac{1}{4}$

block image

1

How much is left of this pizza in $\%$ ?

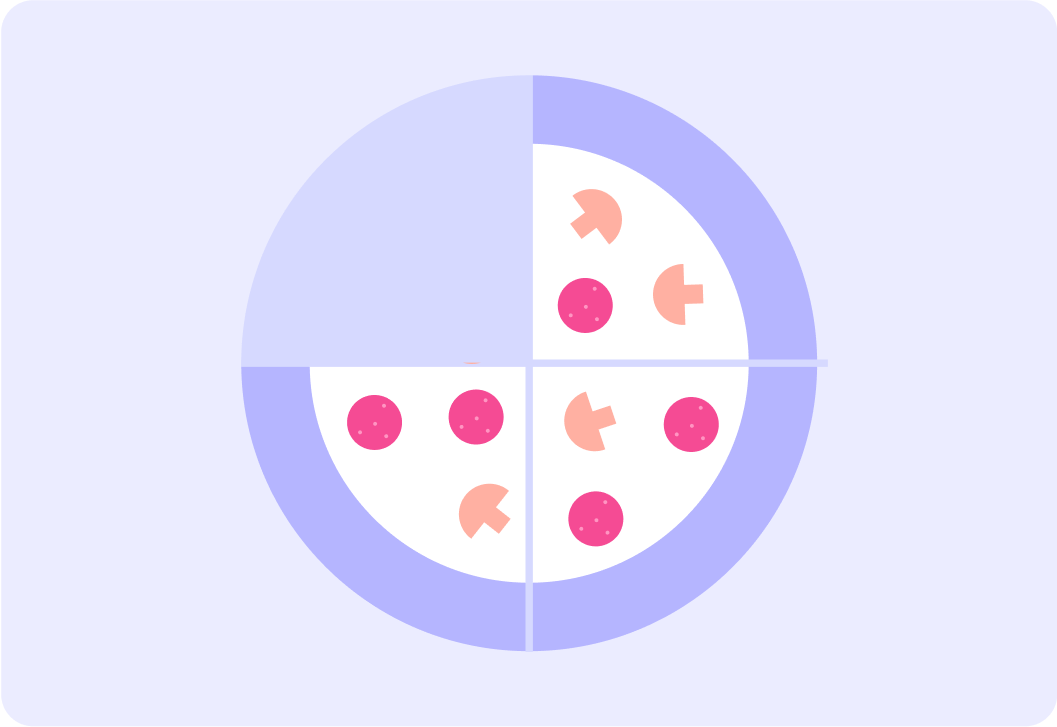
block image

How much is $\frac{69}{100}$ as a $\%$ ?

How do you write $24\%$ as a fully simplified fraction?

1

To recap! "Percent" means "per 100"

Here there are $\frac{37}{100}$ blocks filled in, so that is $37\%$

block image

2

$100\%$ is the same as $1$ whole

$\frac{75}{100}$ or $75\%$ is the same as $\frac{3}{4}$

$\frac{50}{100}$ or $50\%$ is the same as $\frac{1}{2}$

$\frac{25}{100}$ or $25\%$ is the same as $\frac{1}{4}$

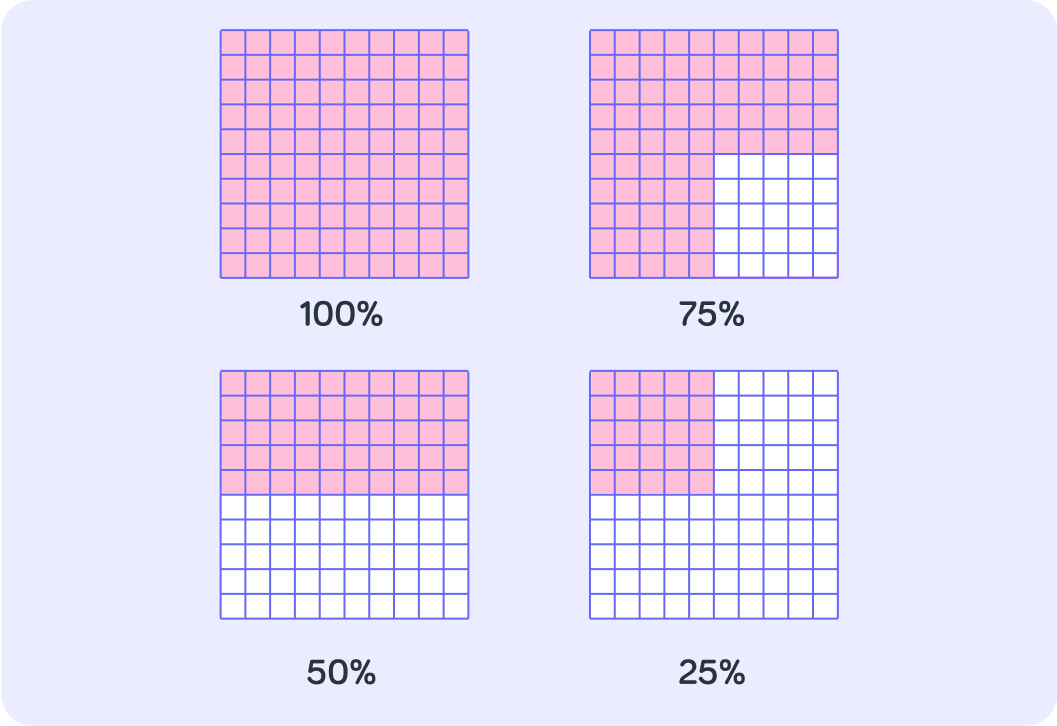
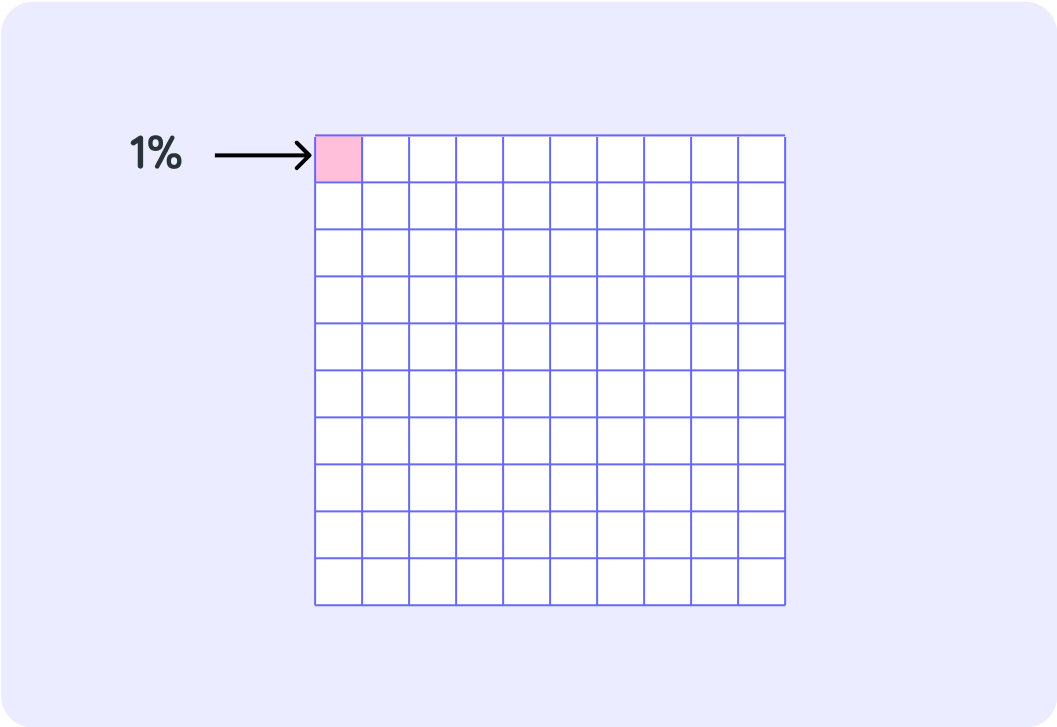
block image

1

So $1\%$ is the same as $\frac{1}{100}$

You can also say 1 hundredth.

block image

2

How many hundredths are in the decimal $0.43$ ?

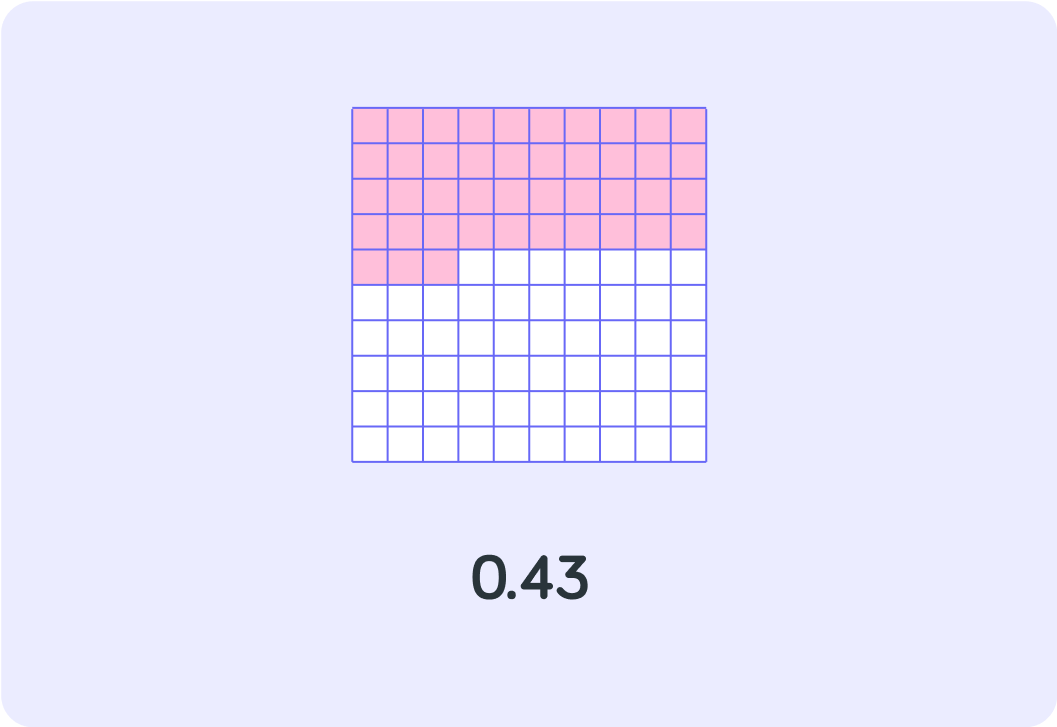
block image

3

How do you think you can write $0.43$ as a $\%$ ?

block image

4

So you can also change decimals to $\%$

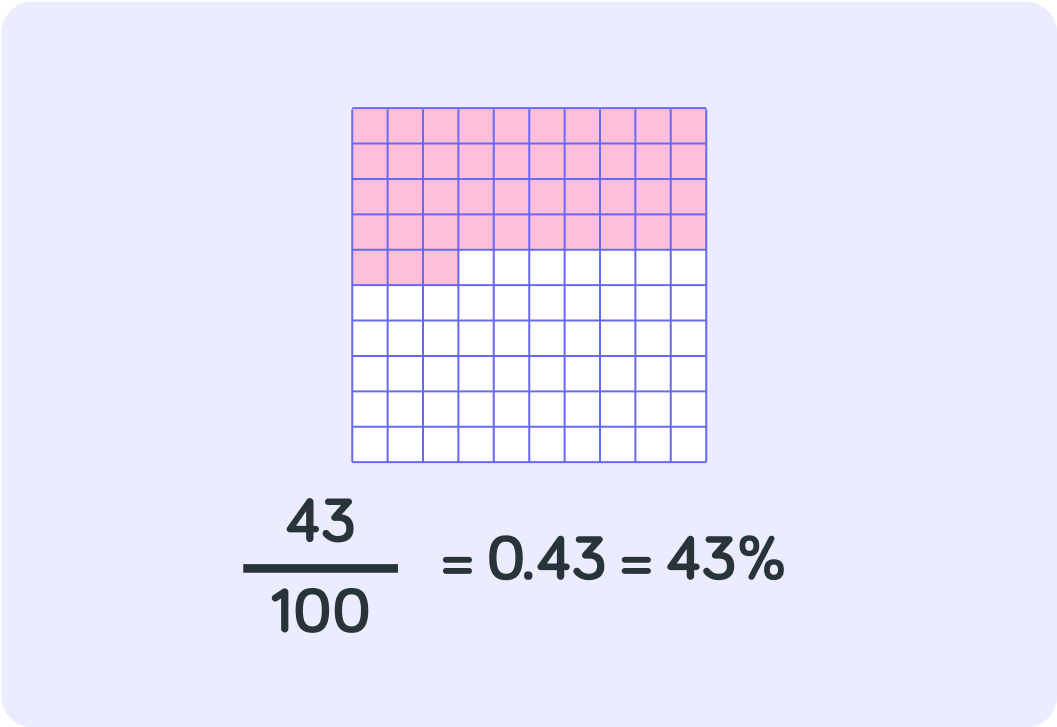
For example, $0.43$ is the same as $\frac{43}{100}$ which is the same as $43\%$

block image

How would you write $0.87$ as a $\%$ ?

Now, how much is $0.134$ in $\%$ ?

1

So what do you actually do when you change decimals into $\%$ ?

Have a good look at these examples again.

block image

2

You change decimals into $\%$ by _____________ by $100$

A) dividing B) multiplying

block image

3

You change decimals into $\%$ by multiplying by $100$

For example, $87\%$ is $\times100$ bigger than $0.87$

block image

Now, what is $8\%$ as a decimal?

Pick the 3 options below that are the same as $40\%$

You can select multiple answers

What is $200\%$ the same as?

Pick the 3 options below that are the same as $150\%$

You can select multiple answers

1

Summary! "Percent" means "per 100"

$100\%$ is the same as $1$ whole.

block image

2

You can change between fractions, decimals and percent

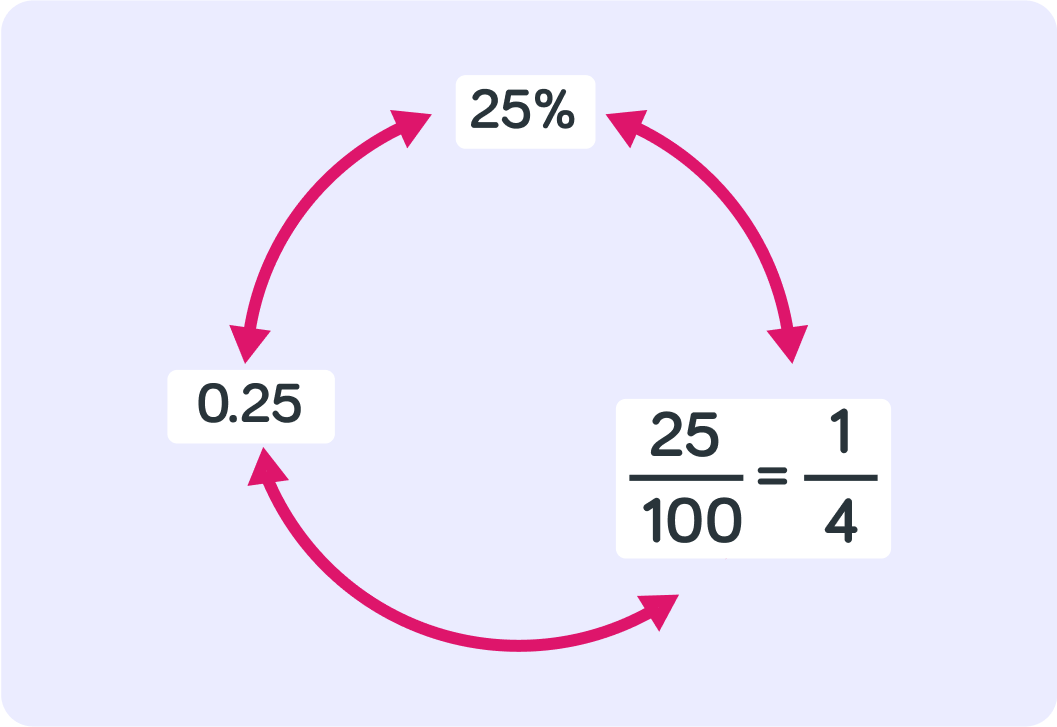
For example, $25\%$ is the same as $\frac{25}{100}$ or $\frac{1}{4}$ which is also the same as $0.25$

block image