Basic Concepts in Physics

YOU ARE LEARNING:

Acceleration as a Vector

The "direction" of acceleration is whether acceleration is positive or negative.

Acceleration is a vector ** quantity*, which means it has both a magnitude and a direction.*

Acceleration is a vector quantity, so it has both a magnitude and a direction

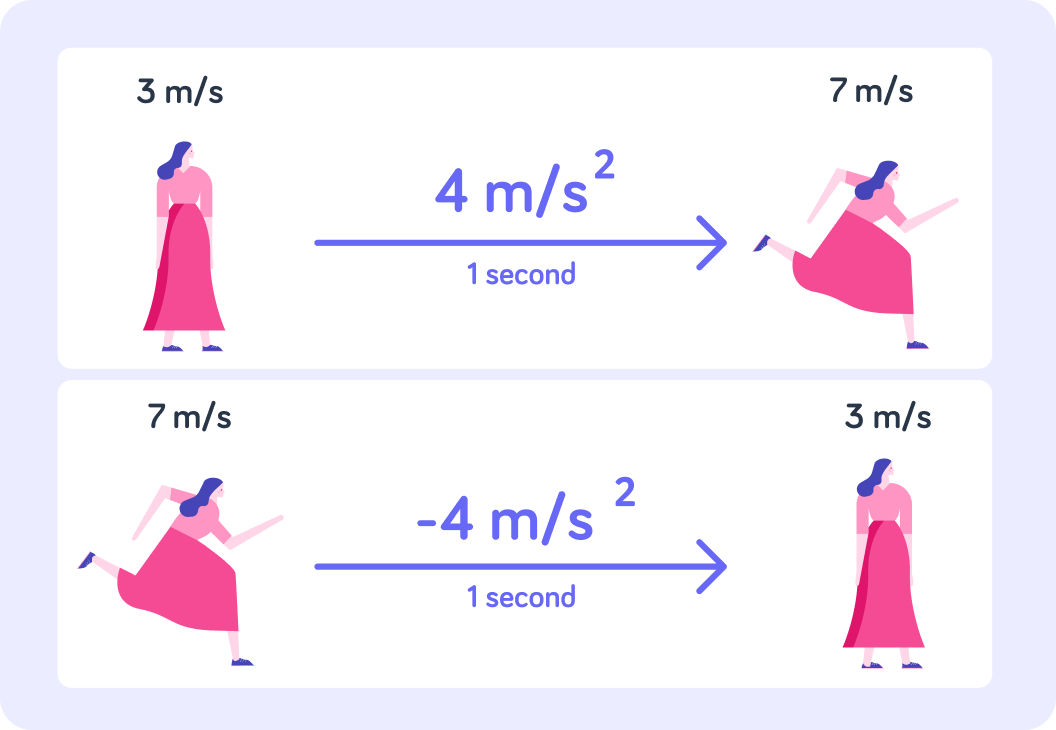
This woman is going from a speed of $3 \space m/s$ to a speed of $7 \space m/s$ . Is she speeding up or slowing down?

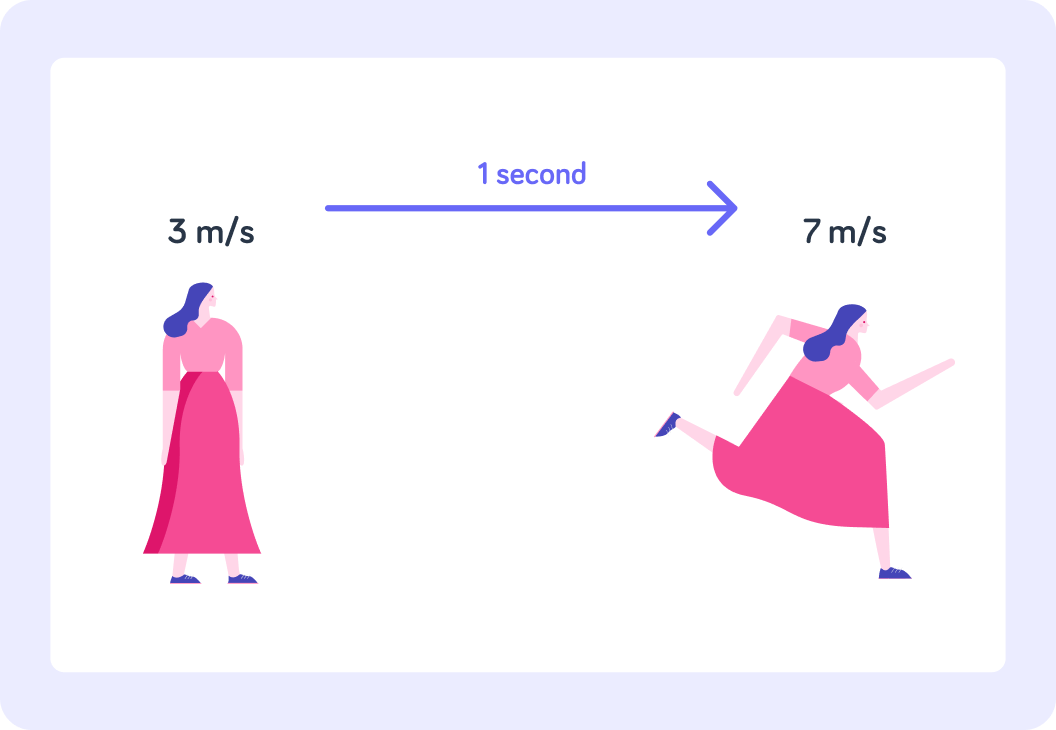
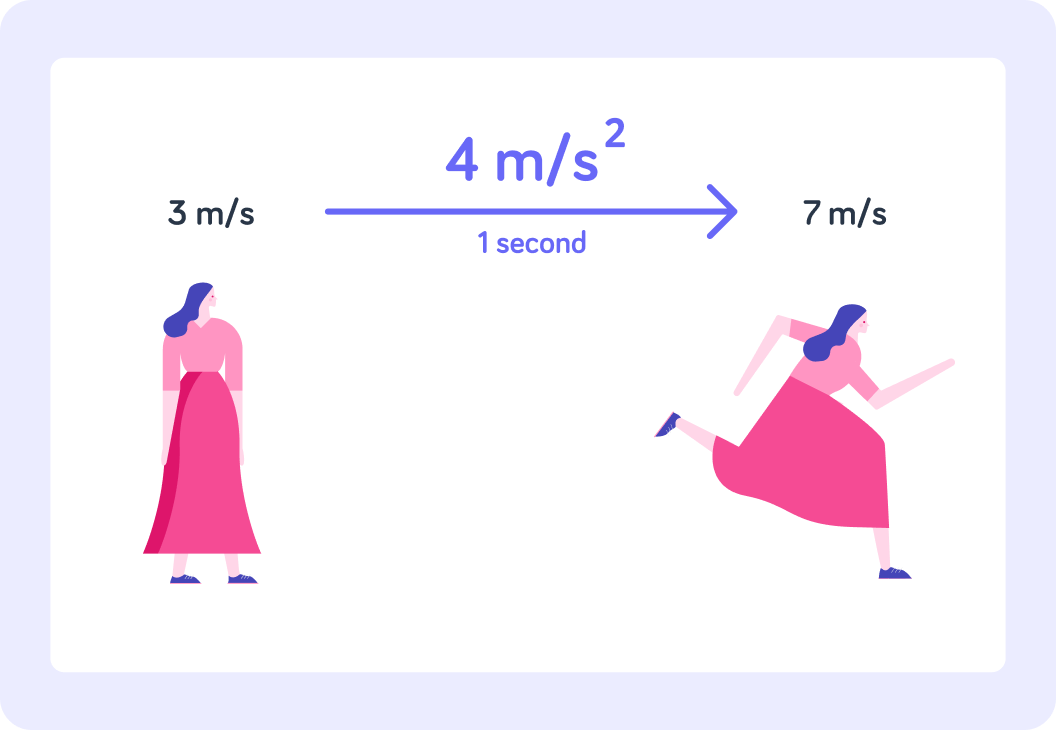
The woman is speeding up from $3 \space m/s$ to $7 \space m/s$

She does that over the course of just one second, so her acceleration is $4 \space m/s^2$

Now the woman is going from a speed of $7 \space m/s$ to $3 \space m/s$ . Is she speeding up or slowing down?

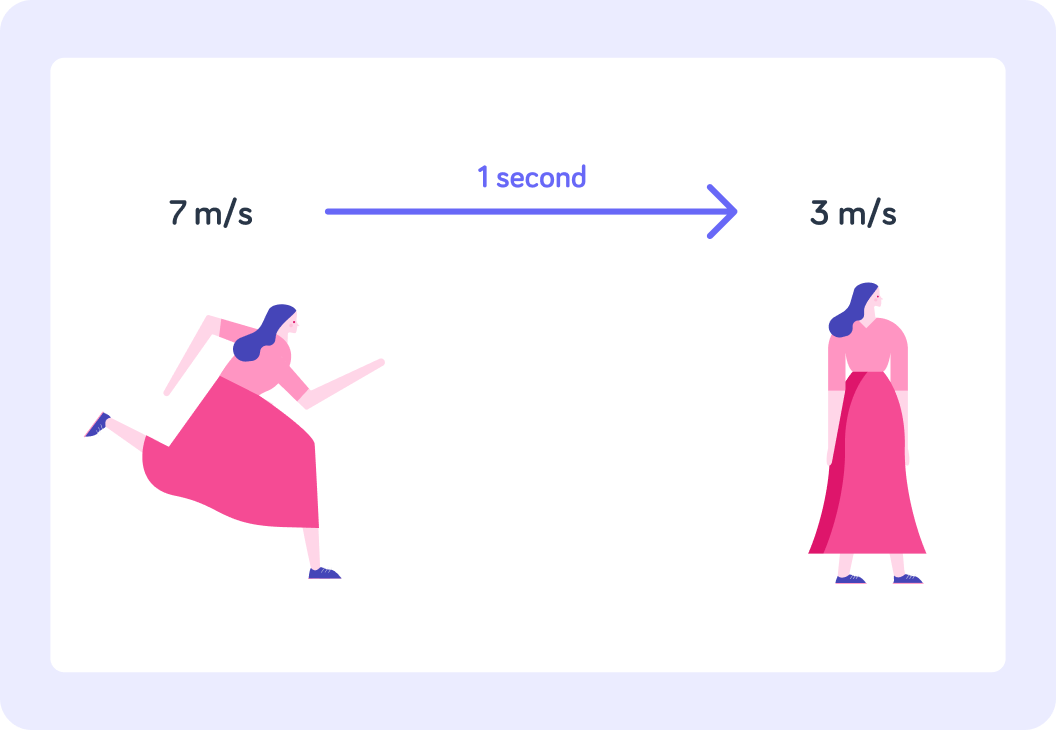
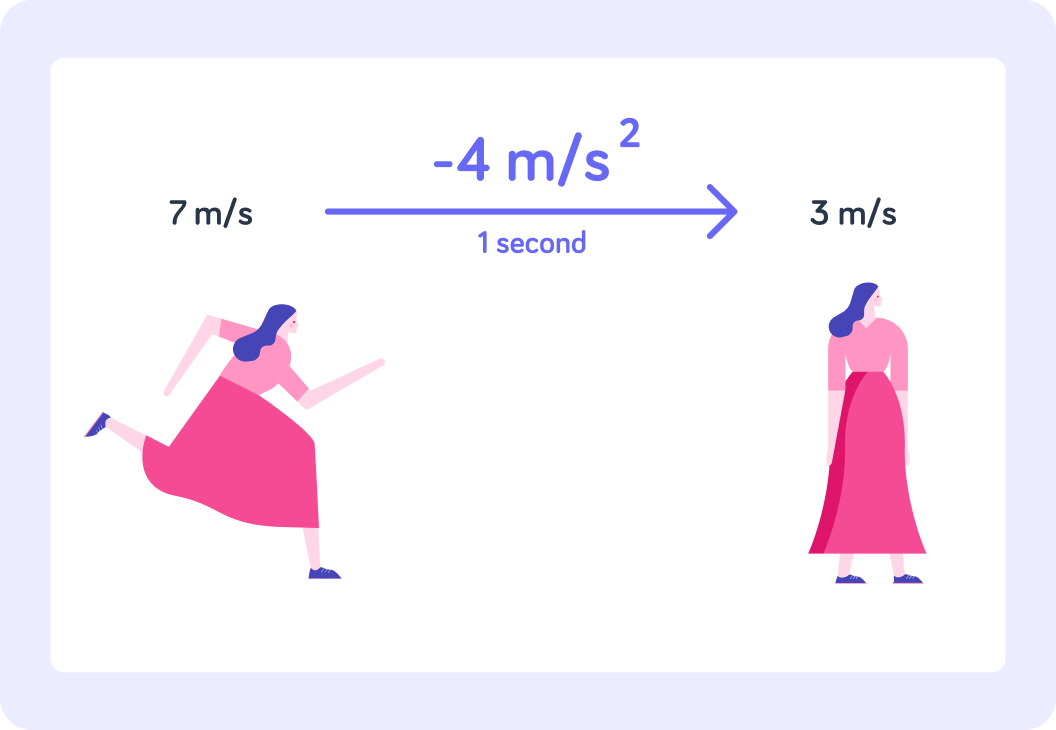
The woman is now slowing down again from $7 \space m/s$ to $3 \space m/s$

She does that over the course of just one second, so her acceleration is now $-4 \space m/s^2$

Acceleration's "direction"

What do you think we mean by the "direction" of acceleration?

When an object is speeding up, acceleration is _______________.

When an object is slowing down, acceleration is _______________.

Summary!

So the "direction" of acceleration refers to whether acceleration is positive or negative

If positive, like $4 \space m/s^2$ , the object is speeding up. If negative, like $-4 \space m/s^2$ , the object is slowing down.