Forces in Motion

YOU ARE LEARNING:

Calculating Newton's Second Law

We can use the equation derived from Newton's Second Law to find the resultant force, acceleration and mass of an object.

True or false? With the same resultant force, an object with less mass will accelerate less than an object with more mass.

Newton's second law can be written as a formula describing the relationship between force, mass and acceleration. If an object with a mass of $25\space kg$ accelerates at a rate of $3\space m/s^{2}$ with a resultant force of $75\space N$ , what is the formula?

If a car with a mass of $1600\space kg$ accelerates at $4\space m/s^{2}$ , how much force is the engine producing?

A tennis ball has a mass of $0.2\space kg$ . It accelerates at a rate of $112\space m/s^{2}$ when hit by the tennis racket. How much force does the tennis players racket exert on the ball?

Newton's second law can be written as $Force = mass\times acceleration$ , or $F = ma$ . To find the force, we simply multiply mass and acceleration. The formula can also be rearranged to find mass, or acceleration.

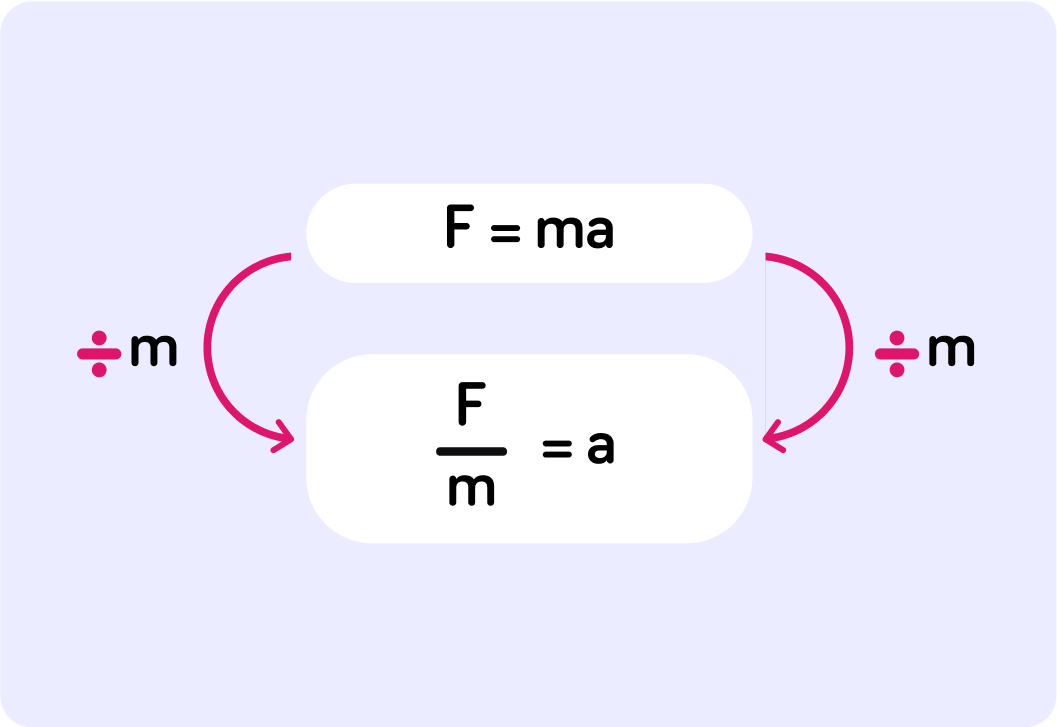
To rearrange the formula to make acceleration the subject, divide both sides of the formula by mass.

$acceleration =\frac{Force}{mass}$

Another way to rearrange a formula is to put it into a triangle. You simply cover the variable you are looking for, and you are left with the correct formula!

If we cover up acceleration, the triangle tells us that the formula to find it is $\frac{Force}{mass}$

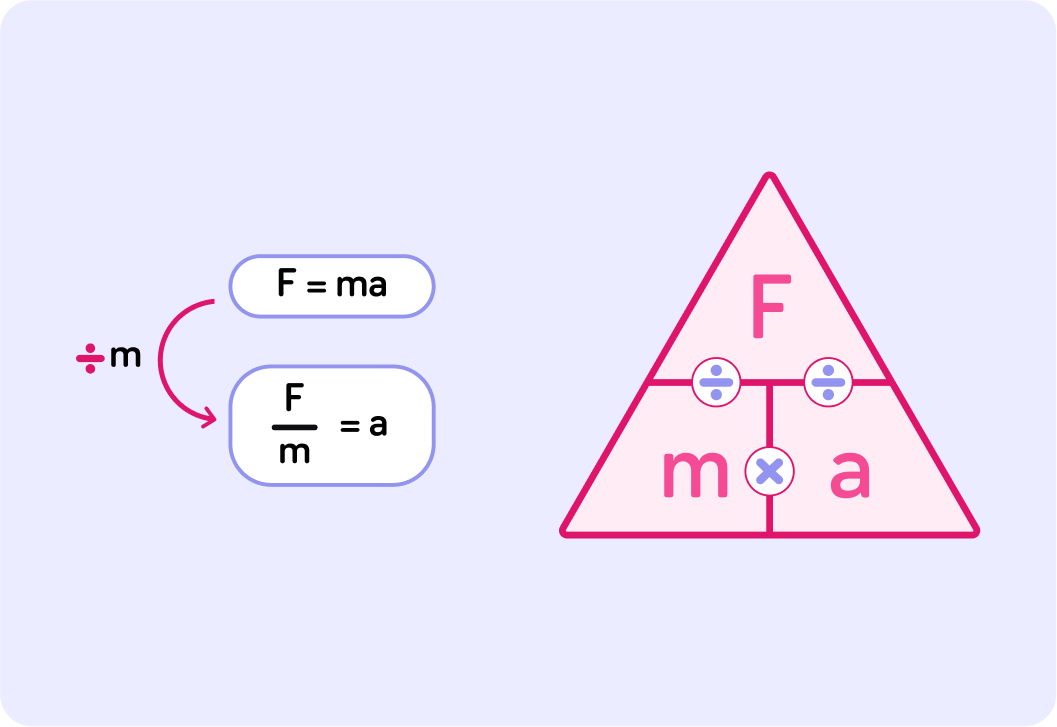
Using either of these methods, find the formula to calculate mass if you are given the force and acceleration.

A) $mass = Force \times acceleration$ B) $mass=\frac{acceleration}{Force}$ C) $mass=\frac{Force}{acceleration}$

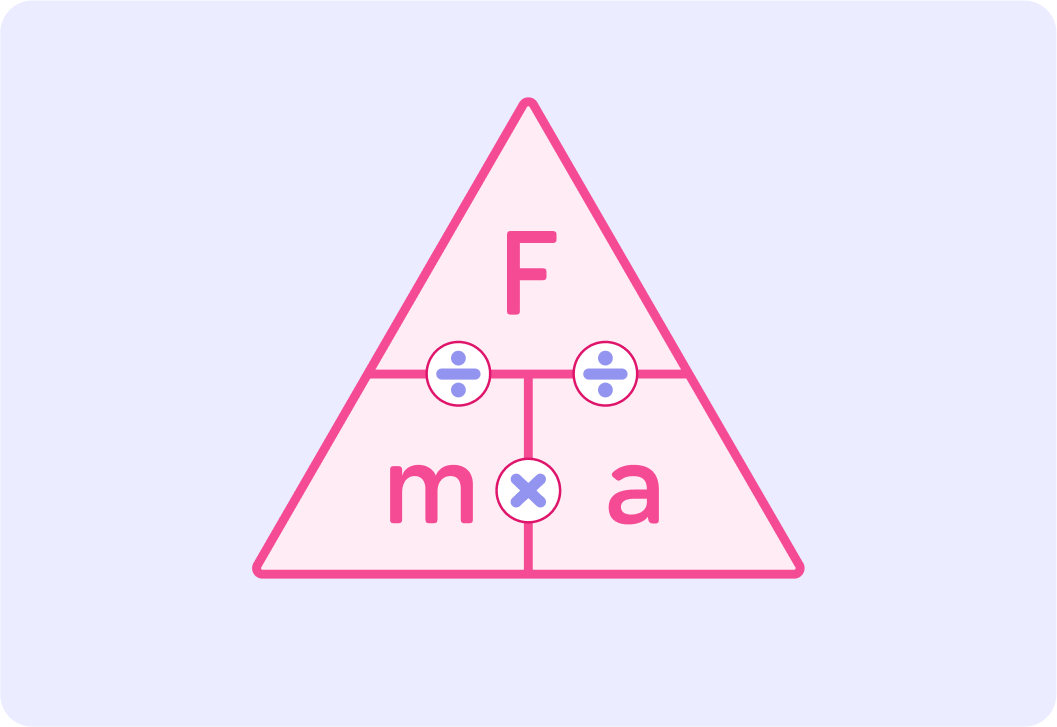
If you push a trolley with $15\space N$ of force, and it accelerates at $0.5\space m/s^{2}$ , what is the mass of the trolley?

If a $62\space kg$ runner exerts a force of $45\space N$ , what is his acceleration?

Sometimes, we need to find the resultant force acting on an object before being able to apply the formula. Remember that if two forces are acting in the same direction, you add them together to find the resultant. If they are acting in opposite direction, you subtract them.

A motorcycle is accelerating. It has a forwards driving force of $1800\space N$ , and the magnitude of the drag force acting in the opposite direction is $650\space N$ . The mass of the motorcycle and the driver is $210\space kg$ . What is the acceleration?

What is the resultant force acting on the motorcycle?

The acceleration of the motorcycle is ...

A) $8.6\space m/s^{2}$ B) $1.8\space m/s^{2}$ C) $5.5\space m/s^{2}$ .

You push a box with a force of $12\space N$ . The opposing force of friction has a magnitude of $5\space N$ and the box accelerates at a rate of $0.2\space m/s^{2}$ . What is the mass of the box?