Albert Teen
powered by
Albert logo
GCSE Exam GuideParent
GCSE Exam
>
Physics
>
Forces in motion
>
Inertial mass
Forces in Motion

YOU ARE LEARNING:

Inertial Mass

Inertial Mass

Inertial Mass

Sometimes it is more difficult to change the velocity of an object than others. Inertial mass is a measure of inertia.

A book resting on a desk will remain at rest. What is needed to change the state of motion of the book?

A cyclist is riding in a constant direction and at a steady speed. What is needed to change the velocity of the cyclist?

What do all objects have a tendency to do?

All objects with mass have inertia. What is inertia?

All objects have a natural tendency to carry on in the same state of motion. This is why objects at rest will remain at rest, and objects in motion will remain in motion in the absence of an unbalanced force. We call this resistance to a change of motion inertia.

If a car has more inertial mass than a bike, and an elephant has more inertial mass than a mouse, then what is inertial mass?

All objects have inertia, meaning they will resist any changes to state of motion unless acted on by an unbalanced force. Inertial mass is a measure of how difficult it is to change its state of motion.

For example a car has greater inertial mass than a bike. Therefore, a resultant force with a larger magnitude is needed to change the car's state of motion compared to the bike.

Which has less inertial mass?

1

Which do you think has more inertial mass? Answer either car or van.

2

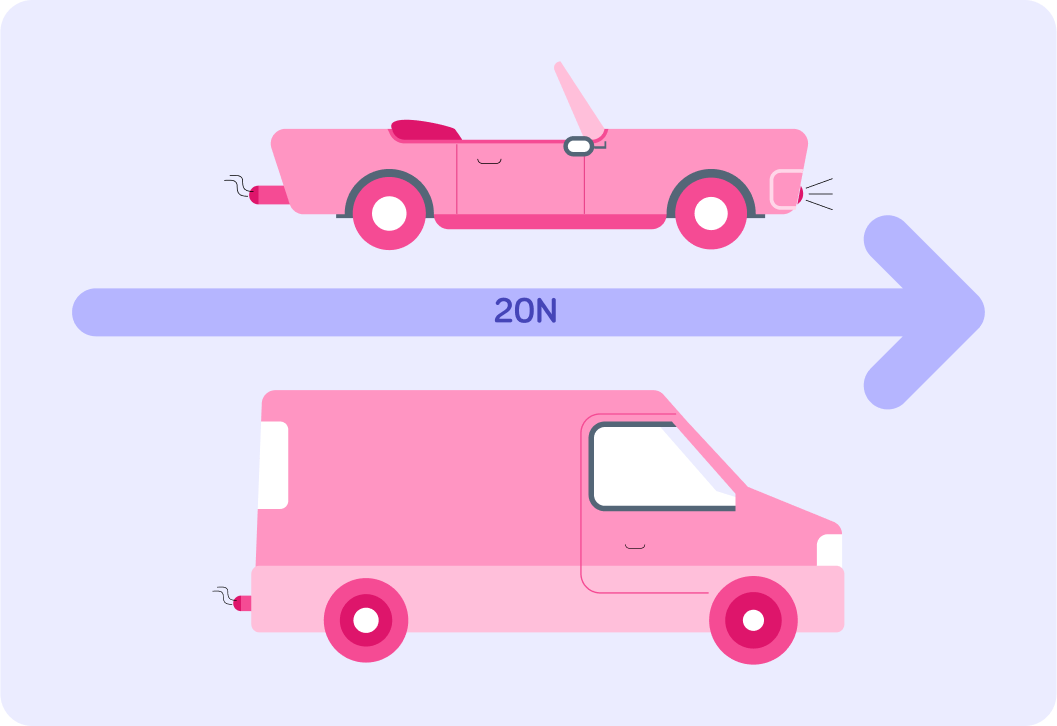
A resultant force of 20 N20\space N acts on both vehicles causing an acceleration. Which vehicle will accelerate more? Answer either car or van.

If we know the force causing a change of velocity, we can calculate the inertial mass of an object. If a force of 7.5 N7.5\space N accelerates an object with an inertial mass of 5 kg5\space kg at a rate of 1.5 m/s21.5\space m/s^{2} , what is the formula that links inertial mass, force and acceleration?

To find an object's inertial mass, we can use the formula Inertial mass=forceaccelerationInertial\space mass = {force\over acceleration} which you also write as m=fam={f\over a} . This is a rearrangement of the formula describing Newton's second law of motion.

If you hit a golf ball with a force of 1 N1\space N , and it accelerates at a rate of 20 m/s220\space m/s^{2} , what is the inertial mass of the golf ball?

If you throw a bowling ball with a force of 9 N9\space N , and it accelerates at a rate of 1.8 m/s21.8\space m/s^{2}, what is the inertial mass of the bowling ball?