YOU ARE LEARNING:
Conservation of Momentum
Conservation of Momentum
Conservation of Momentum describes a law in a closed system for before and after an event. We will use this concept to do calculations of colliding objects.
If the red ball is stationary and the white ball is moving, which is true?
A) They both have momentum B) Only the red ball has momentum C) Only the white ball has momentum
Answer A, B or C.
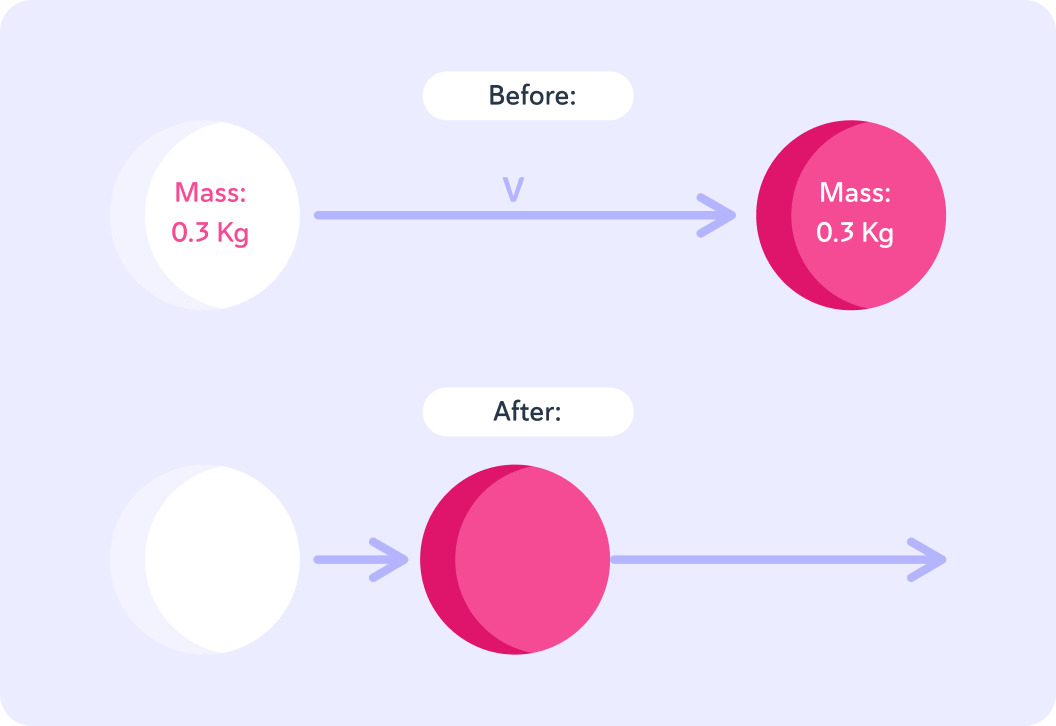
The white ball collides with the red ball causing it to move, so now both balls have momentum. Look at the velocity vector. The momentum of the white ball has...
A) decreased B) increased C) stayed the same
Answer A, B or C.
This is an example of conservation of momentum.
After the collision, the white ball's momentum has decreased, but the red ball has gained momentum. The overall momentum of both, is equal to that of the white ball before the collision.
In a closed system, the total momentum before an event is the same as after the event. This is called conservation of momentum. An event can refer to a collision or an explosion.
If two cars collide, the total momentum of the two cars after the event is...
If two objects collide and one object loses momentum, the other must...
You can think about momentum as if was "shared" between the two objects in a collision. The amount object 1 loses is the same amount object 2 gains.
Each ball has a mass of . The white ball is moving with a velocity of. How much momentum does it have? Give your answer in .
When the balls collide, momentum is conserved. The white ball now has momentum of , what is the momentum of the red ball?
Lorry A is stationary, so it has no momentum. What is the momentum of lorry B?
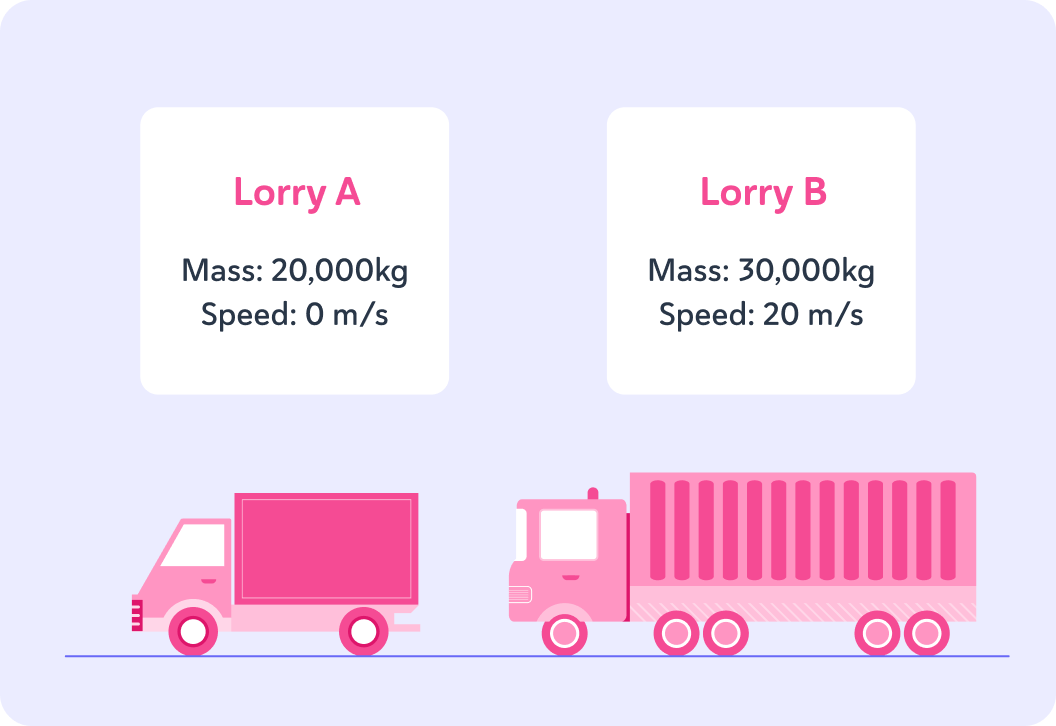
If lorry B collides with lorry A and its speed reduces to , what is its momentum after the collision?
What is the momentum of lorry A after the event?
Is momentum conserved when there is a change of mass?
A moving car hits a parked car and they stick together. The vehicles (now stuck together) continue to move in the same direction as the moving car was moving, but at a lower velocity.
We can use conservation of momentum to explain this.
If the mass of the moving car is and its velocity is , what is its momentum?
We know that the momentum after collision must be the same as before collision.
The total momentum after the collision must be of .
Now that the cars are stuck together, their combined mass is . If you know that the cars have momentum of , what speed do they move at after the collision?
The increase in mass causes a decrease in velocity.
This demonstrates that momentum is conserved when there is an increase in mass.
A white snooker ball moving at strikes a red ball and pots it. Both balls have the same mass of . If the white ball continued in the same direction at , what was the velocity of the red ball after the collision?
How is momentum conserved in explosions?
Think about a bullet being fired from a rifle. The momentum before the explosion is zero as both the bullet and the rifle are at rest, so what must the momentum be after the explosion?
If the bullet gains of forwards momentum, how must the momentum of the rifle change for the sum of both the bullet and rifle's momentum to be zero?
Total momentum is conserved
Because the momentum is in different directions, the vector sum of the individual momentum of the bullet and the rifle is zero.
A bullet of mass is fired from a rifle of mass which recoils with a velocity of . What is the velocity of the bullet?
What is the momentum of the rifle after the explosion?
If the momentum of the rifle is , then the bullet must have the same magnitude of momentum in the opposite direction.
This is conservation of momentum.
If the momentum of the bullet is , and its mass is , you can rearrange to find its velocity. What is the velocity of the bullet?