Forces in Motion

YOU ARE LEARNING:

Forces and Extension-Load

You can perform an experiment where you measure how much an elastic object stretches with an object due to an acting force. An Extension-Load graph shows this.

If a stretched spring measured $1 0\space{cm}$ before a force is applied, and $18\space{cm}$ afterwards, what is the extension of the spring?

The extension of an object is how much an elastic object has stretched because of an applied force. An easy way to find the extension is to subtract the original length, from the new length.

A spring is measured at $25\space{cm}$ after a force of $8\space{N}$ is applied to it. The extension is $19\space{cm}$ . What was the original length of the spring?

The image above shows apparatus that we can use to investigate force and extension.

Notice that there is more than one force acting on the spring!

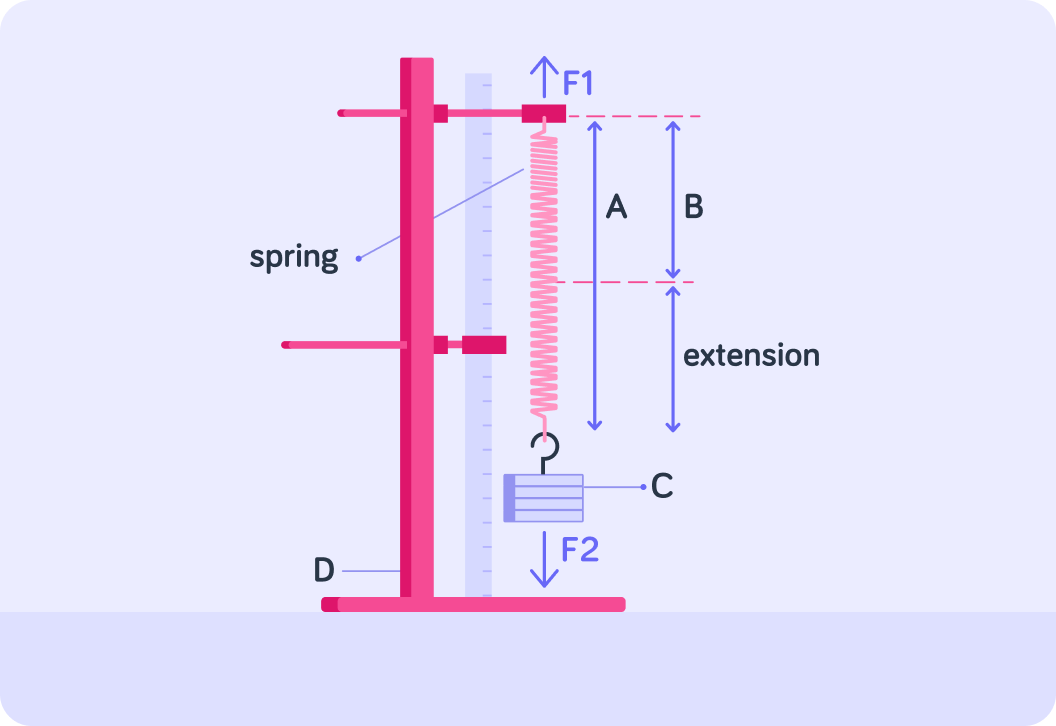
Which force has the largest magnitude? Answer force 1 or force 2.

A clamp stand is used to keep the apparatus in place. Is the clamp stand labelled A,B,C, or D?

Once the apparatus is in place, you would measure the initial length of the spring. Is this length shown in the diagram as A,B,C, or D?

Next, you would hang a known mass from the spring (C) and measure the new spring length (A).

You could repeat these steps with different masses to investigate the relationship between load and extension.

You might have noticed that an extension-load graph does not show the force applied to the spring. We can calculate the force from the mass, and gravitational field strength. On Earth, gravitational field strength is always $9.8\space{N/kg}$ , but you can round up to 10.

A spring is pulled downwards with a force of 10 Newtons when a mass of 1 kg is hung from it. Now, try to figure out which one is the correct formula that links mass, gravitational field strength and force. Click the hint button if you need it.

We can calculate the force $(w)$ acting on an object from a known mass using the formula $w=mg$ , where $m$ is mass in kilograms, and $g$ is gravitational field strength (in newtons per kilogram). If you are given the mass in grams, you can convert to kilograms by dividing by 1000.

If gravitational field strength on Earth is $10\space{N/kg}$ , how much force is applied to the spring from a $200\space{g}$ mass?

If gravitational field strength on Earth is $10\space{N/kg}$ , how much force is applied to the spring from an $800\space g$ mass?

If you were to continue applying more force to a spring, you would notice that eventually it would no longer return to its original shape and length when the force is removed. We call this inelastic deformation. This happens above the limit of proportionality.

If directly proportional means that as the force is increased, the extension increases at the same rate, then try to guess what happens after the limit of proportionality? Pick all the statements below that you think are correct.

You can select multiple answers