Algebra

YOU ARE LEARNING:

Expanding Brackets

Expanding brackets is an important step for manipulating expressions, and involves multiplying the terms inside a bracket by those outside of a bracket.

What does this equal?

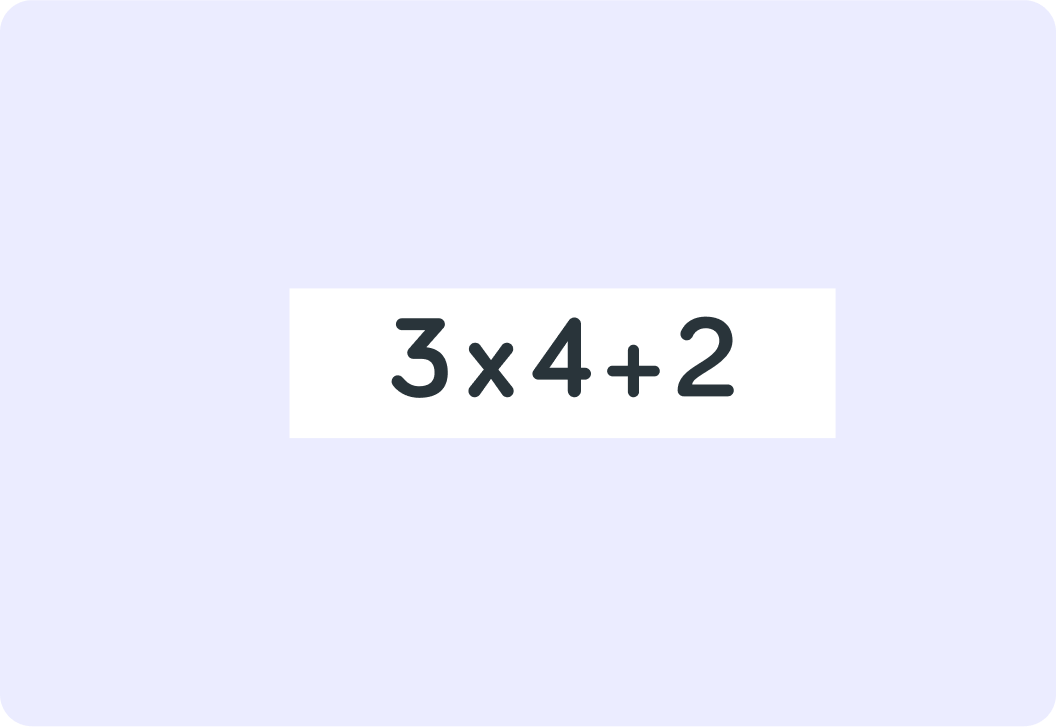
What if we add brackets? What does this equal now?

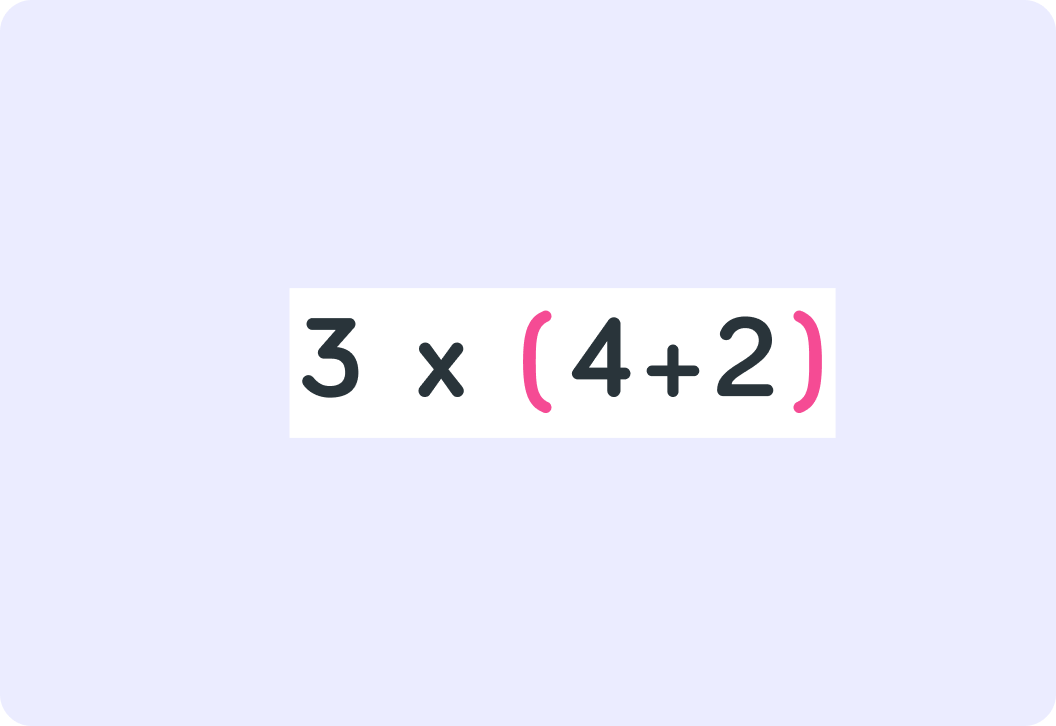
So brackets matter for the result!

By the way, notice that when you multiply brackets, you don't need to write the multiplication sign.

$3 \times (4+2)$ is the same as just $3(4+2)$

Now, you could also work out this problem in a different way

You could also change the expression so that the brackets disappear. That is called expanding the brackets.

Basically, the $3$ wants to be multiplied by both terms inside the brackets. What is $3 \times 4$ ?

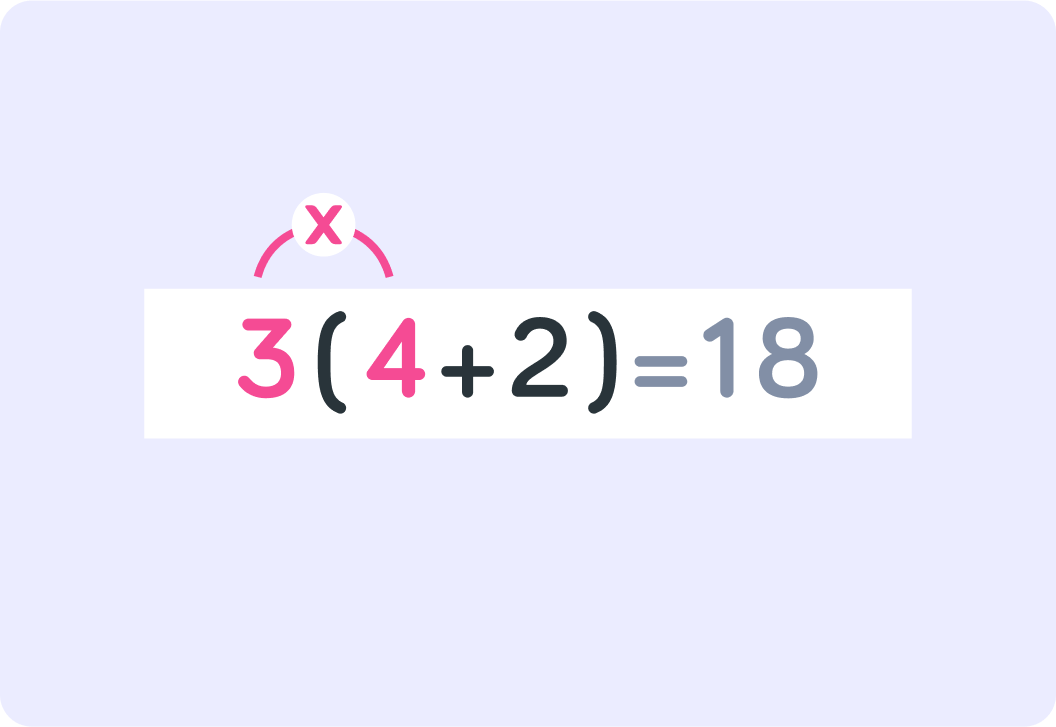
And what is $3\times2$ ?

Now, you have $12+6$

So $12+6$ is the same as $3(4+2)$ , but you have expanded the brackets - you have made them disappear.

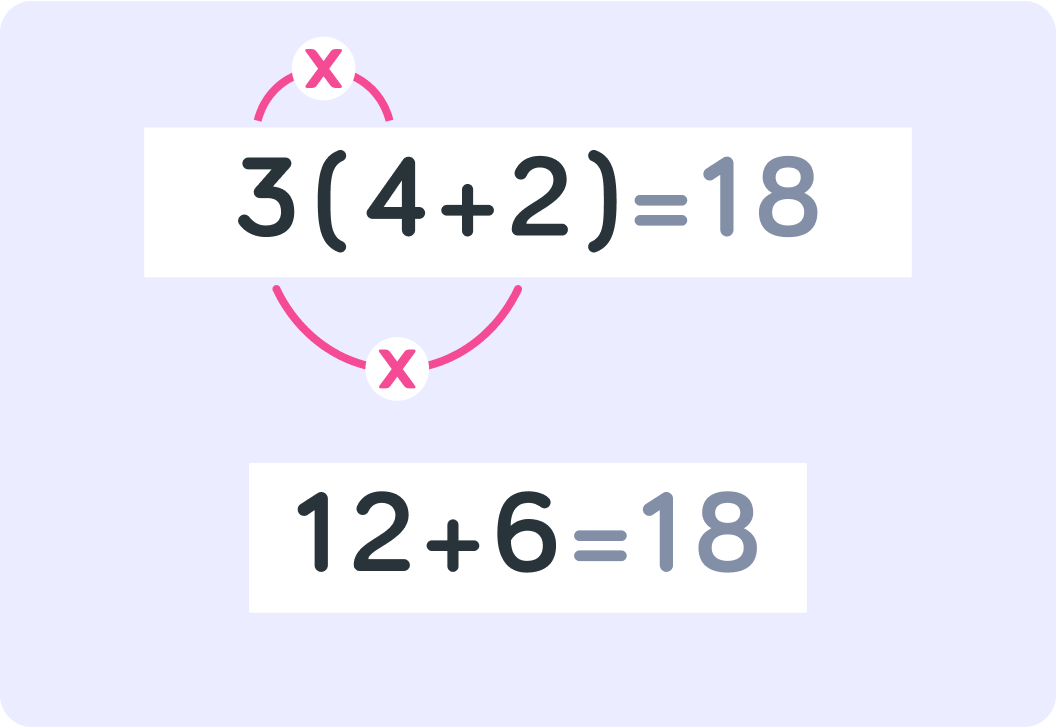
But why would you want to expand brackets?

It can help you simplify expressions to make them easier to read. This example shows you how.

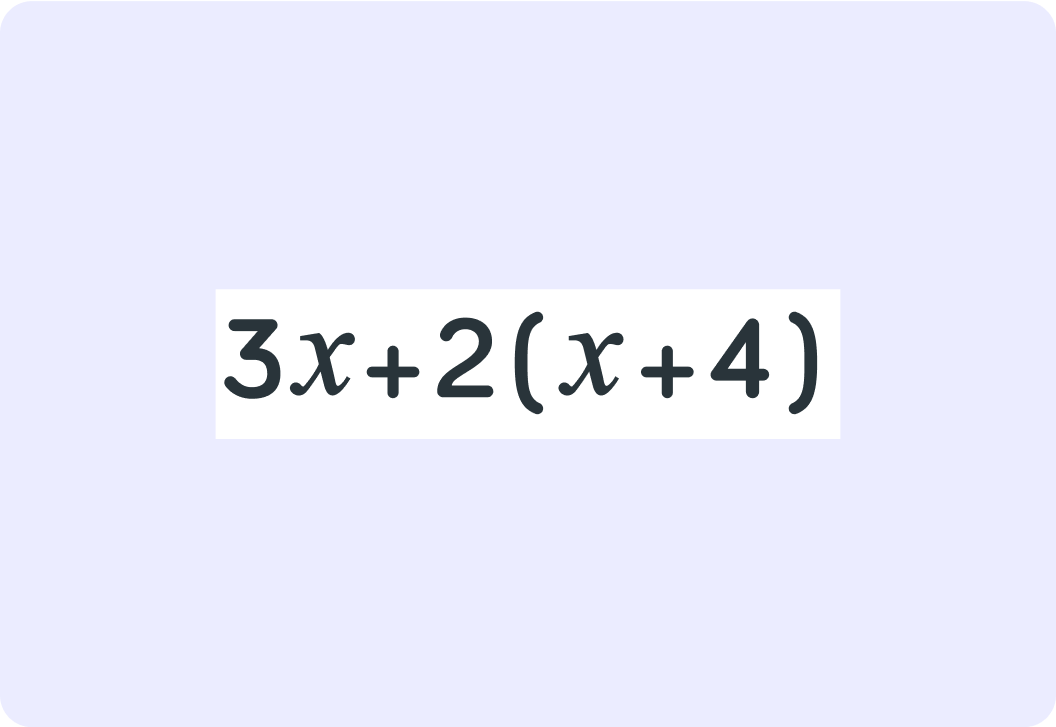
To expand the brackets here, you first have to say $2 \times x$ . What is that?

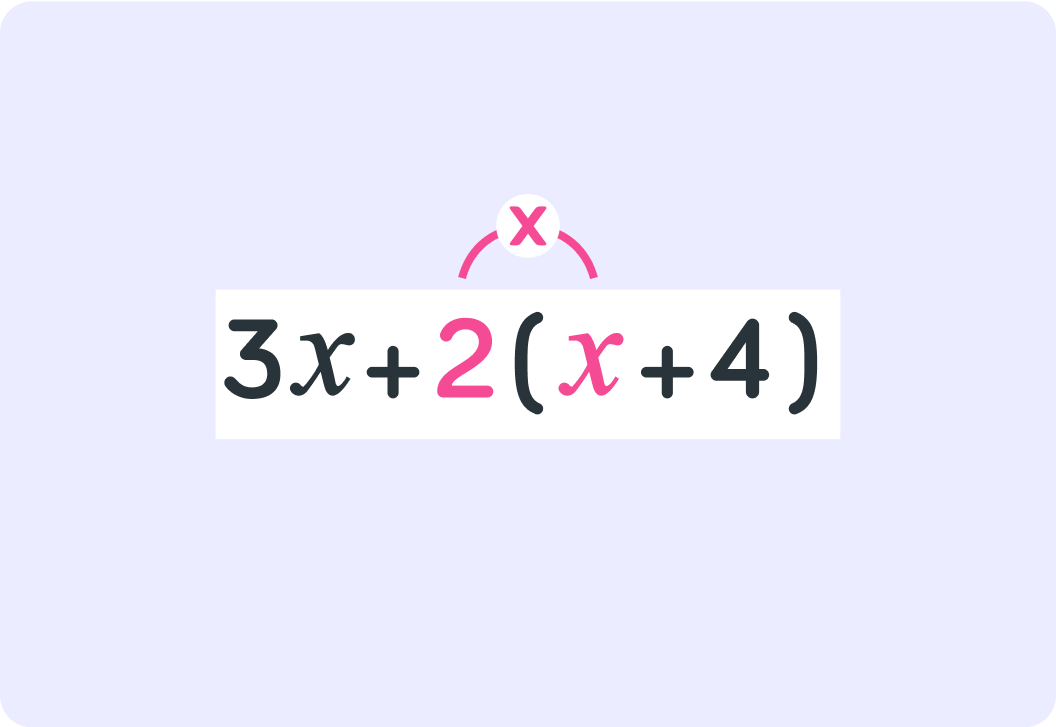
Then you say $2\times 4$ . What is that?

Now the brackets are expanded

Now you can simplify the expression.

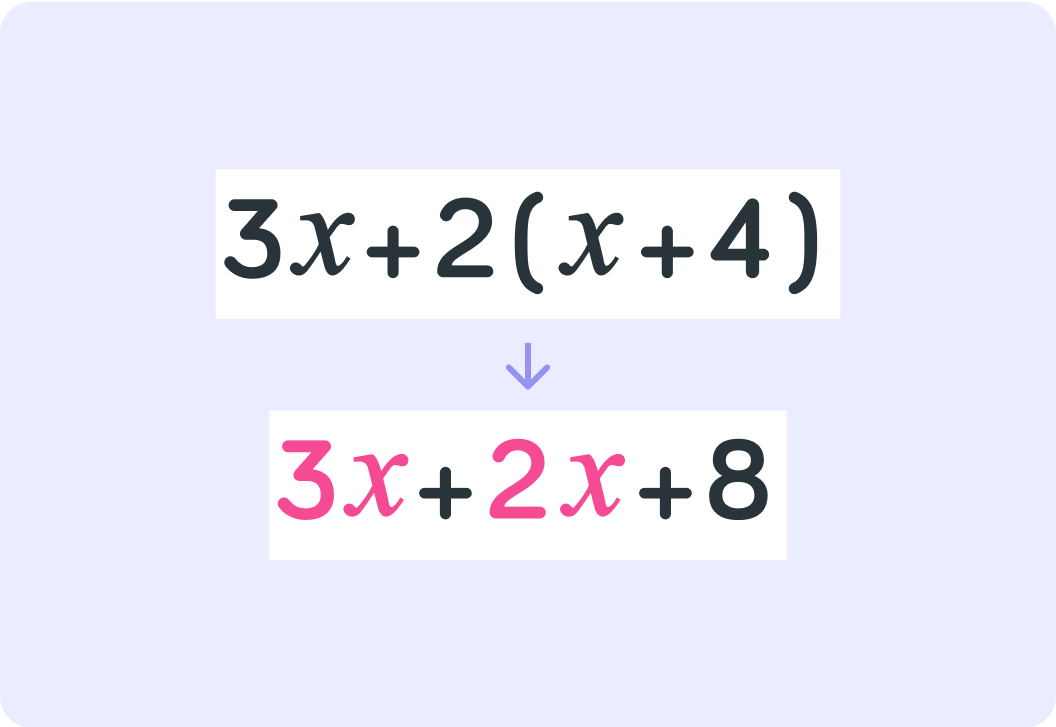
You have $3x$ and another $2x$ . How many $x$ is that in total?

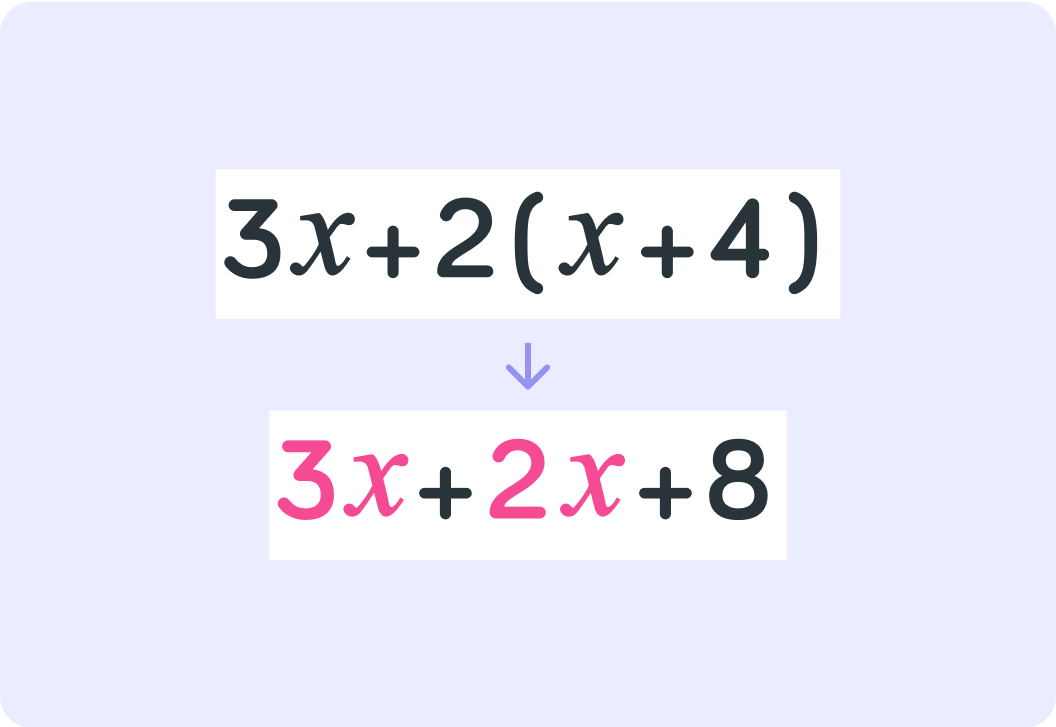
So you expanded the brackets to simplify this expression

$5x+8$ is a lot easier to read than $3x+2(x+4)$

Expand $5(3+x)$

Recap! You can expand brackets to simplify expressions

For example, $6x+20$ is a lot easier to read than $2x+4(x+5)$

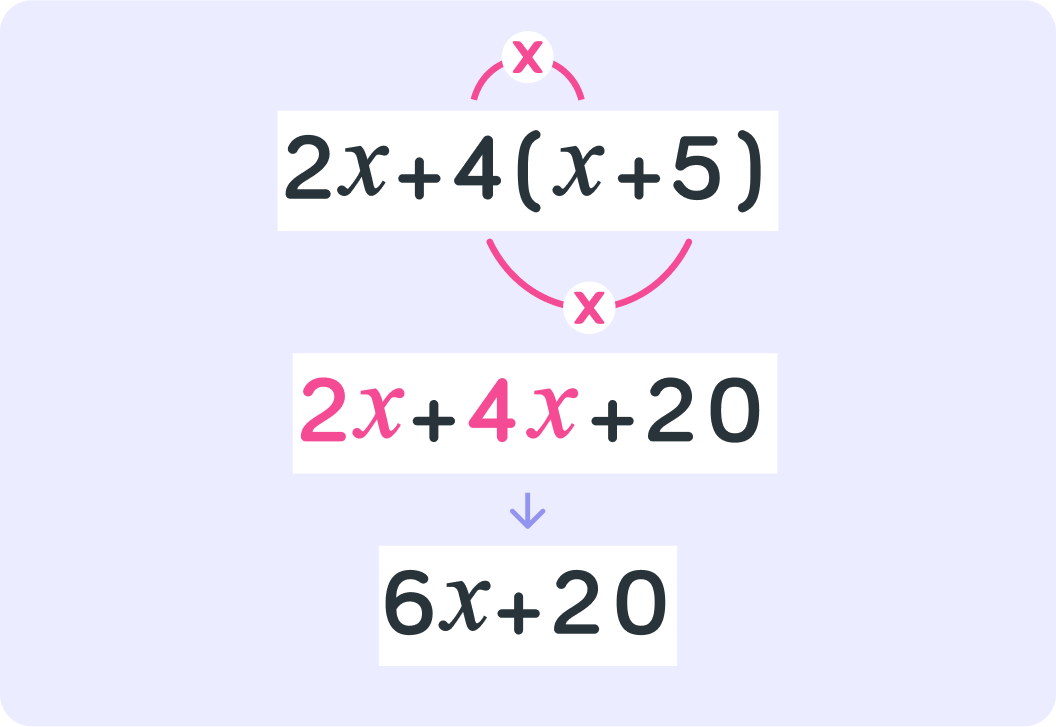
To expand brackets, you need to multiply all the terms inside the brackets by the number outside the brackets

First you say $4 \times x=4x$ Then you say $4\times5=20$ Then you put the two together $4x+20$

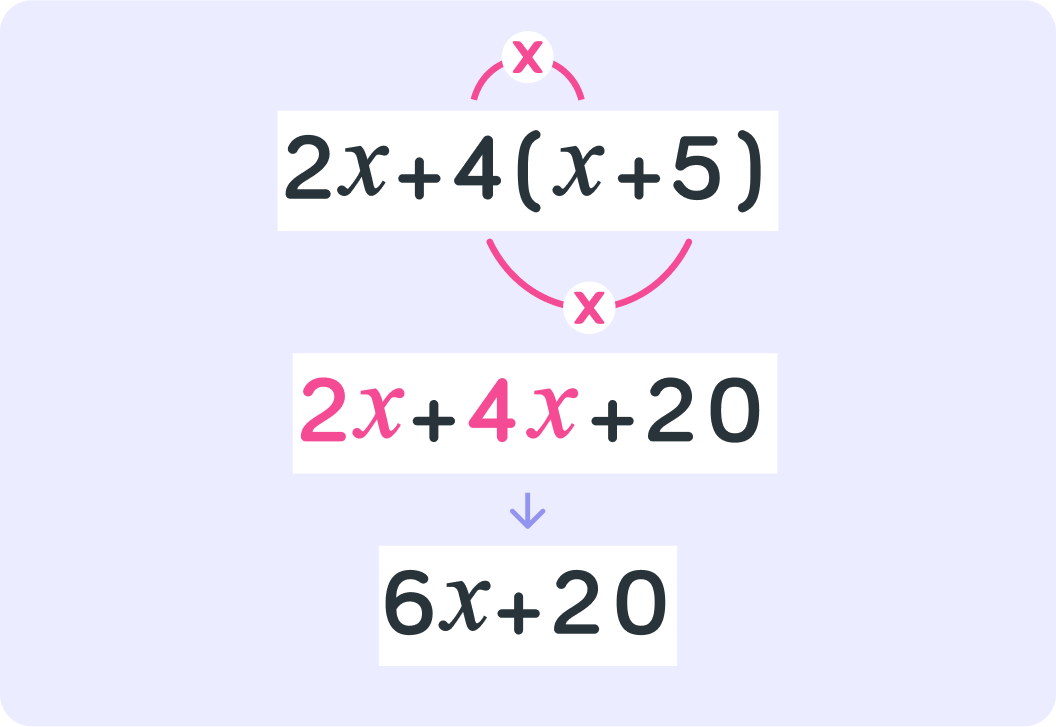
Finally, you can see if you can simplify the whole expression

In this case, you have $2x$ and $4x$ which you can combine to $6x$

Expand $6(x+2)$

Expand $(x+6)8$

Now, what is $2(x-4)$ when you expand the brackets?

Let's try this one $x(3x+6)$ .

What happens when the number outside the bracket is also a variable?

We apply the same principle.

First we multiply $x\times 3x$ . What does this give us?

Next we multiply the second term in the bracket. What is $x\times 6$ ?

We have $x\times 3x=3x^2$ and $x\times 6=6x$ .

Putting these together we have $3x^2+6x$ .

Expand $(x-2)4x$

Expand and simplify $(2+3x)5-4x$

Expand and simplify $x(8+3x)-2x$

Summary! You can expand brackets to simplify expressions

For example, $6x+3x^2$ is easier to read than $x(8+3x)-2x$

So how do you expand brackets?

You multiply both terms inside the bracket by the number outside the bracket.

The number might follow the brackets rather than stand before them

Don't be confused by that.

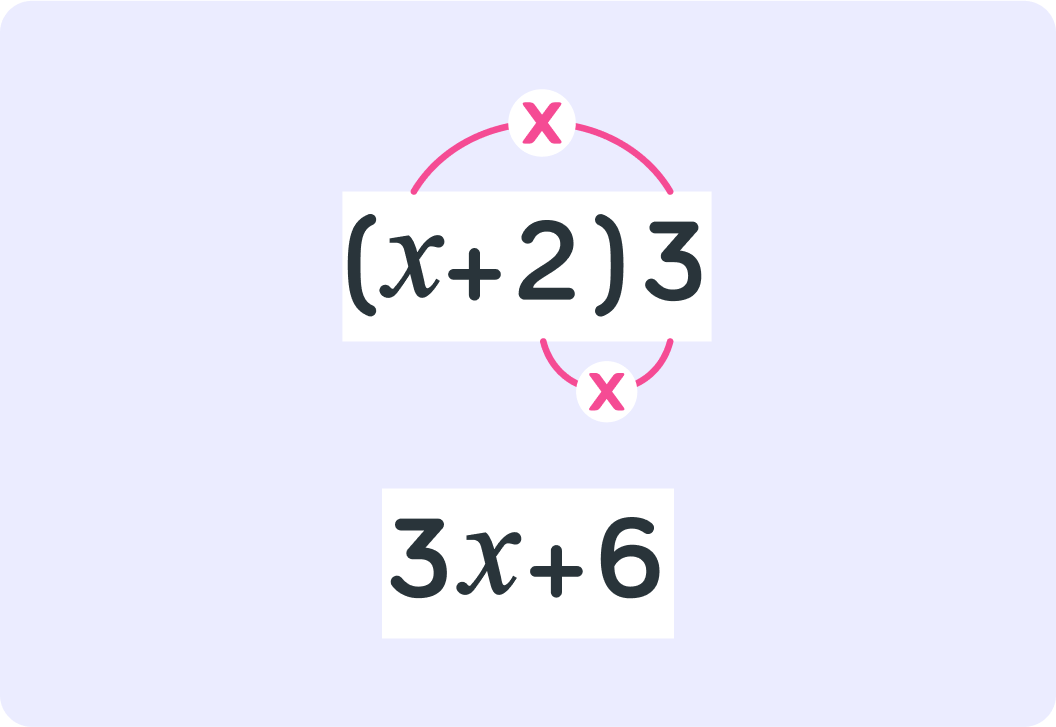
If you multiply a positive and a negative, then remember to keep the minus!

For example, $2 \times -4$ is $-8$ , so this becomes $2x-8$ , not $2x+8$

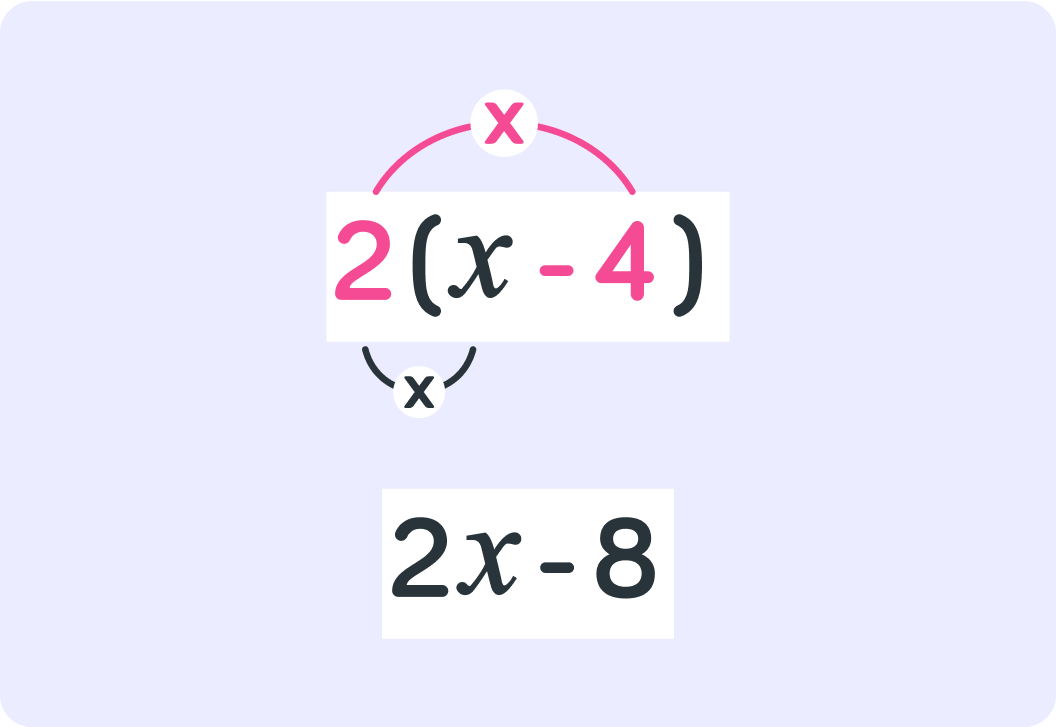
If you multiply $x\times x$ it becomes $x^2$

So if you multiply $x \times 3x$ as in this example, it becomes $3x^2$