Algebra

YOU ARE LEARNING:

Factorising Harder Quadratic Expressions

Factorising Harder Quadratic Expressions

In some quadratic expressions, the coefficient of the squared term is more than one.

Have a look at this example

What is the coefficient for $x^2$ in this quadratic expression?

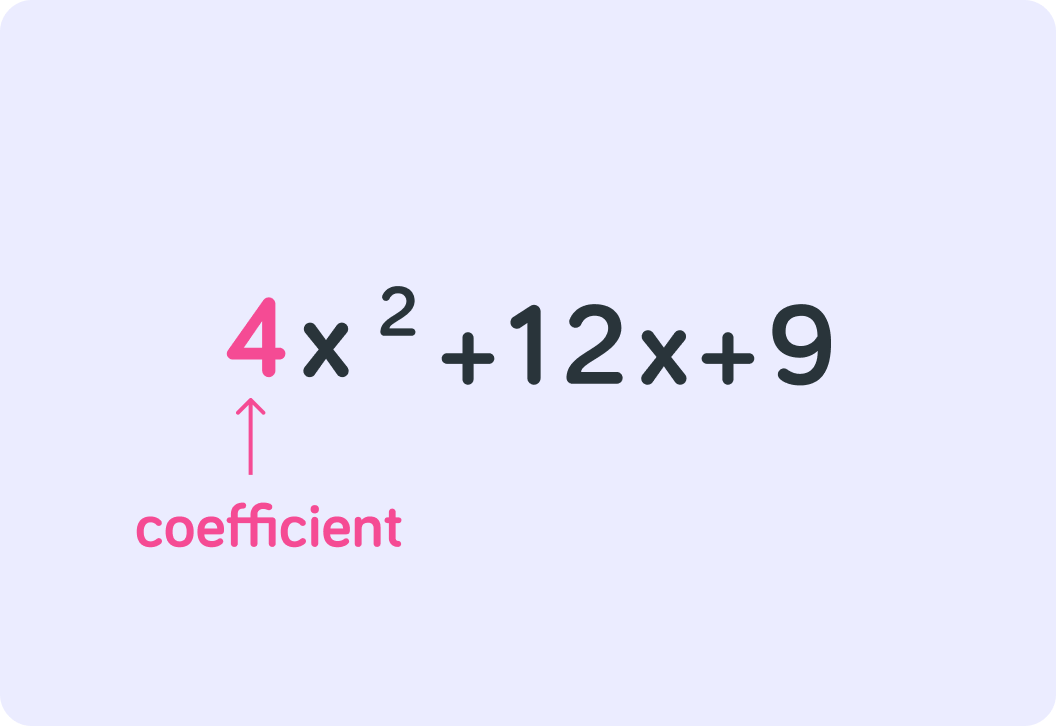
When $x^2$ has a coefficient, you factorise a quadratic expression into the form $(ax+b)(cx+d)$

First you want to find out what $ax$ and $cx$ might be.

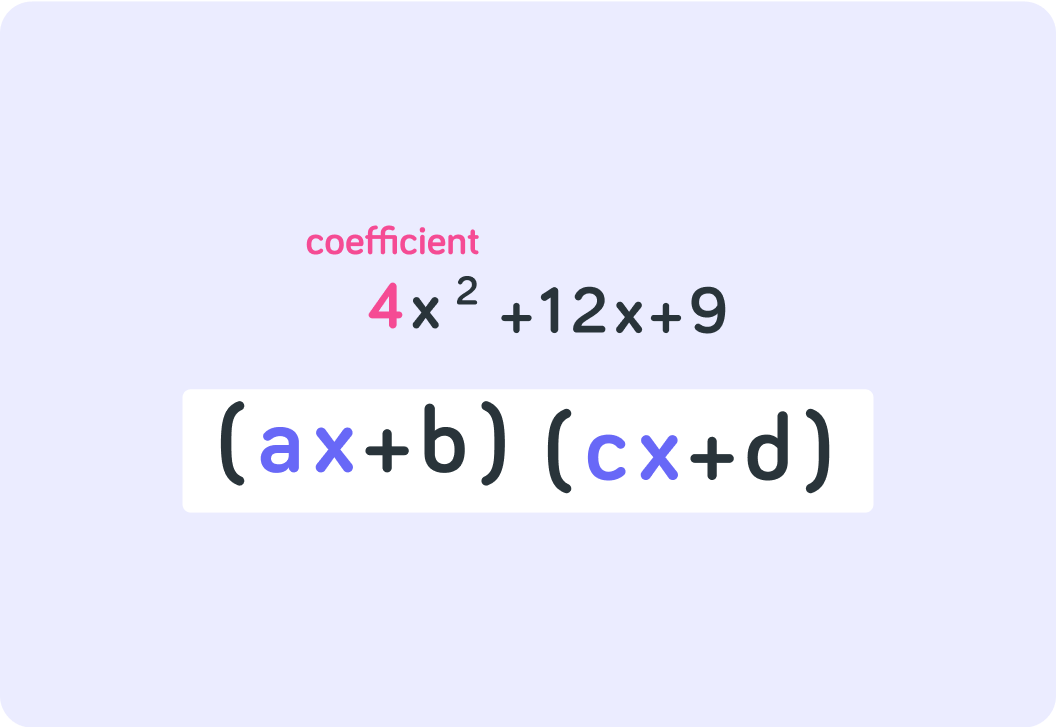
$ax$ multiplied by $cx$ have to give $4x^2$ . Which 2 of these options equal $4x^2$ ?

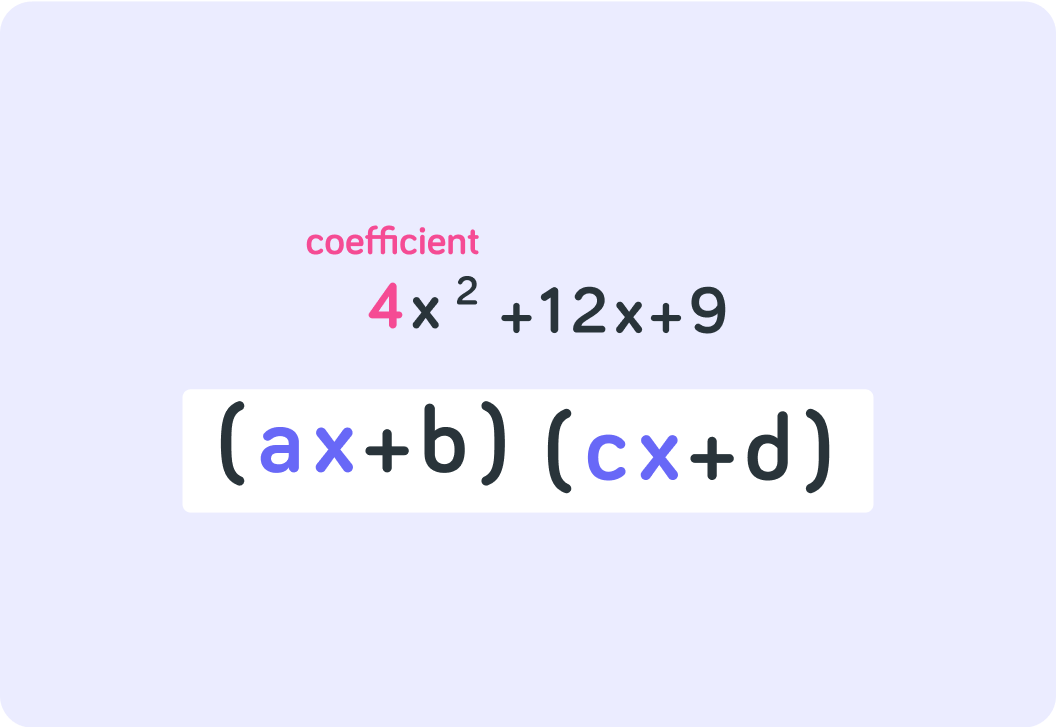
You can select multiple answers

So there are two options for what $ax$ and $cx$ are in the factorised expression

You will come back to finding out which option is the correct one in a minute.

Now you look at $b$ and $d$ . When they are multiplied, they have to equal $9$ . Which 2 of these options fulfil that?

You can select multiple answers

So there are also two options for what $b$ and $d$ are in the factorised expression

That means there are 4 options for what the factorised expression might be!

The correct factorised expression results in $4x^2 + 12x +9$ when you expand the brackets. Which one of the options is that?

So option C is the correct factorisation of $4x^2+12x+9$

The other options don't give you the correct expression when you expand the brackets.

Option A gives you $4x^2+15x+9$

Option B gives you $4x^2+13x+9$

Option D gives you $4x^2+20x+9$

Recap! Sometimes $x^2$ in a quadratic expression will have a coefficient in front of it. There are 3 steps to factorising the expression then.

First you find options for $ax$ and $cx$

If you multiply $ax$ and $cx$ is should equal the first term in the original expression.

Here the first term is $6x^2$ , so the options are $2x \times 3x$ and $6x \times x$

Then you look at options for $b$ and $d$

If you multiply $b$ and $d$ it should equal the last term in the original expression.

Here the last term is $8$ , so the options are $4 \times 2$ and $8 \times 1$

Finally, you can now expand all the options to find out which option is correct

In this example, that is the option where the middle term is $16x$ once you have expanded the brackets and simplified the expression.

What is the correct factorisation of $9x^2+11x+2$ ?

Factorise $2x^2+10x+8$ into the form $(ax + b)(cx+d)$

Now take a look at this example

Here one of the terms is negative

You need to factorise so that you will end up with $-12x$ as the middle term.

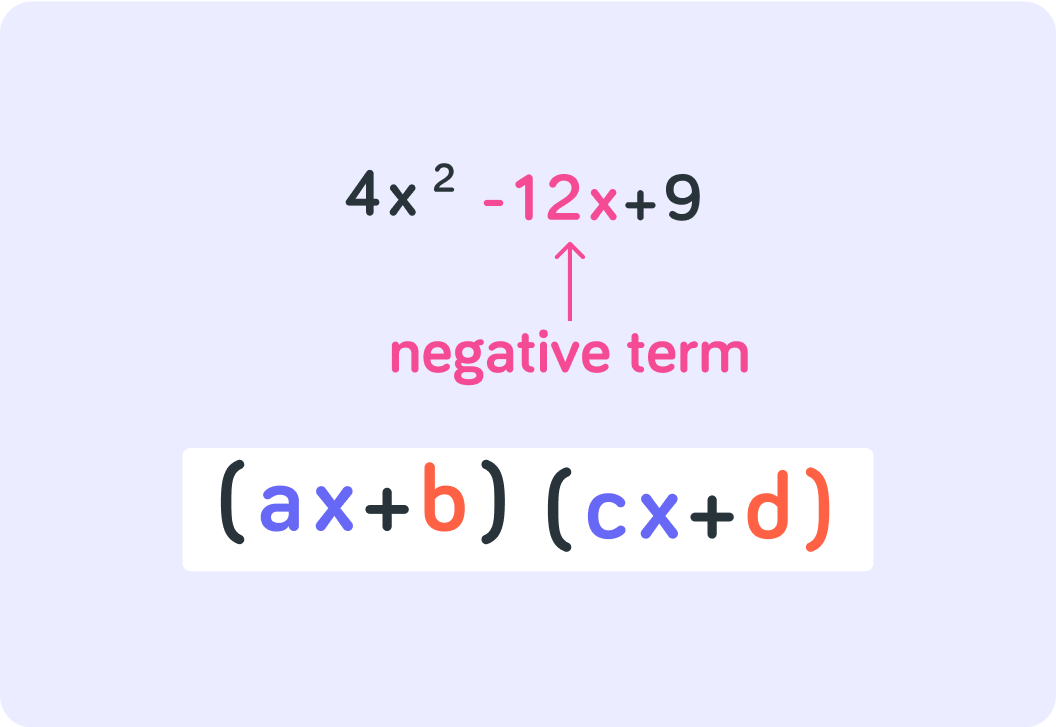
True or false? If $ax$ , $cx$ , $b$ and $d$ are all positive, all terms will also be positive once you have expanded the brackets.

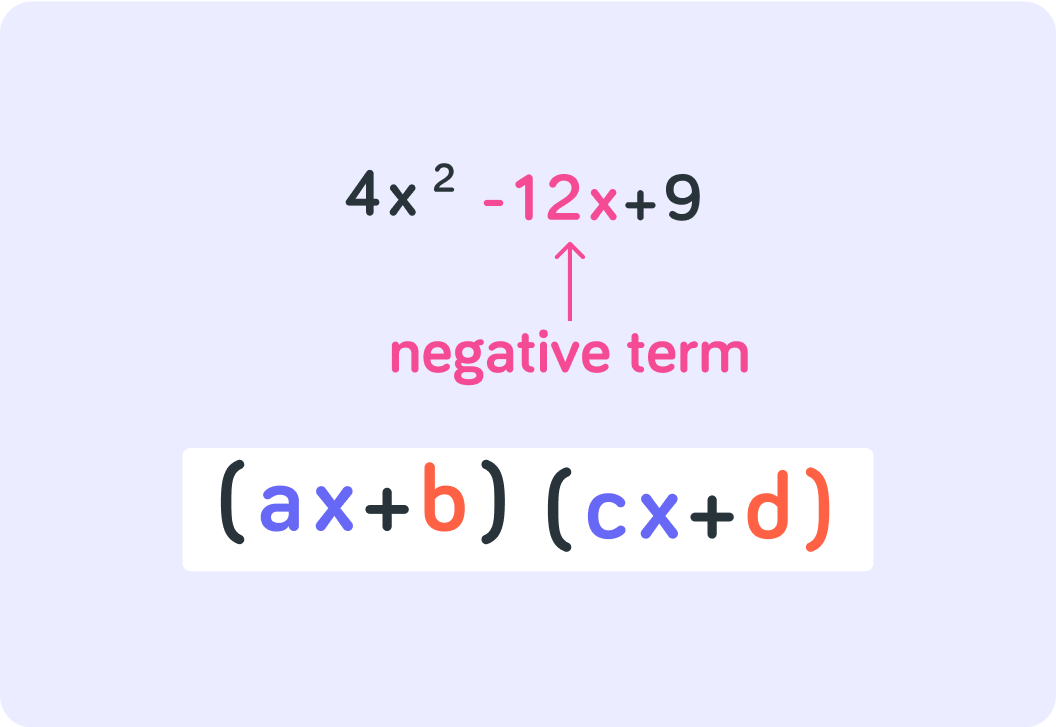
So to get to a negative term when you expand the brackets, at least one of the terms in the factorised expression has to be _____________.

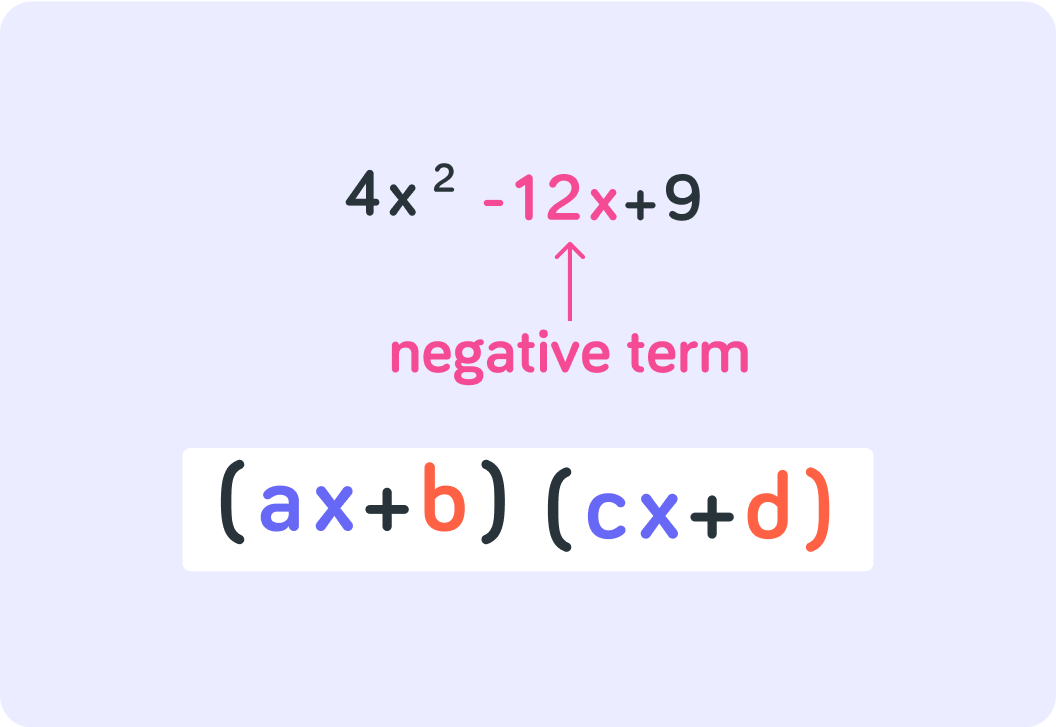
First you find the options for $ax$ and $cx$

They are either $4x \times x$ or $2x \times 2x$

Now, the options for $b$ and $d$ have to make $+9$ when multiplied. Pick all the options below that equal $+9$

You can select multiple answers

So there are actually 4 options for $b$ and $d$

Two pairs of positives and two pairs of negatives.

You could also write the options as $\pm 3 \times \pm3$ and $\pm9 \times \pm1$ to save space.

You can exclude two of these pairs as correct options for $b$ and $d$ . Which ones?

So now you are down to two options for $b$ and $d$ . That gives you 4 options for factorised expressions. Which one is the correct one?

So when one of the terms in the original expression is negative, at least one of the terms in the factorised expression has to also be negative

Here both $b$ and $d$ are negative, because when they are multiplied they have to give the positive number $+9$

What is the correct factorisation of $6x^2+19x-7$ ?

Factorise $5x^2-22x+8$ into the form $(ax + b)(cx+d)$

Summary! There are 3 steps to factorising these harder quadratic expressions where there is a coefficient in front of $x^2$

First you find options for $ax$ and $cx$

If you multiply $ax$ and $cx$ is should equal the first term in the original expression.

Then you look at options for $b$ and $d$

If you multiply $b$ and $d$ it should equal the last term in the original expression.

Finally, you can now expand all the options to find out which option is correct

In this example, that is the option where the middle term is $-22x$ once you have expanded the brackets and simplified the expression.

When one of the terms in the original expression is negative, at least one of the terms in the factorised expression has to also be negative

If you only have positive terms, all terms will be positive when you expand the brackets.