Algebra

YOU ARE LEARNING:

Linear Inequalities 1

Unlike an equation, inequalities can have a range of values as solutions.

Unlike equations, inequalities specify a particular set of values as the solution, rather than one or two specific values.

It involves using some symbols instead of the = sign.

$5>3$

This means that 5 is greater than 3. Notice that the larger end of the $>$ is with the larger number, 5.

$10<20$

This means that 10 is less than 20. Notice that the smaller end of the $<$ is with the smaller number, 10.

What does $x<10$ mean?

We also find these symbols in algebra, indicating that there are a range of solutions.

Let's try solving $x + 5 < 6$ to find $x$

Look at the symbol

It shows that $x+5$ is less than $6$ . We can treat this in the same way as an equation, and subtract 5 from both sides to isolate $x$ .

Subtract 5 from both sides

The solution is $x<1$

Therefore, $x$ can be any value less than 1.

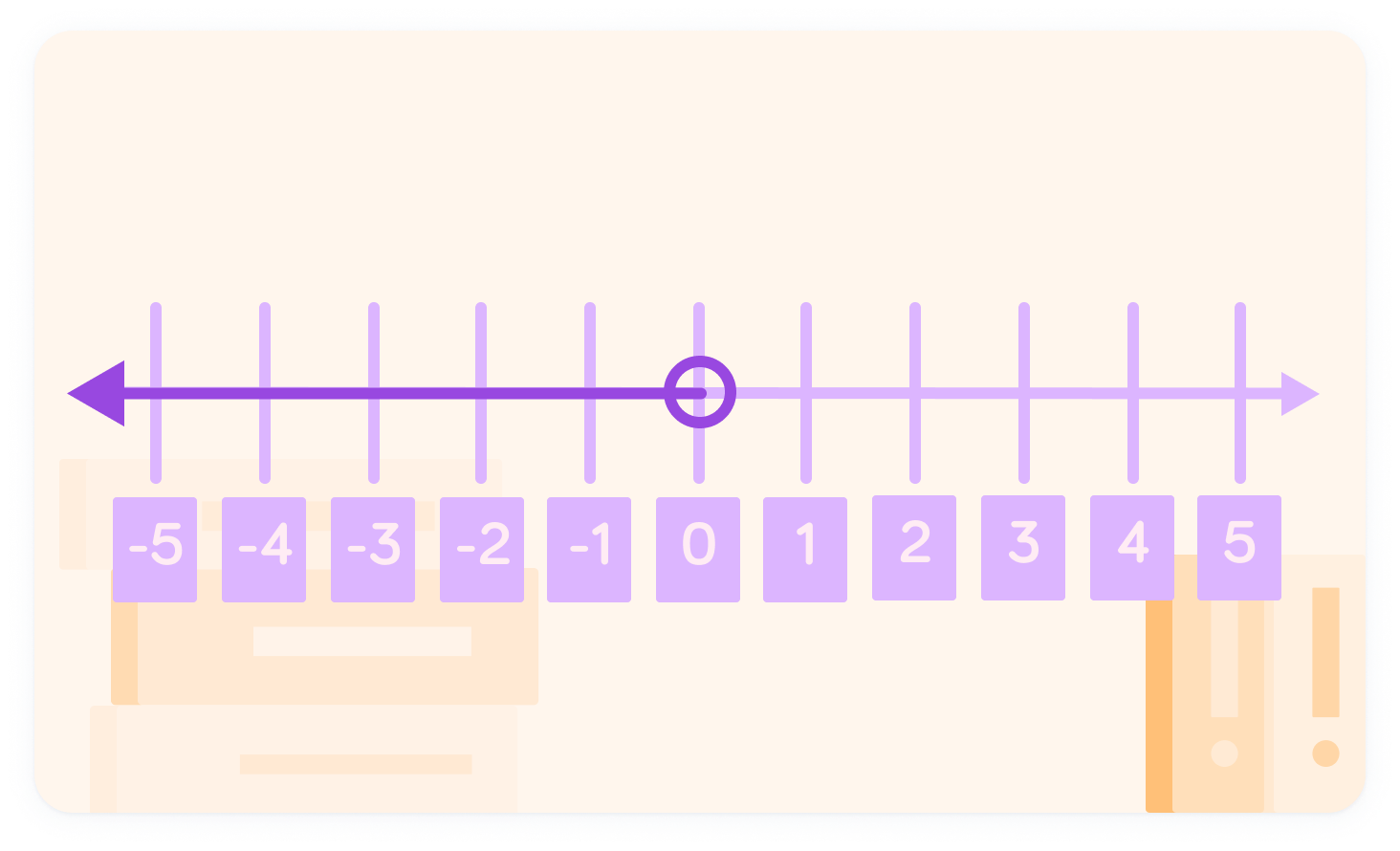
We can display $x<1$ on a number line

$x$ can be any value less than 1. The OPEN circle at 1 indicates that the inequality does not include 1.

Solve $x -7 > 10$

Solve $5 + x \leq -2$

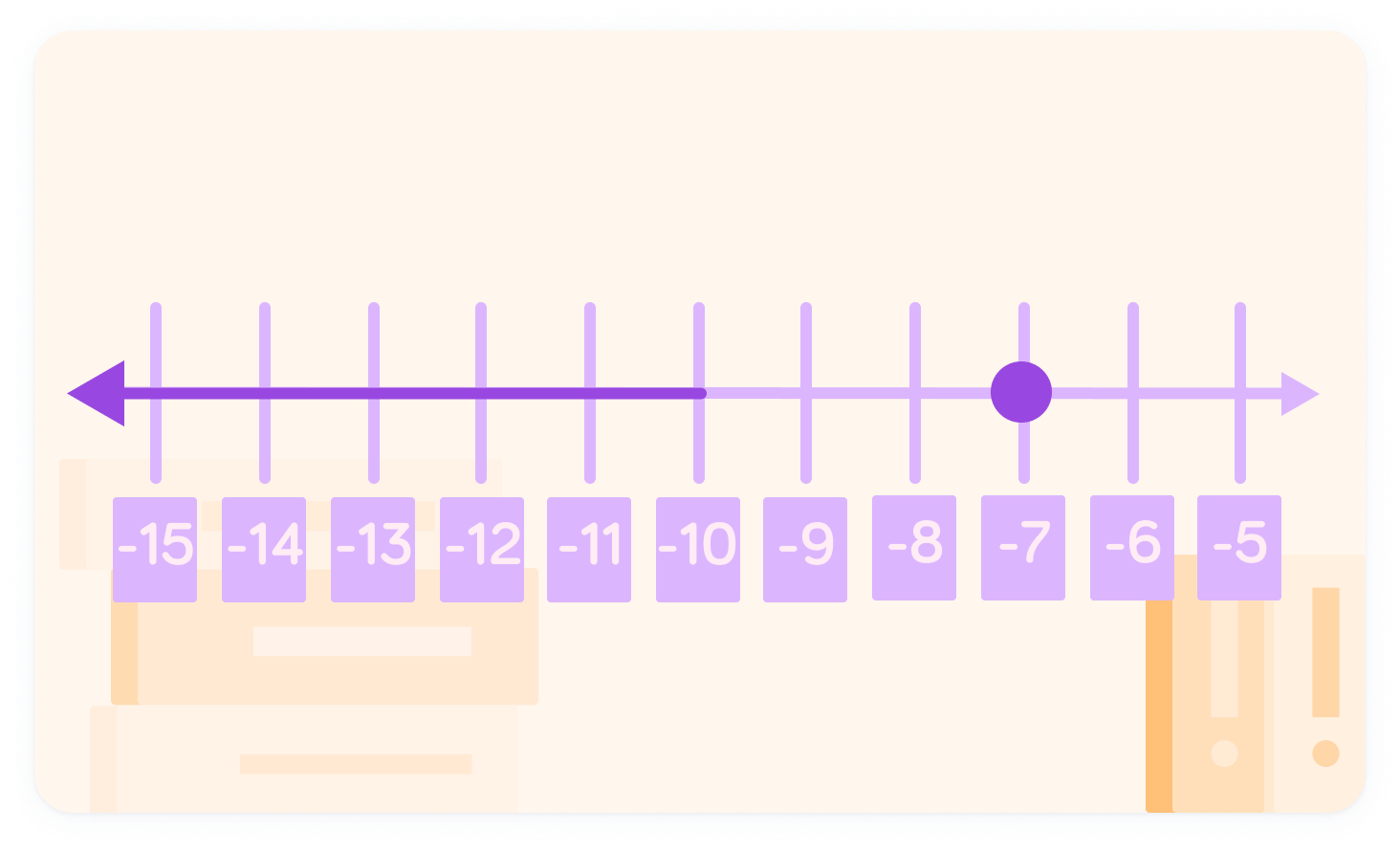
We can also display $x\le-7$ on a number line

This time, the filled circle indicates that the inequality does include $-7$ .

Great work! 🙌

Most of the ways you manipulate equations work for inequalities, except for division by a negative number. In this case, you have to reverse the direction of the inequality sign.

For example: $3 - x < 5$

As normal, subtract 3 from both sides

$-x < 2$

We have $-x$ , but we need $x$

We need to divide by a negative number to get $x$ . This means that we need to switch the direction of the inequality sign.

Divide by -1 and switch the sign

$-x < 2 \space \space\space \space \rightarrow \space \space \space \space x > -2$

Solve $4 - 2x < 10$

Try another one! $17 < 5 - 3x$