Linear Inequalities 2

$3<2x+5$

$2x+5<11$

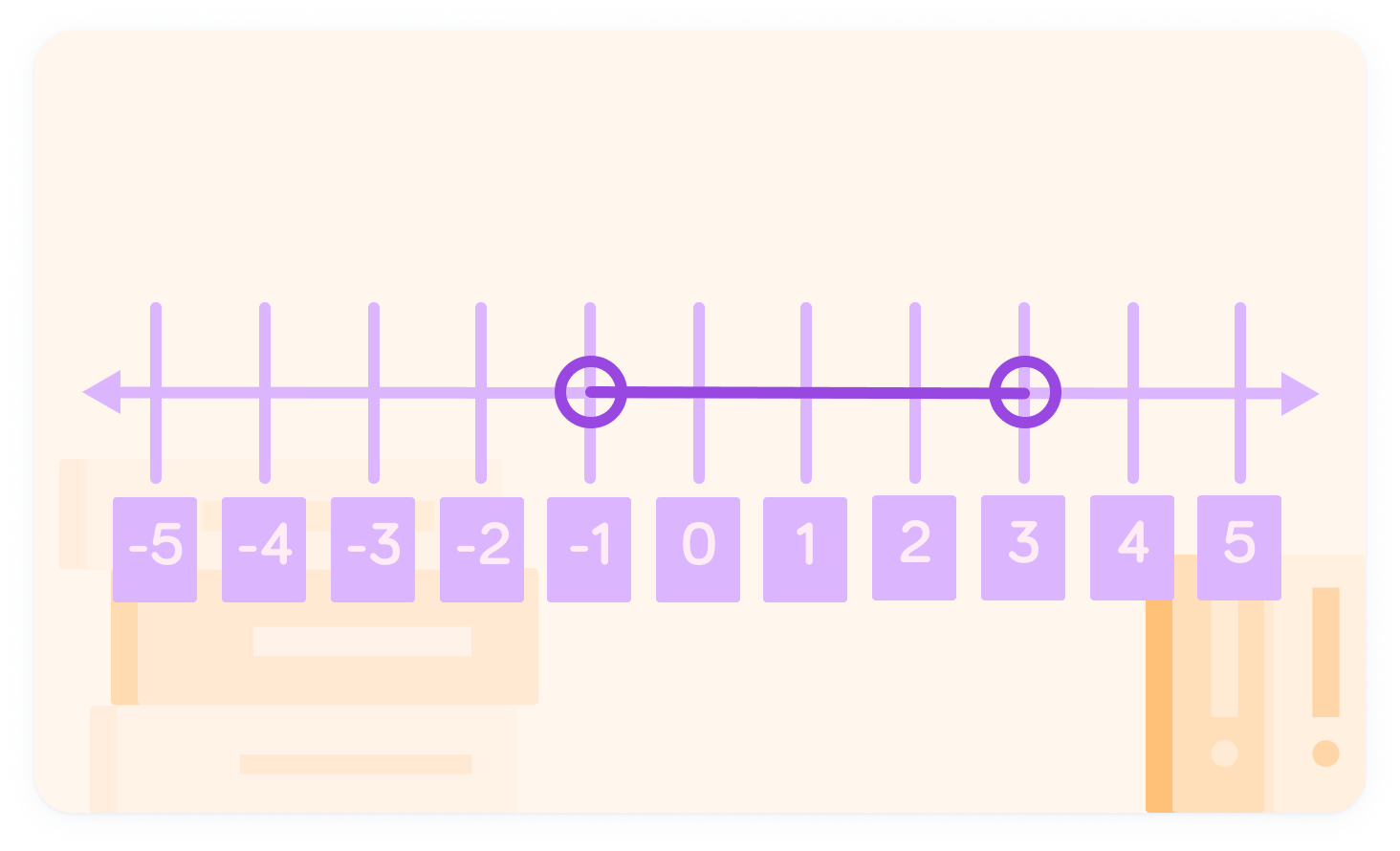
Our individual inequalities give the answers $x<3$ and $x>-1$. We can combine these into a single inequality, so the final answer is $-1 < x < 3$.

The open circle indicates that the inequality does not include -1 or 3.

This involves using the smallest value of each variable.$x=1$ and y=2$$y=2\rightarrow$$y=2\rightarrow1+2=3

Now we need to choose the largest values of each variable.$x=9$ and y=8$$y=8\rightarrow$$y=8\rightarrow9+8=17

Each of the other values of $x+y$ will be between the upper and lower bounds.

The upper bound is 17, so $x+y\le17$. The lower bound is 3, so $3\le x+y$. We can arrange these two inequalities into a single inequality$3 \leq x + y \leq 17$

Have a look at the values given in the question. Does this inequality seem possible? It looks like it is, so we can confirm this is the final answer!