Geometry

YOU ARE LEARNING:

Area of Circles

We can use a special constant called pi to find the area of a circle of any size.

Circles are quite special shapes, mathematically. Formulae for the perimeter and area make use of a number referred to as pi, which is a Greek letter pronounced “pie”.

The circumference of a circle is its outer edge. Each point on the circumference is equal distance from the centre. Let's refresh on a few key lines on a circle.

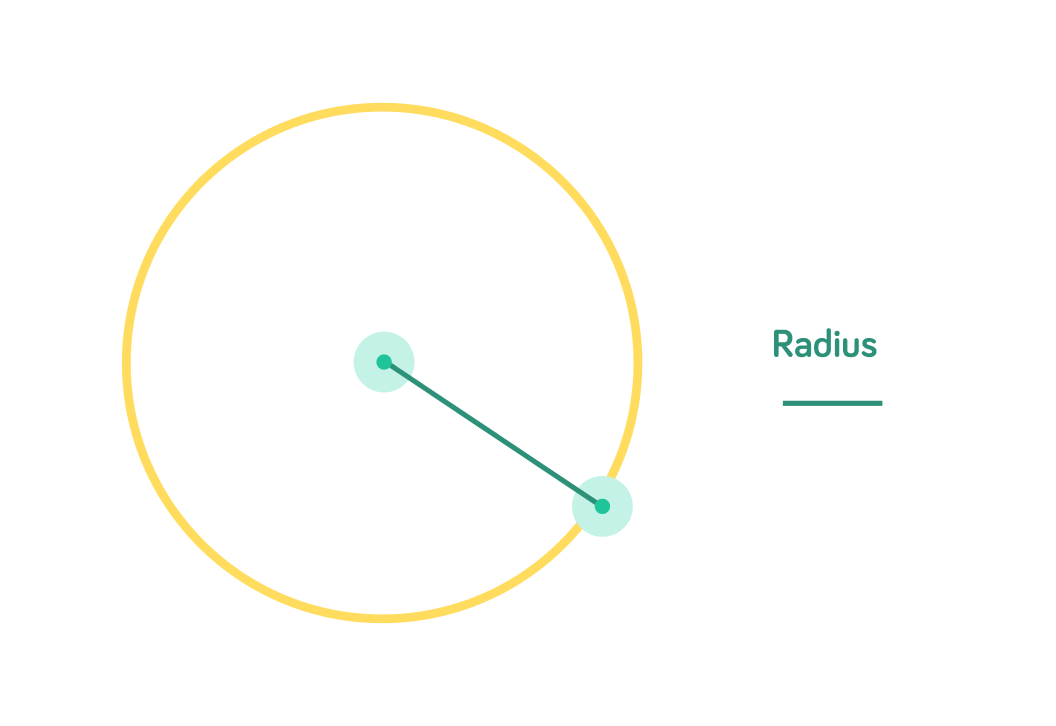
This is the radius

The radius is the length between the centre of the circle and any point on the circumference of the circle.

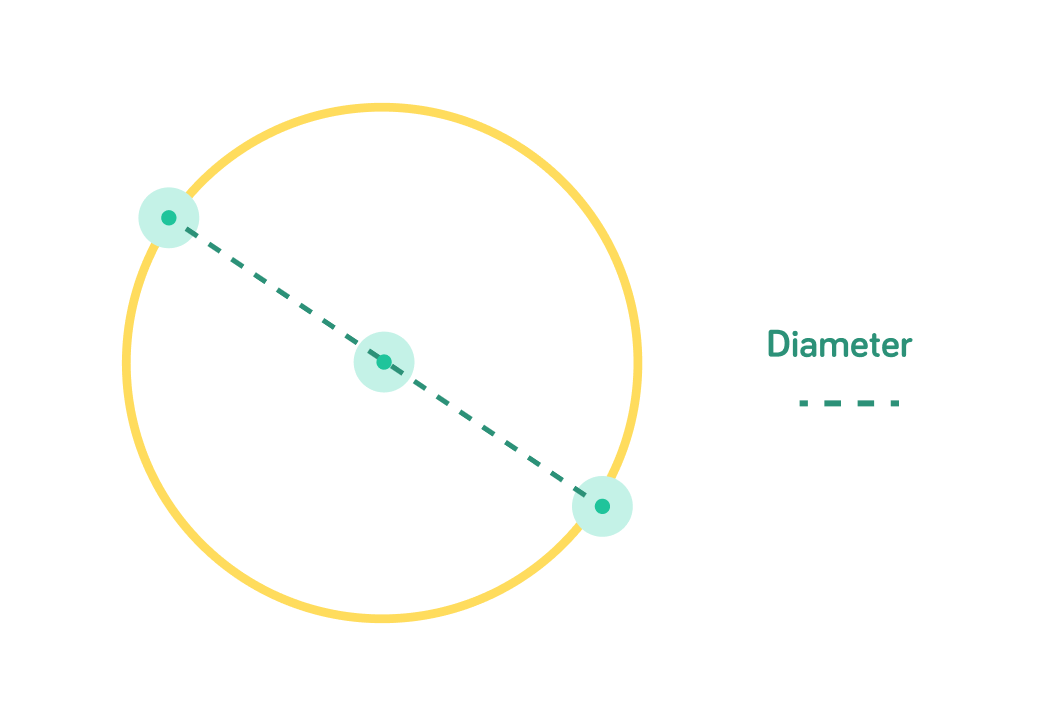
This is the diameter

The diameter crosses through the centre of the circle, and connects two points on the circumference. Therefore, it is also twice the radius.

Which line is this?

How much longer is the diameter of a circle compared to the radius?

Pi is defined as the ratio between a circle's circumference to its diameter. This means that the circumference is pi times bigger than the diameter. We represent pi with the symbol $\pi$ . Pi is: $3.14159265359$

We can use this formula to find the circumference

In this formula, $d$ is the diameter.

We can use the radius to find the circumference

Since the radius is twice the diameter, we can multiply the radius by 2 and multiply it by $\pi$ to find the circumference.

We can find the area of a circle using this formula

The $\pi$ relationship we have learned also allows us to find the area of a circle given its radius.