YOU ARE LEARNING:
Circle Theorems: Angle in a semi-circle

Circle Theorems: Angle in a semi-circle
We can apply universal rules to solve geometrical problems involving circles, where there are tangents, secants or chords present.
The properties of circles have been been studied for centuries, and there are a range of generalised results which are true for circles of any size.
First, let's define some lines!
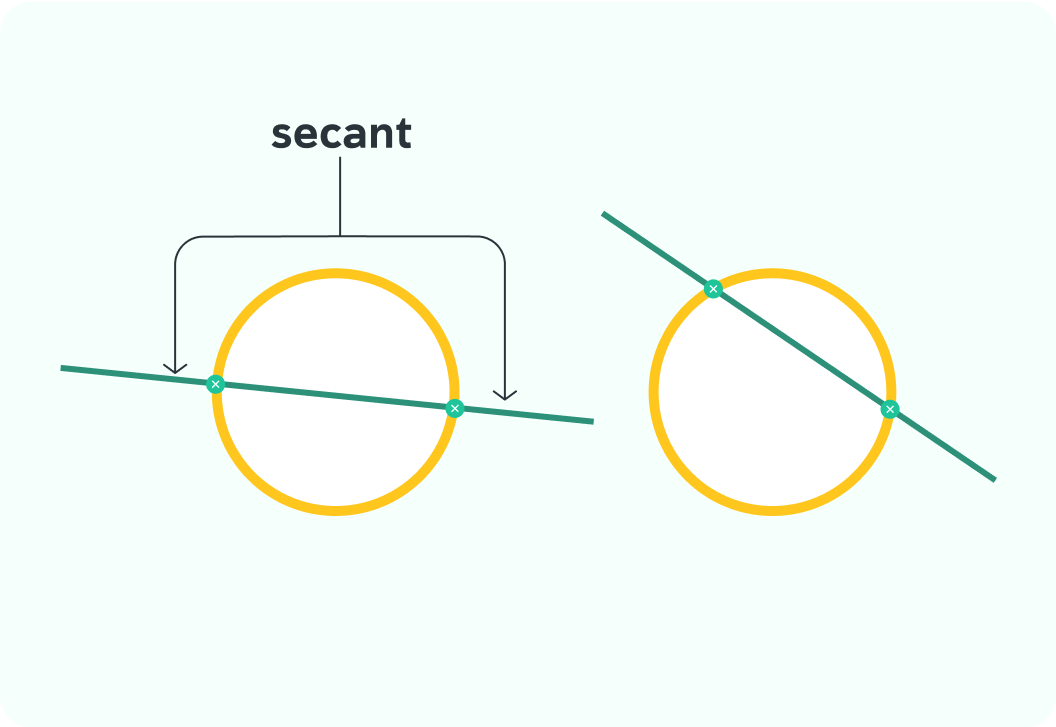
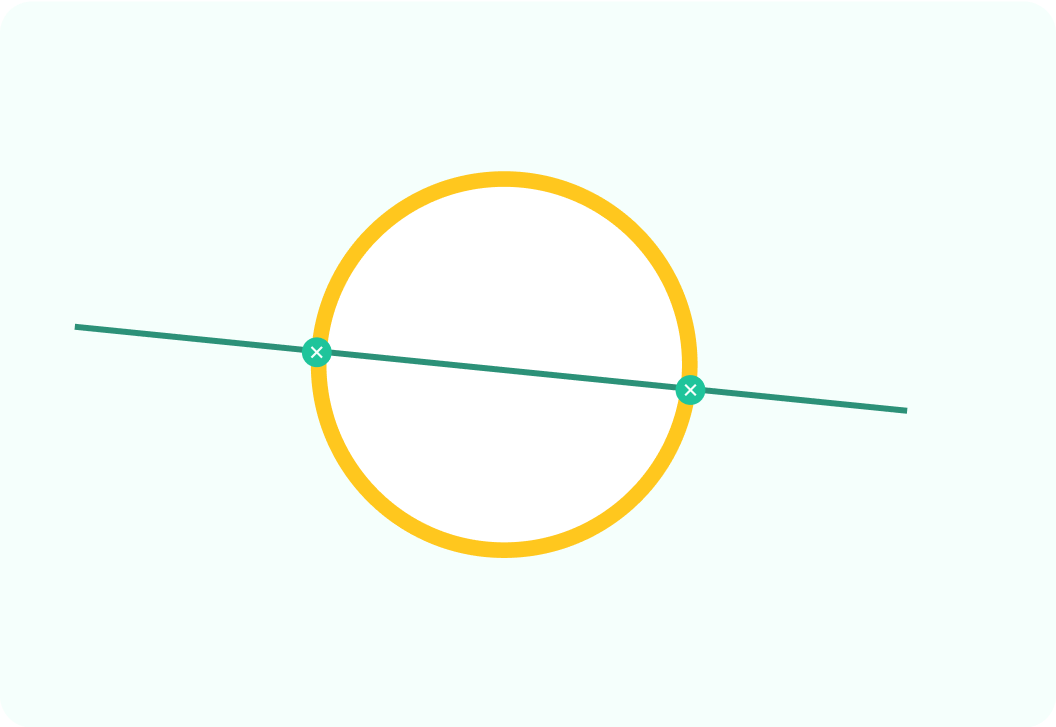
This is a secant
A secant moves through two points on the circumference of a circle, and keeps going
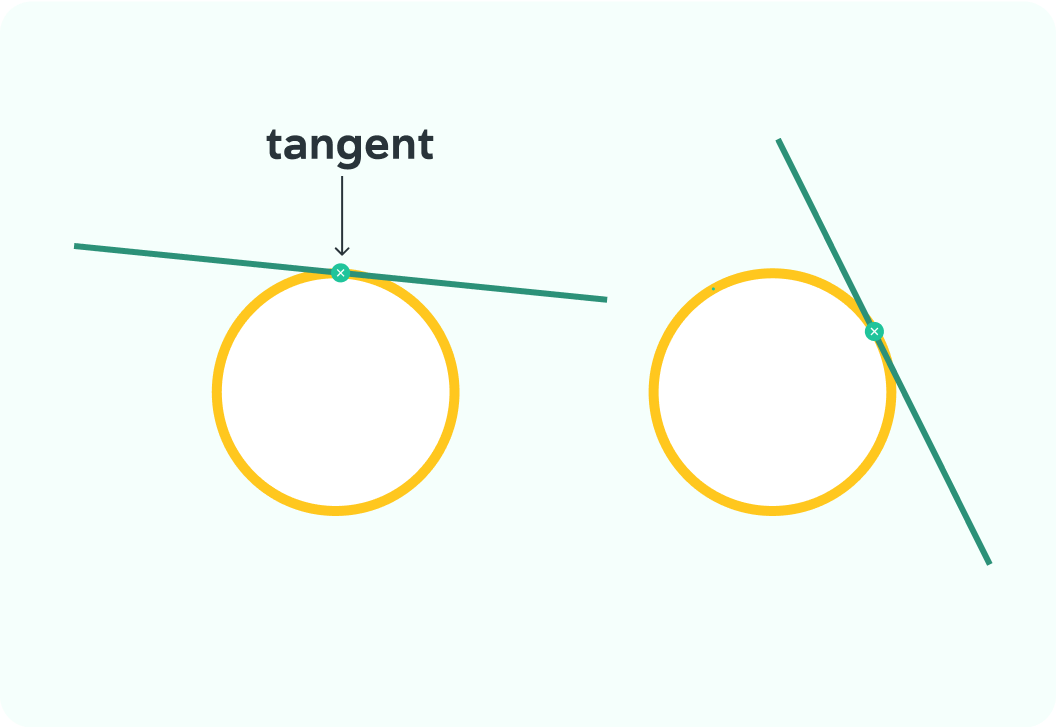
This is a tangent
A tangent touches the circumference of a circle at a single point
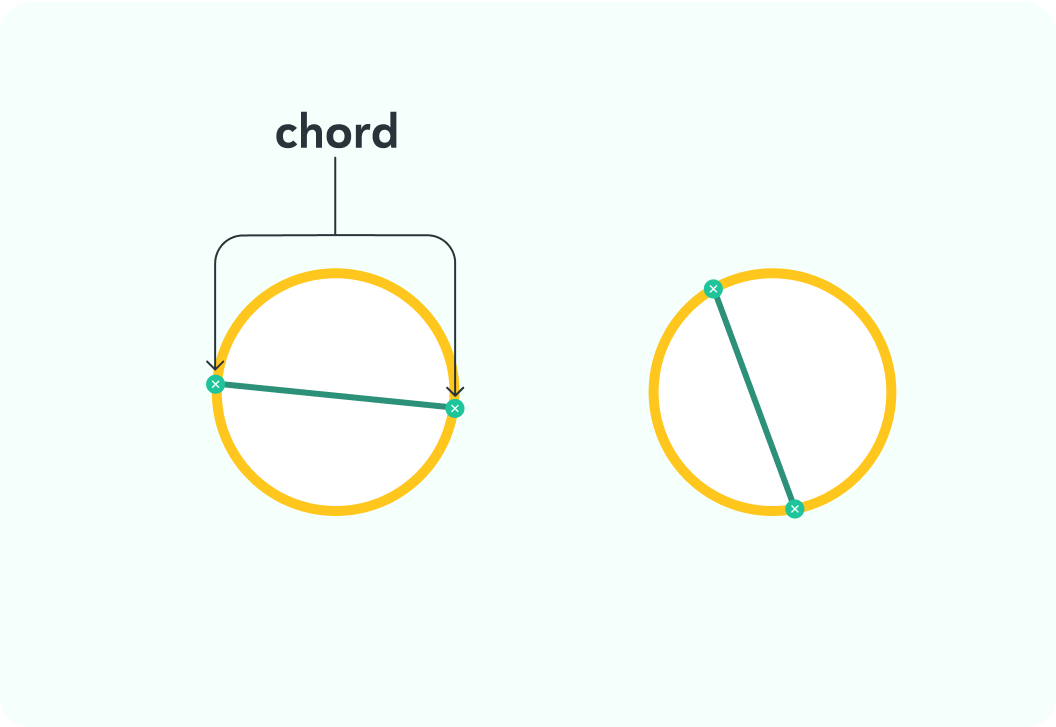
This is a chord
A chord is a straight line which connects any two points on the circumference of a circle
What type of line is this?

Let's go through the first two circle theorems!
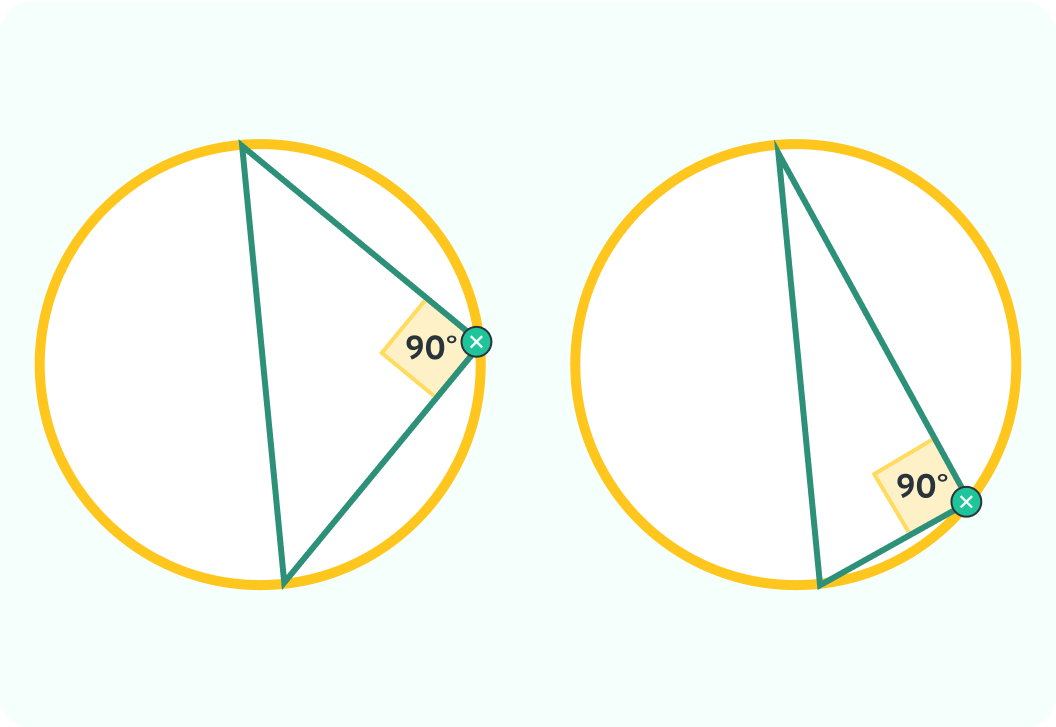
The angle in a semicircle is 90°
The line moves through the centre of the circle. No matter where you move the yellow point, the angle is always 90°!
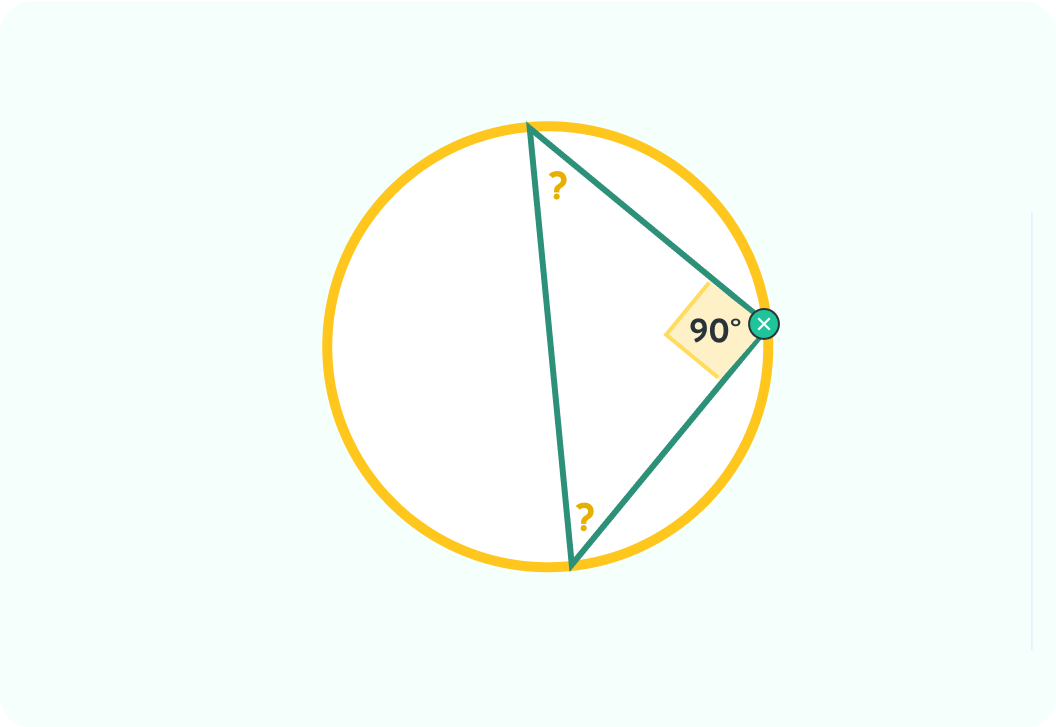
What is the sum of the other two angles in this triangle?

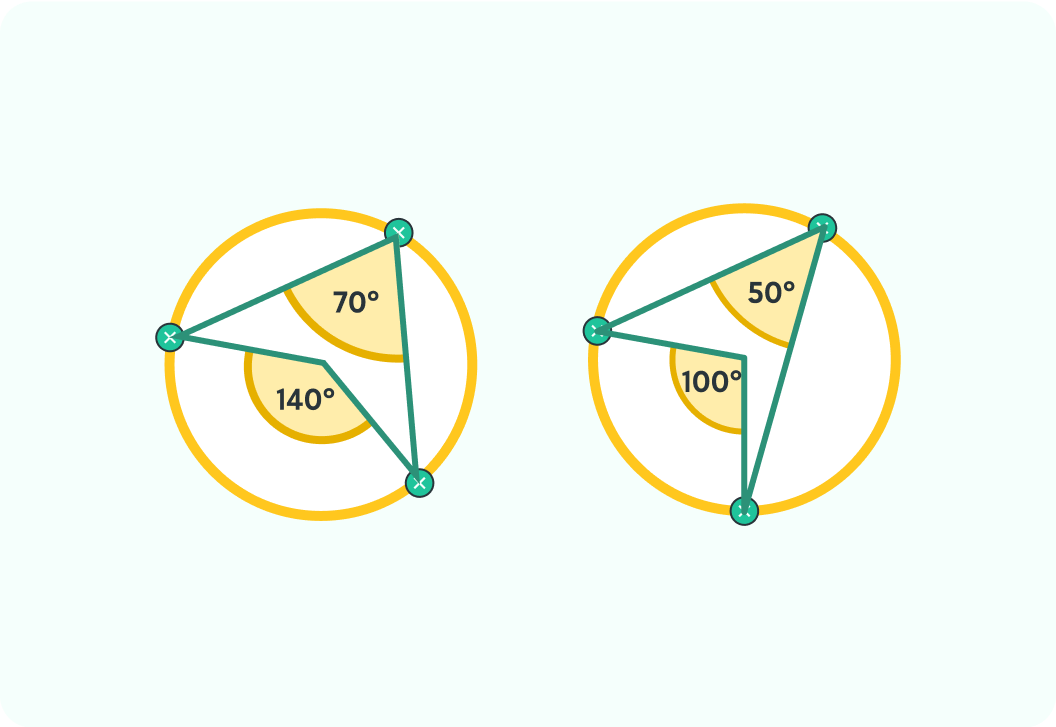
The angle in the centre is twice the angle at the circumference
By drawing two radii and two chords, we form a situation where there are two angles. Try dragging around the green points - the angle in the centre is always twice the angle at the circumference.
What would the angle at the circumference be here? Write the number of degrees.

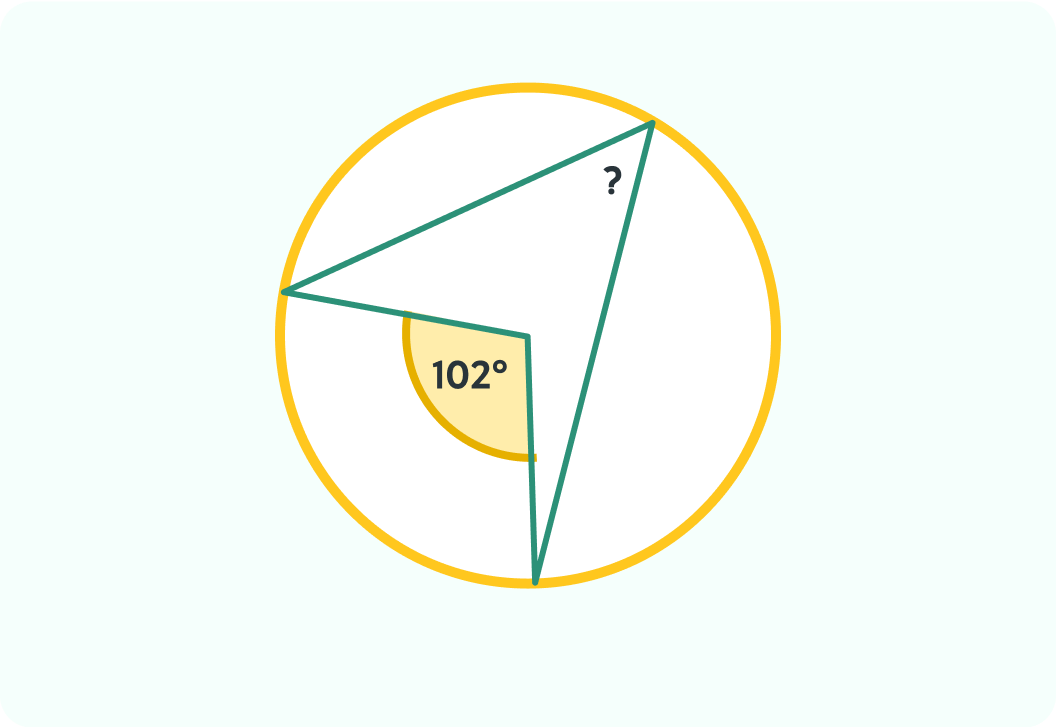
The angle at the circumference is 51°
This is because the angle would be half the angle at the centre, so 102°÷2=51°
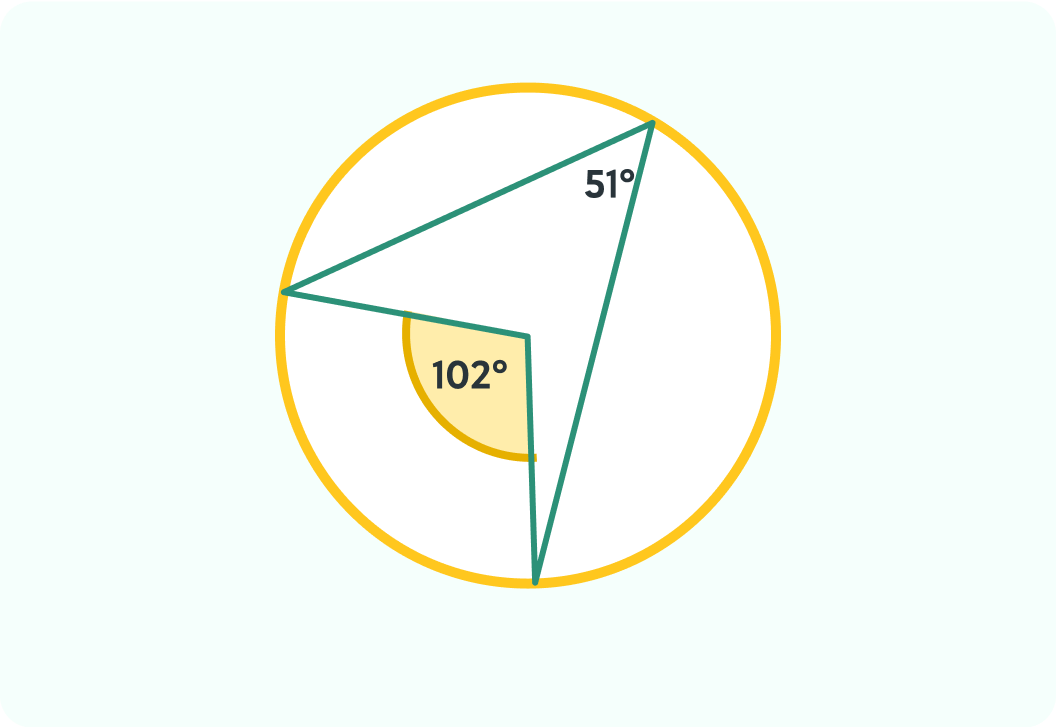
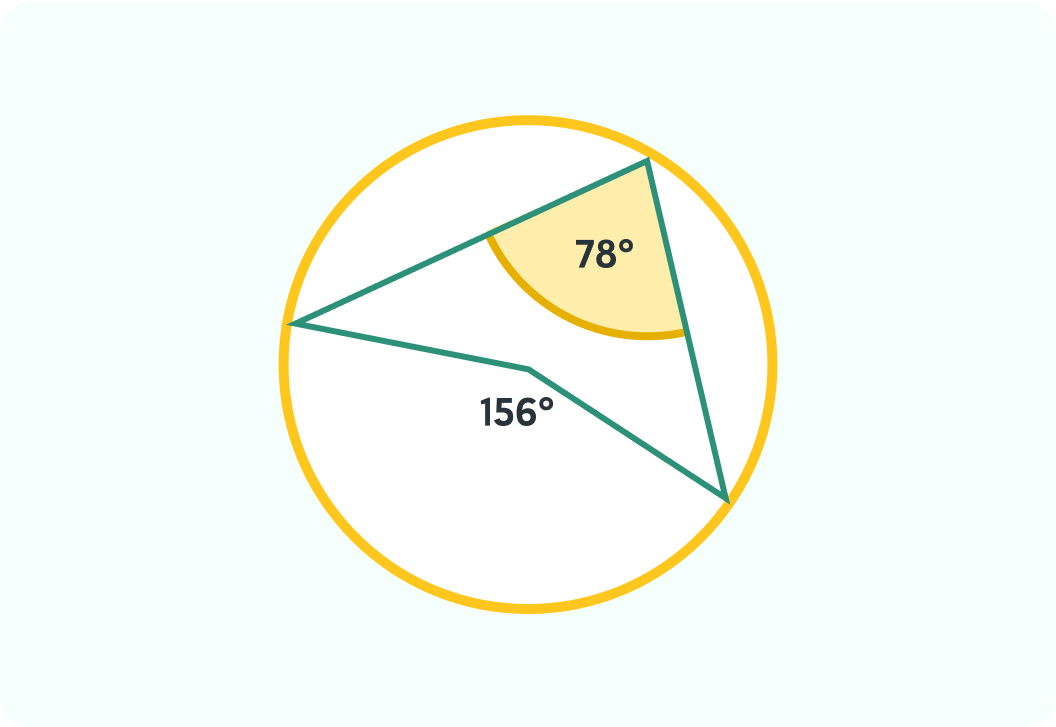
What is the angle at the centre here? Write the number of degrees.

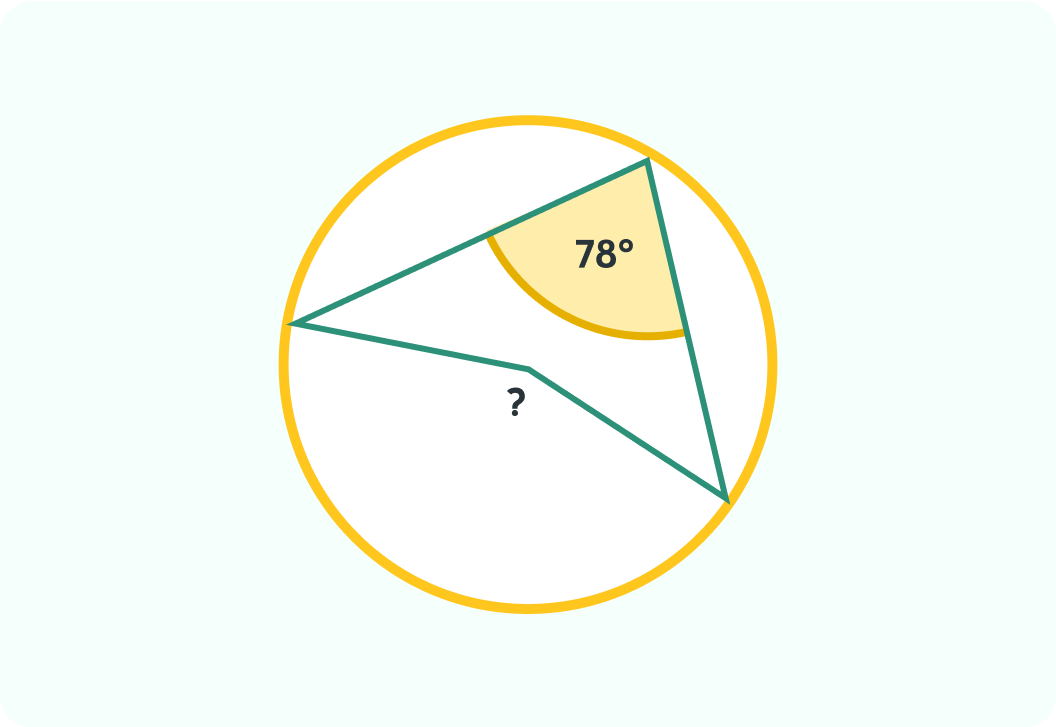
The angle is 156°
This is because the angle in the centre is double the angle at the circumference, so 78°×2=156°