Geometry

YOU ARE LEARNING:

Perimeter and Area

The area and perimeter of shapes are fundamental properties which we come across in every day life.

Area and perimeter are important spatial properties to understand, as you will see them in many areas of life. For example, the size of a house is often measured by area, while you may measure the size of clothing by perimeter.

Area is the space enclosed by a shape, whereas perimeter is the distance around it.

Calculating the perimeter simply requires us to add up the distances of each side.

Finding the area is dependent on the particular shape you are looking at. We can use specific formulas for each type of shape.

This is the formula for a rectangle

Once we know the two side lengths (opposite sides are equal in length in a rectangle), we can find the area.

We can use the same formula for a parallelogram

A parallelogram is also known as a rhombus. The trick here is to find the height, rather than the diagonal side length.

The units for area are squared. This is because the area accounts for two dimensions, base and height. If the lengths are given in centimetres, then the area units are $cm^2$ . If they are given in metres, then the area units are $m^2$ .

What are the units of area if the lengths are given in millimetres?

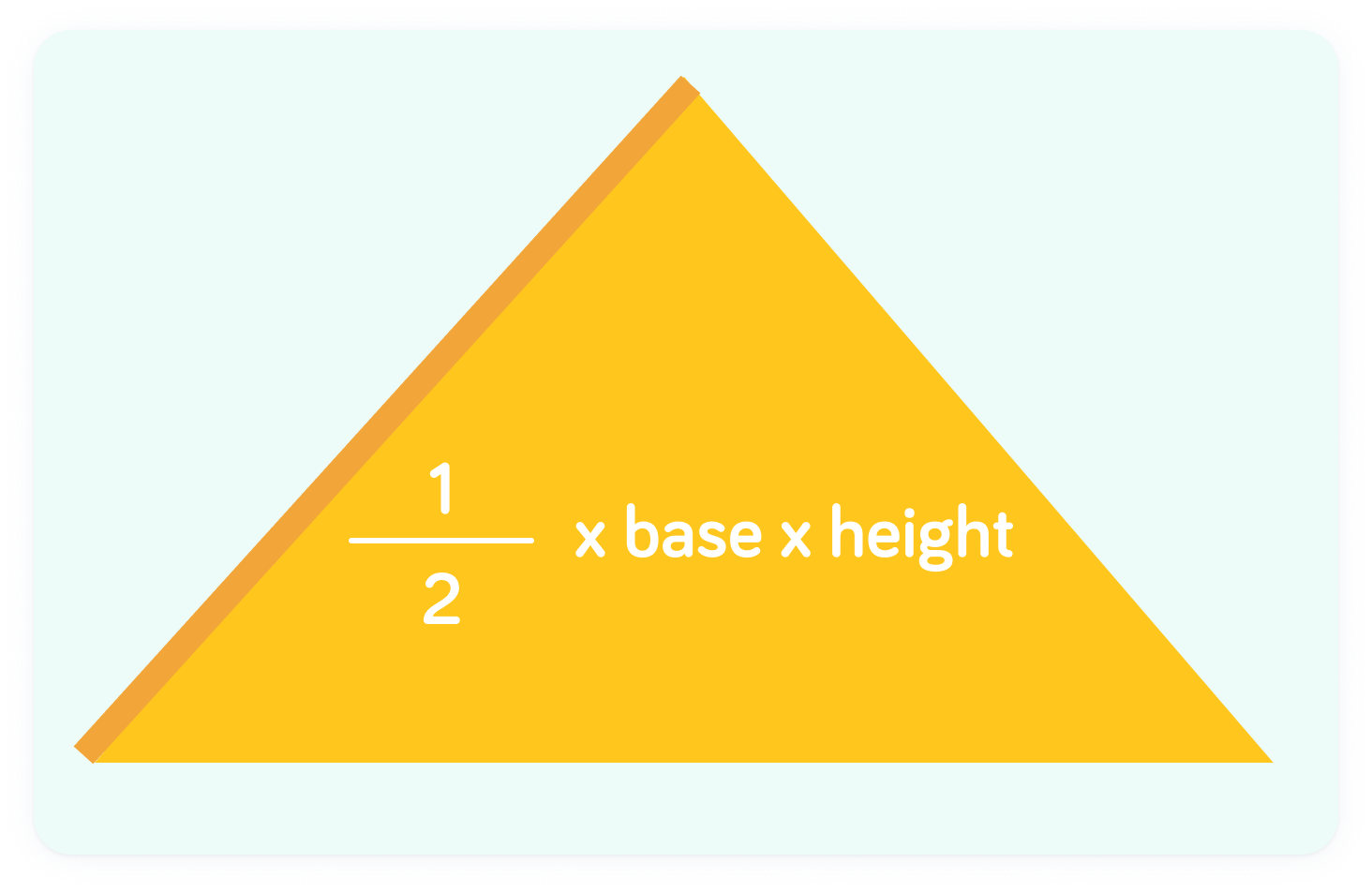
This is the area formula for a triangle

The key here is to remember that a triangle takes up half the space of the rectangle which could be made by joining up each of its corners.

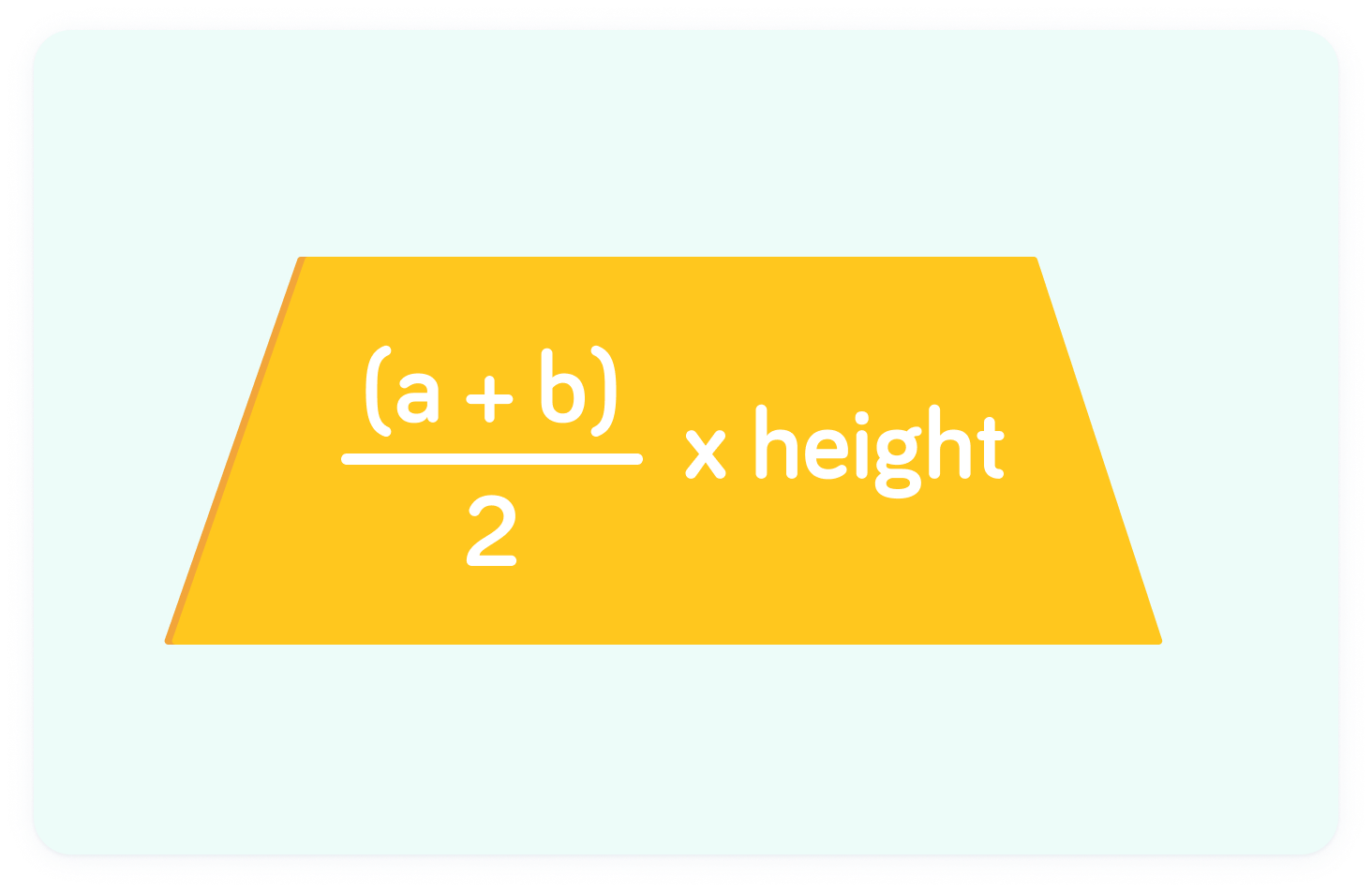
This is the formula for the area of a trapezium

$a+b$ indicates the sum of the parallel sides. We can multiply half of this sum by the height to find the area.