Geometry

YOU ARE LEARNING:

Spheres: Volume and Surface Area

Spheres: Volume and Surface Area

Spheres require specific formulae to find their volumes and surface area.

As well as prisms, there are other special 3D shapes that have specific formulae. These include spheres, cones and pyramids.

This is the formula for the volume of a sphere

$r$ is the radius. We can use this for a sphere of any size.

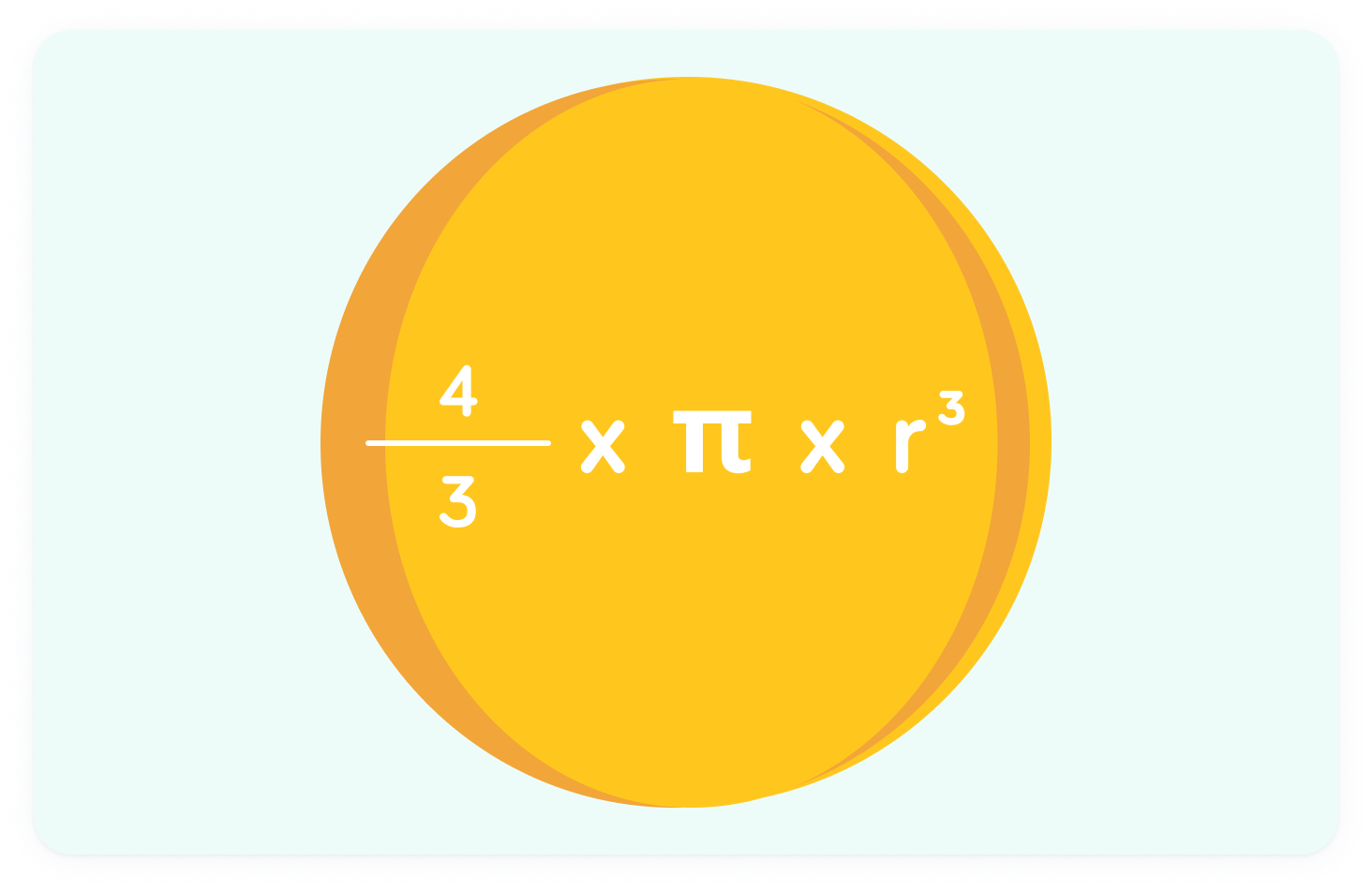
What is the volume of a sphere, of radius $9cm$ , in terms of $\pi$ ?

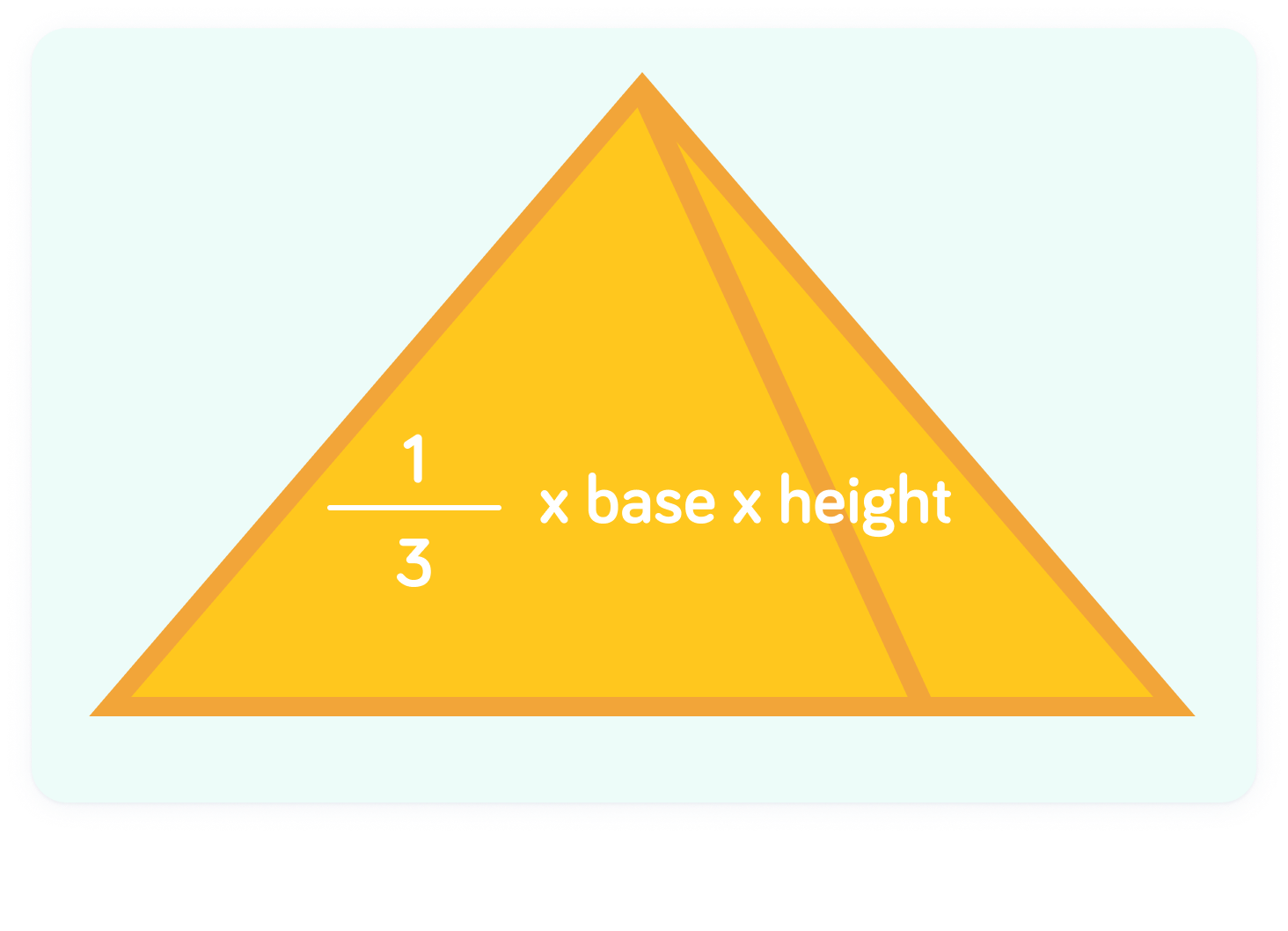
This is the formula for the volume of a pyramid

A pyramid takes up $\dfrac{1}{3}$ of the space compared to the cuboid which joins each of its vertices together. Notice that this is similar to the area, but there is an extra dimension involved.

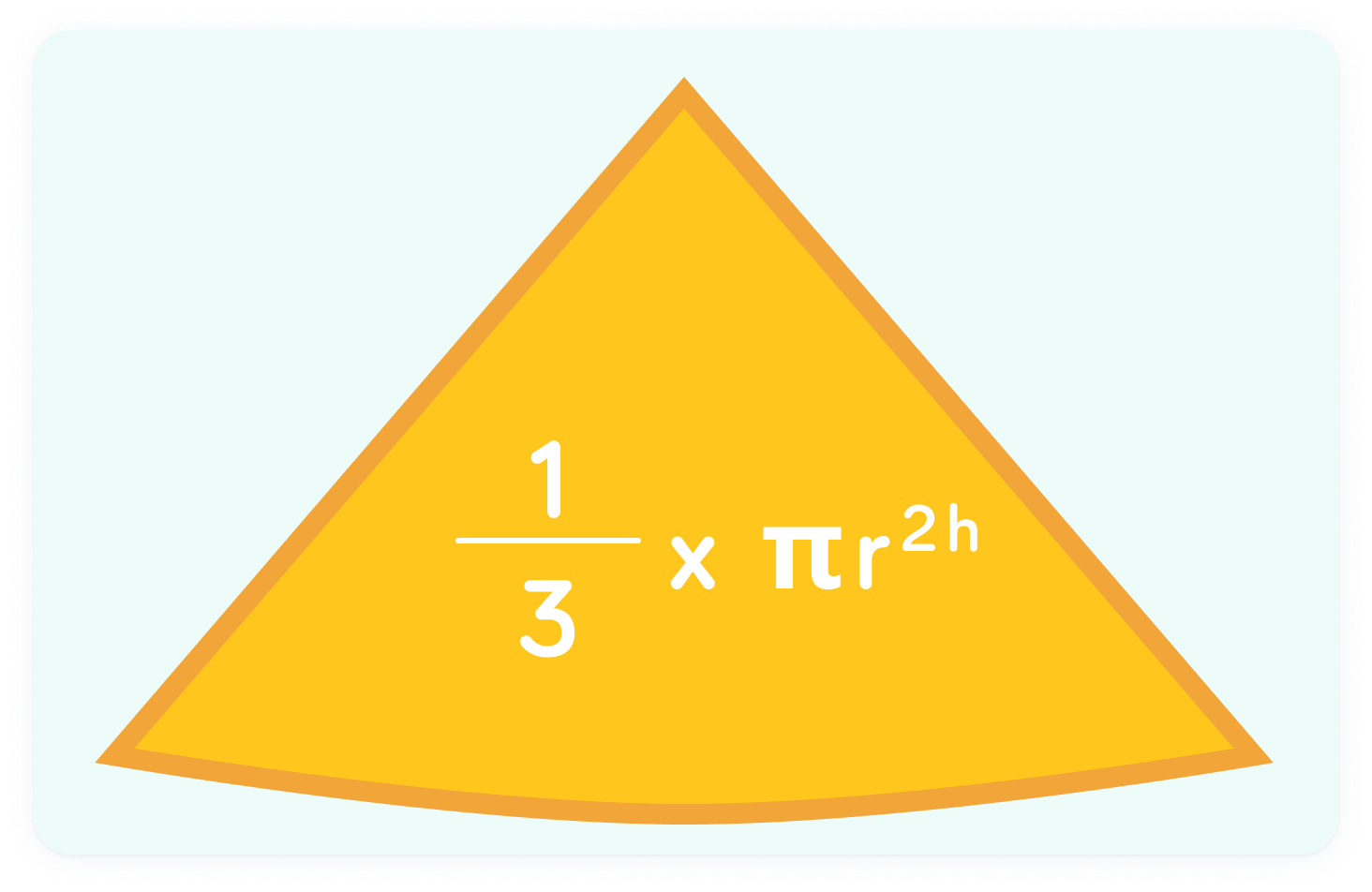
Similarly, this is the formula for the volume of a cone

Notice that this is essentially the same. $\pi r^2$ is the area of the circular base and $h$ is the height, measured vertically from the base to the top of the pyramid. The $\dfrac{1}{3}$ accounts for the thinning near the top.

Given that a cone has a volume of $100 \pi m^3$ and a height of $12m$ , what is its radius?

First, put the values you know into the formula

$V = \dfrac{1}{3} \pi r^2h \rightarrow 100\pi = \dfrac{1}{3} \pi \times r^2 \times 12$

Simplify the equation

$100\pi = \dfrac{1}{3} \pi \times r^2 \times 12 \rightarrow 100\pi = 4\pi r^2$

Rearrange the equation to make $r^2$ the subject

If $r^2=25$ , what is $r$ ?