Geometry

YOU ARE LEARNING:

The Sine Rule: Finding Sides

The Sine Rule allows us to find unknown angles and sides in non-right angled triangles.

The Sine Rule allows us to find unknown angles and sides in a non-right-angled triangle. It relates angles and sides together as a ratio.

We can label a non right-angled triangle like this

Angles correspond with the sides opposite them, and are labelled with the same letter. We use capital letters for the angle, and lower case for the side to prevent confusion.

In non-right-angled triangles, angles correspond with which sides?

Using a triangle labelled in this way, we can use the Sine Rule to find unknown angles and sides.

The Sine Rule relates angles and sides as a ratio

Opposite angles and sides (labelled with the same letter) each exist in a ratio with one another. Substituting values into this equation allows us to find unknown quantities.

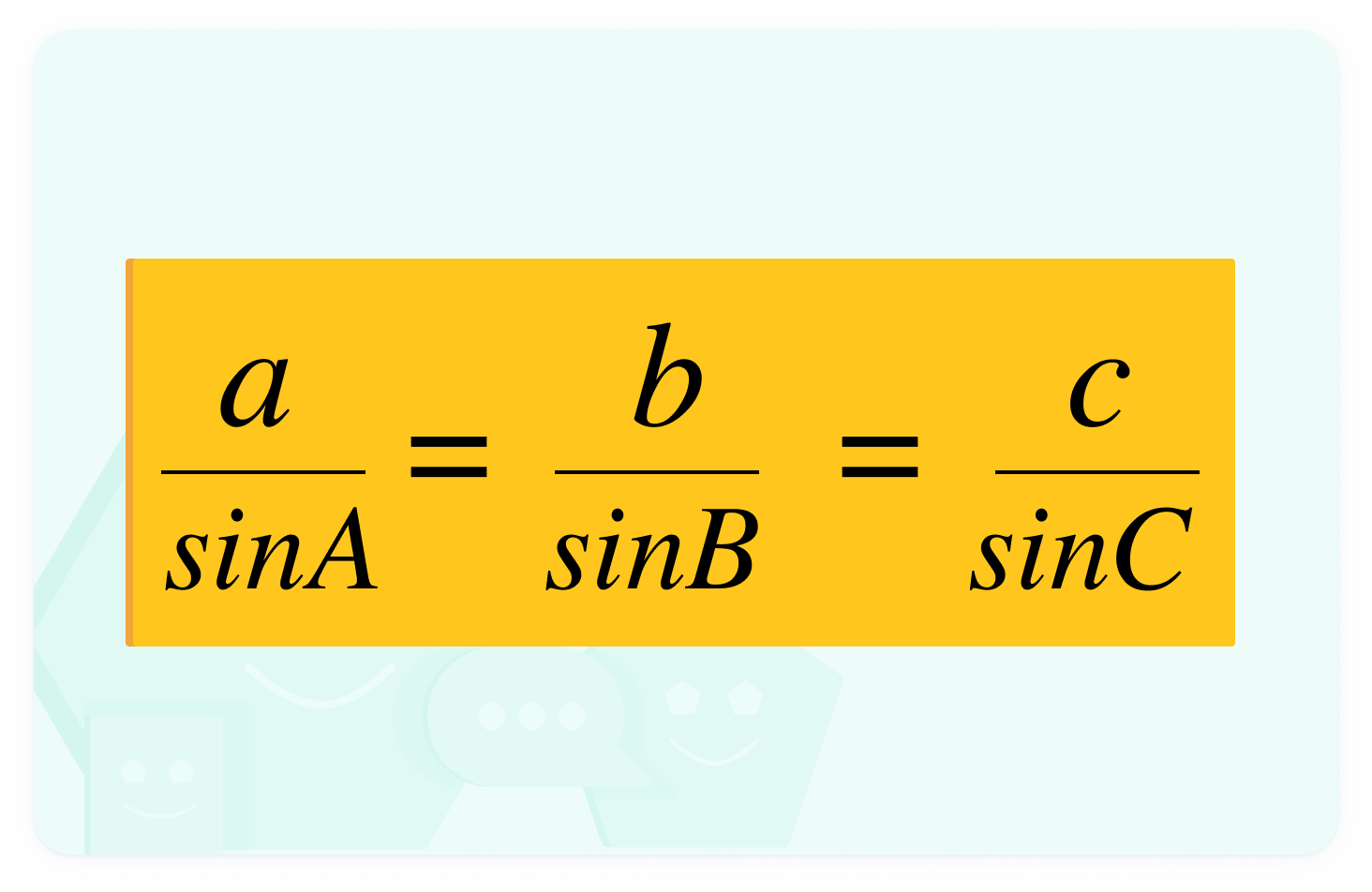
In practice, we only need to use two of these fractions

Usually, we will have 3 known values, which we can subsitute in to find a single unknown value. Since the ratios are all equal, the two we need depends on the problem we need to solve.

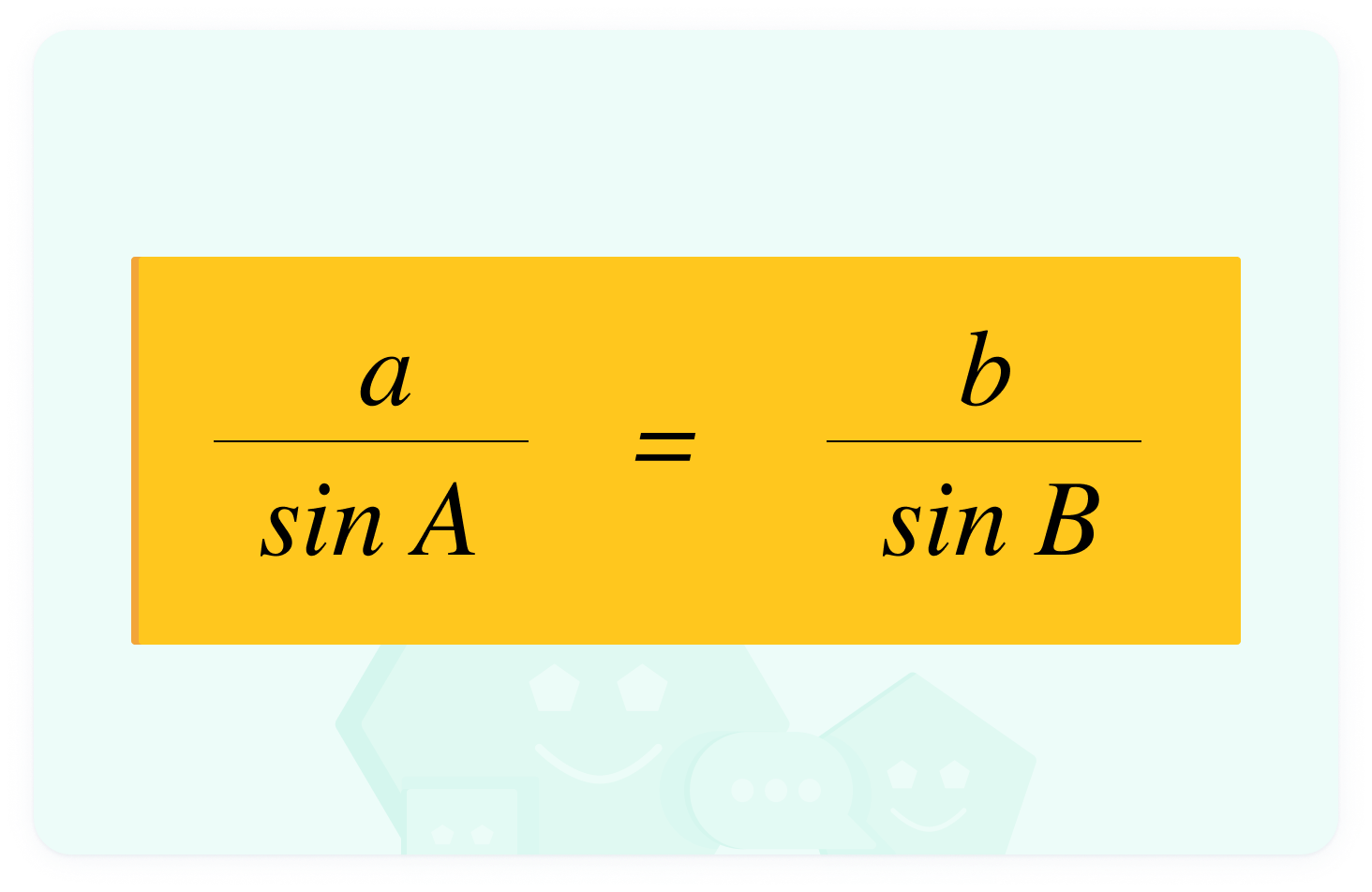
We can also find angles using the Sine Rule, if we are initially given two sides and an angle. To make this easier, we can use a slight variation on the Sine Rule we have already seen.

This is the Sine Rule we have just seen

This version is best for finding sides, as the unknown side is on top of the fraction. Therefore, rearranging the equation is simpler.

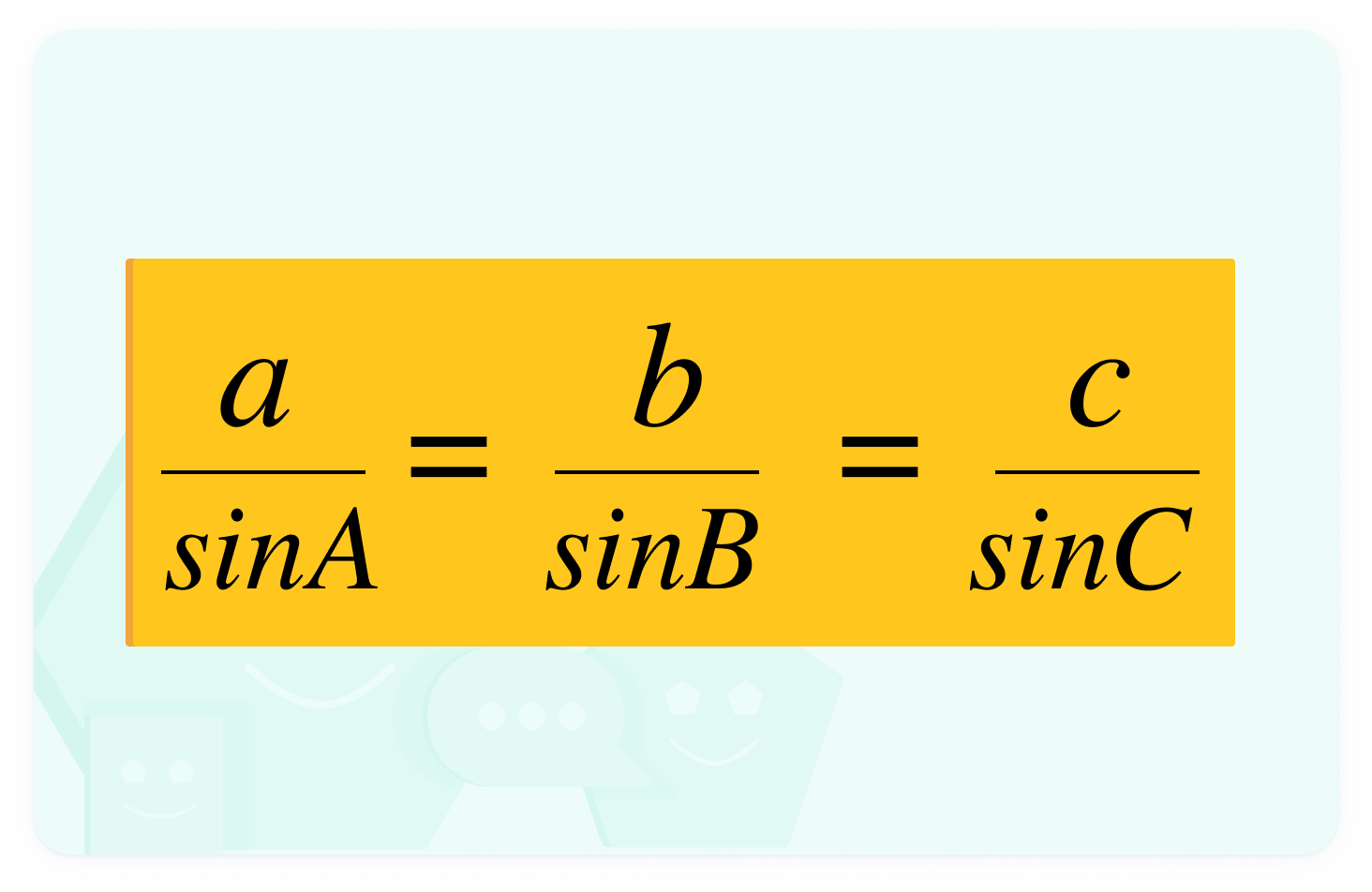
When finding angles, use this version

In this version, the unknown angle is on top of the fraction, so rearranging the formula is simpler.

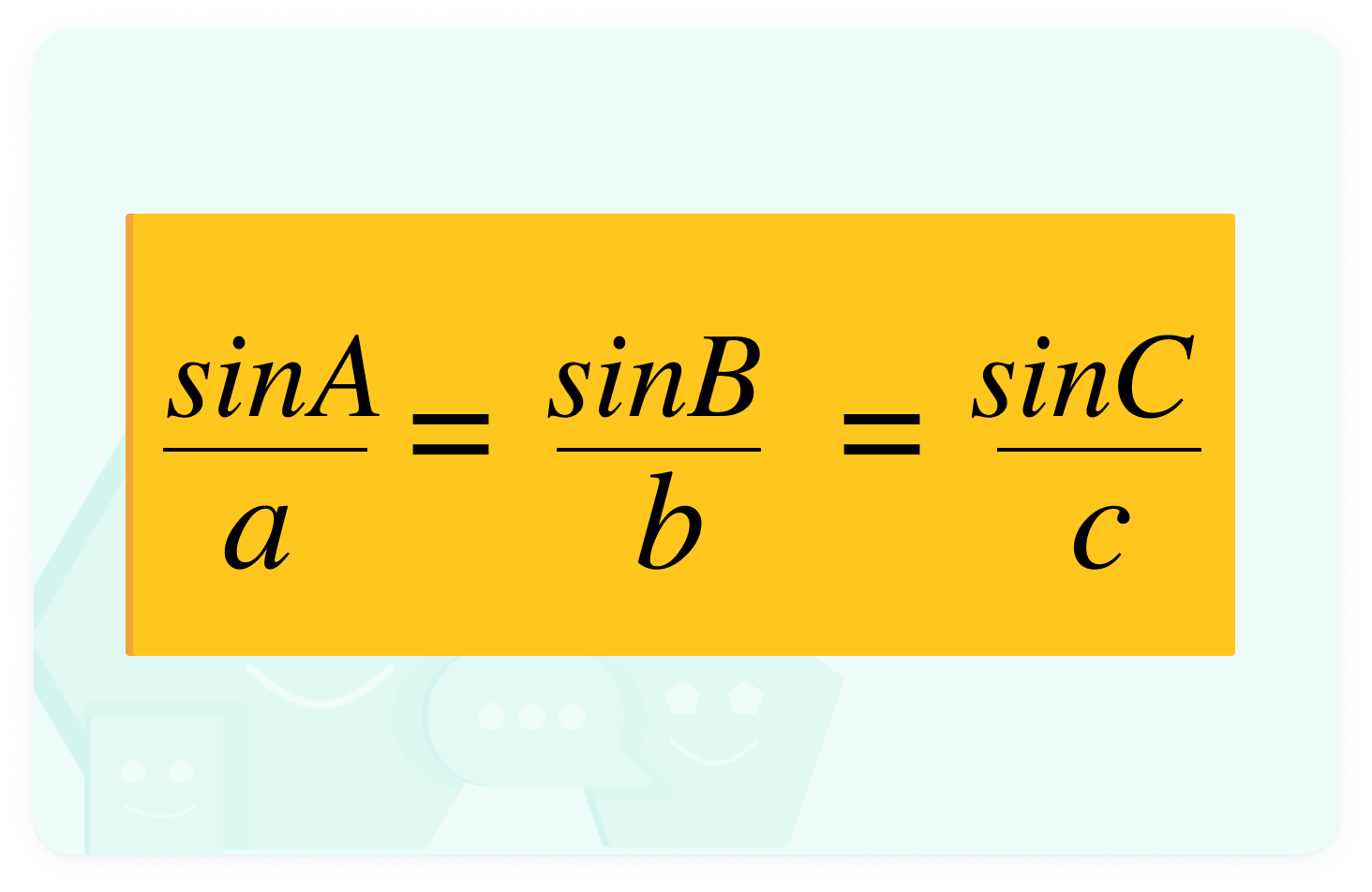
If you work out values like $sin(47.8\degree)$ in stages, make sure you maintain the accuracy of those values to several more significant figures that needed for the ultimate answer.