Geometry

YOU ARE LEARNING:

Trigonometry Ratios & SOHCAHTOA

We can use ratios between sides in a right-angled triangle to find angles within them. These ratios are called trigonometric ratios.

The sine, cosine and tangent functions appear in many branches of mathematics and science. They come from geometry, and represent ratios of side lengths in right-angled triangles.

In a right-angled triangle, the hypotenuse (hyp) is always the longest side.

Relative to a given angle, the other two sides of a right-angled triangle have special names. The adjacent (adj) side is the one that touches the angle x, whereas the opposite (opp) side does not.

These are the named sides of a right-angled triangle

Notice that the hypotenuse is the longest, the adjacent touches angle $x$ , and the opposite does not.

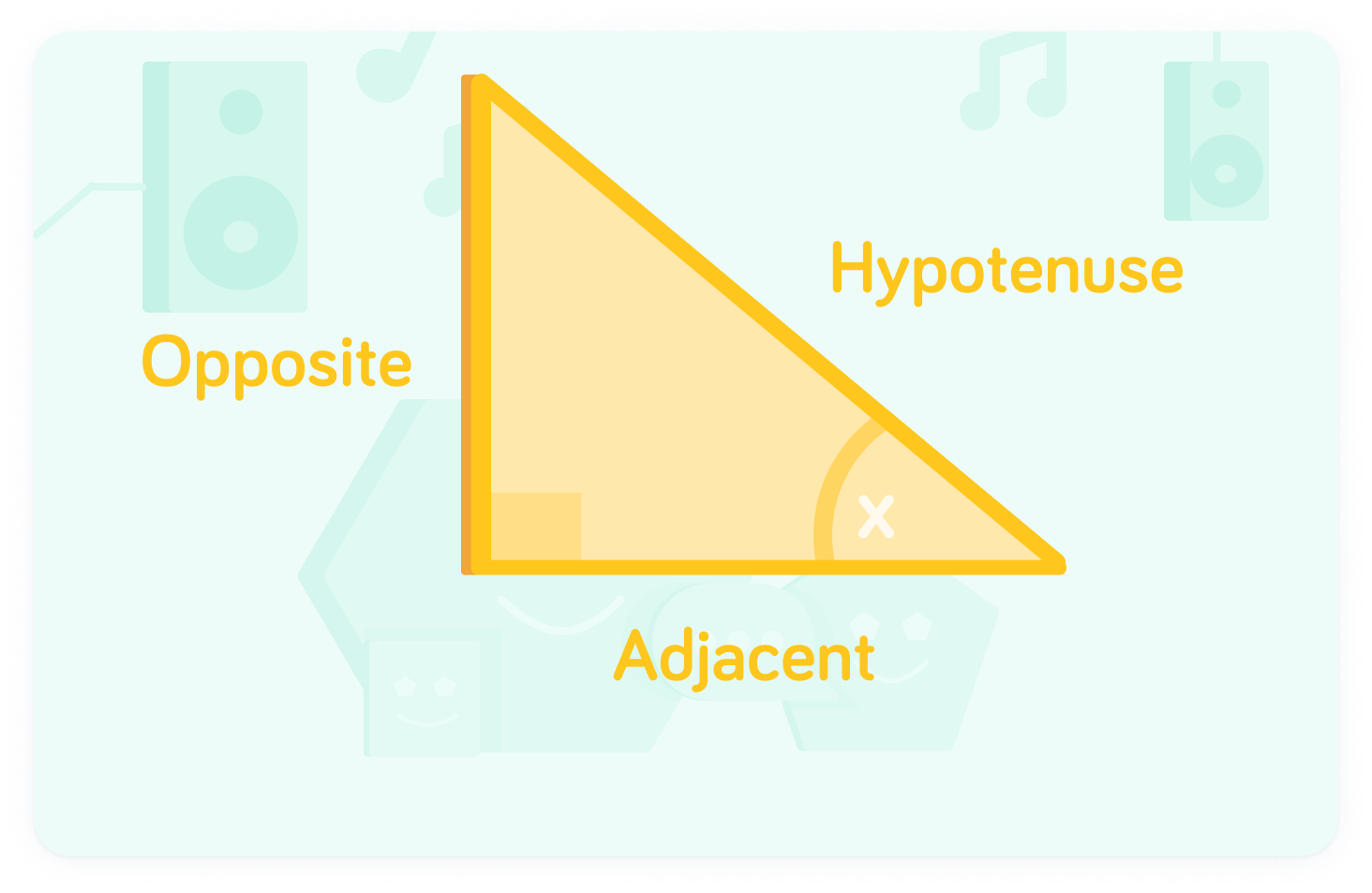
Which of these options best describes the adjacent side?

We are able to use the Sine, Cosine and Tangent functions to find the length of one of the sides, given the angle and the length of another side. Sine, Cosine and Tangent are often shortened to sin, cos and tan respectively.

For an angle $x$ :

$sinx = \frac{opp}{hyp}$ , $cosx =\frac{adj}{hyp}$ and $tanx=\frac{opp}{adj}$

We can remember these ratios using SOHCAHTOA

The letters correspond to the order of the items in each ratio. For example, the Sine ratio is $\dfrac{opp}{hyp}$ , so taking the first letter of each of the items in the equation gives us SOH

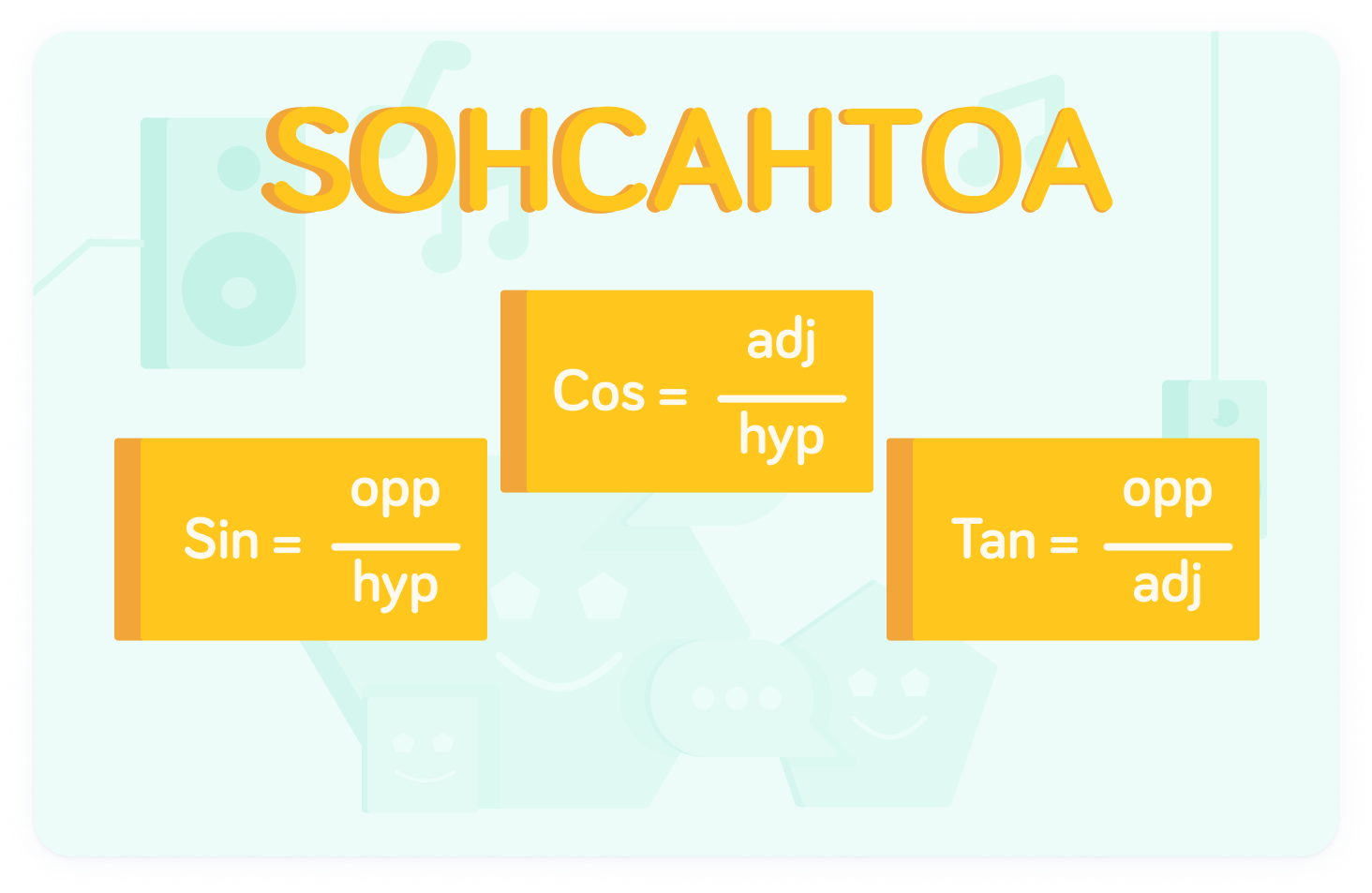
We can use these ratios to find unknown angles or sides in a right-angled triangle.

N.B. You'll need a calculator to use these three functions

The Tangent ratio is...

In the previous question, we had to multiply $cos(23) \times 12$ . You must be careful here, because $12\times cos(23)$ is not necessarily the same as $cos(23)\times 12$ .

Your calculator might think that when you enter $cos(23) \times 12$ you are asking it for $cos(23 \times 12)=cos(286)$ . This is completely different from $12\times cos23$ . We can see their values below:

$cos286 = 0.276$ (to 3 significant figures)

$12\times cos23=11.0$ (to 3 significant figures)

In general, if you are multiplying a trigonometric function by a number, write the multiplier first and the function second, like this:

$12\times cos23$