Number

YOU ARE LEARNING:

Compound Units

When we multiply and divide different units of measurement, we use compound units to describe the resulting quantities.

Compound units are quantities that are a combination of different units, and are found when we multiply and divide measurements together.

Speed is a good example of this. Depending on where you are in the world, you will use either miles per hour (mph) or kilometres per hour (kph).

If you are travelling at 60mph, this means that for every hour of travel, you will travel 60 miles.

The units come from the formula for speed which is $\dfrac{distance}{time}$ . Therefore, when we say miles per hour, we are really thinking of $\dfrac{miles}{hour}$

A car travels at a constant speed for 90km. The journey takes 1.5 hours. What is its speed?

Sometimes, you may find speed recorded in metres per second. In this case, it is conventional to give the units as $ms^{-1}$ . Remember that a negative power indicates a reciprocal, so this is the same as $\dfrac{m}{s}$ or metres per second.

A sprinter runs the 100m in exactly 10 seconds. What is the sprinter's average speed?

Another example of compound units is pressure, which is defined as $\dfrac{force}{area}$ . The standard units for pressure are Pascals (Pa).

1 Pascal = 1 Newton/metre $^2$ (N/m $^2$ )

What is the pressure exerted by a force of 20 Newtons acting uniformly on a table with area $0.8m^2$ ? Choose all that apply.

You can select multiple answers

You also need to be able to calculate individual quantities from compound units. You can do this by rearranging the formulae.

Here's an image showing the rearrangement of the equation

Both sides are divided by speed

A car is travelling at 70mph. How long would it take to travel 20 miles to the nearest minute?

What is the pressure exerted hammer hitting a nail with force $8N$ on a nail head of area $0.0001m^2$ ?

You can see the equation being rearranged for volume, density and mass.

Both sides are divided by density

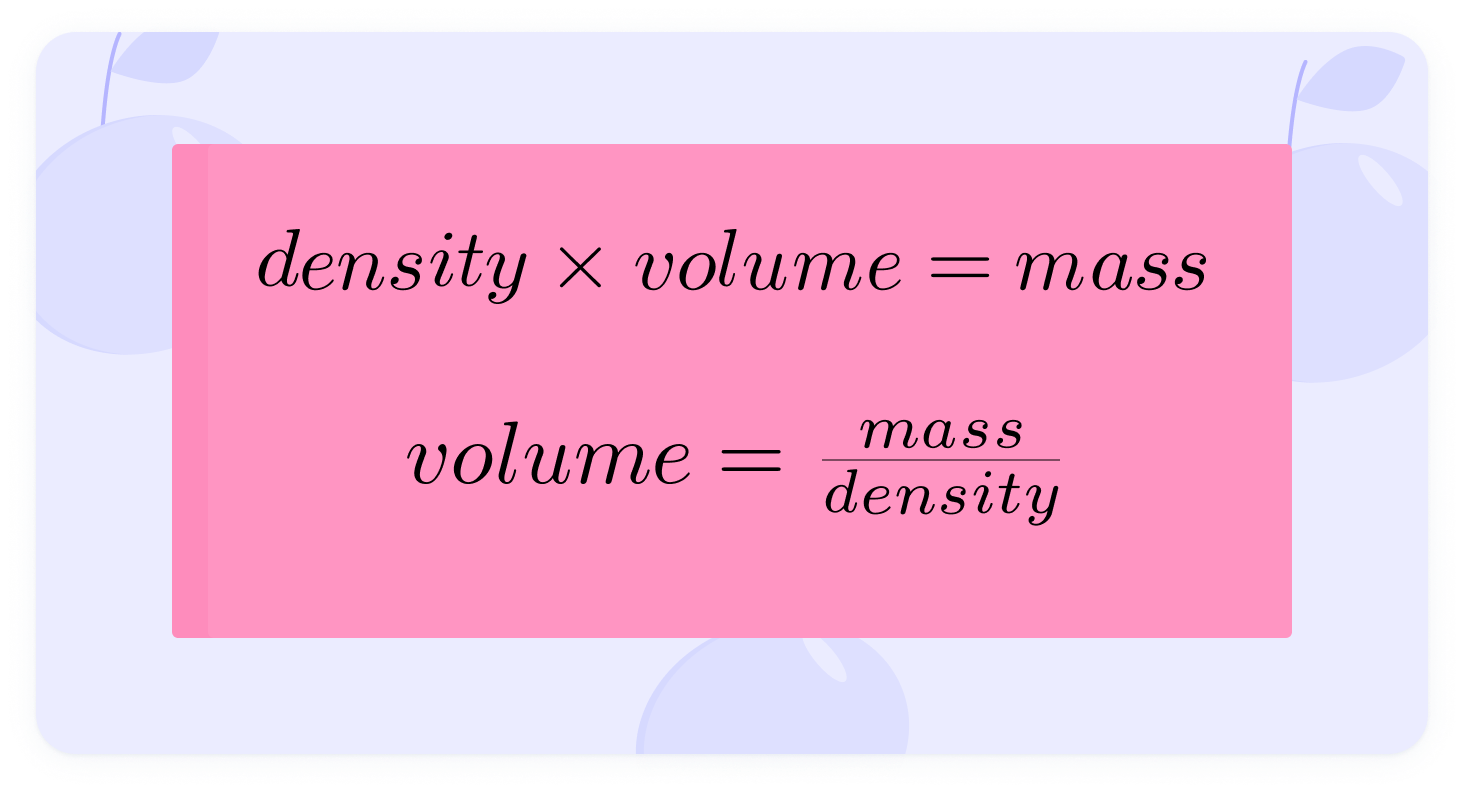
Tin has a density of $7280\space kg/m^3$ . What volume can be made from $50kg$ ?