Converting Area and Volume Units

We use units with indices to measure area and volume as there are extra dimensions which we need to account for.

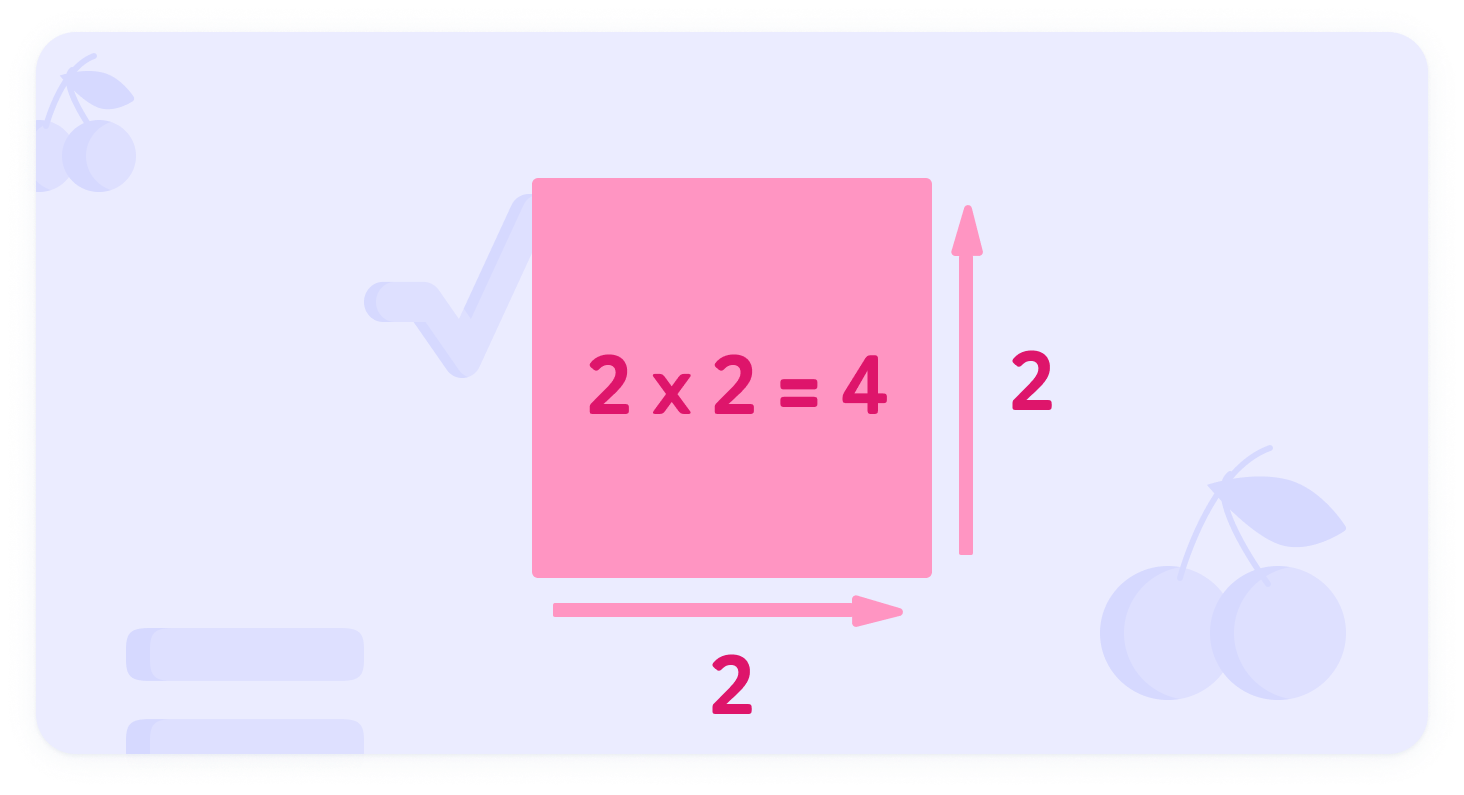
Remember that area of a square is calculated by multiplying the length of two sides together.

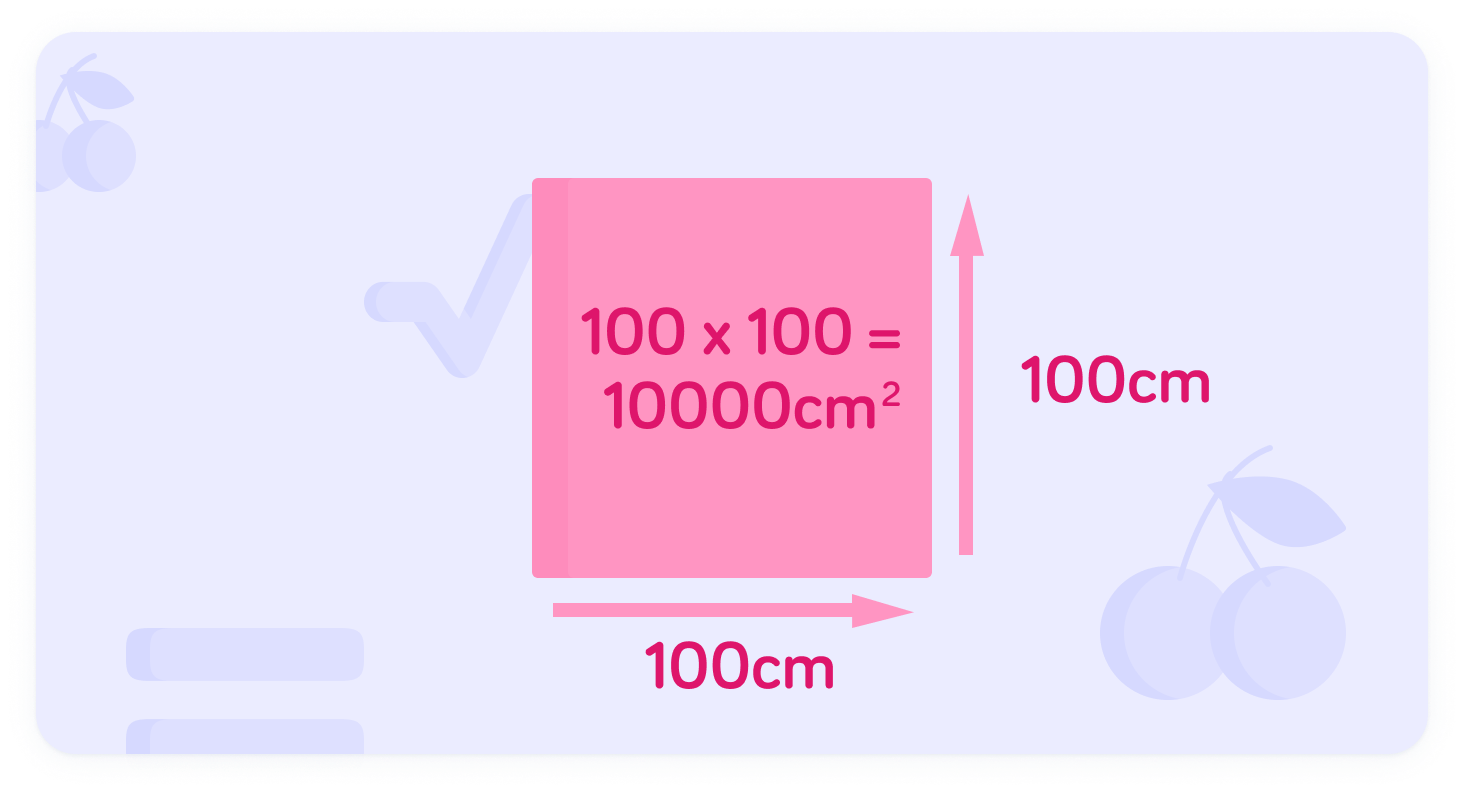
When we record area, it is given in square units. This is because we need to account for the length and height dimensions. Often we use square centimetres -$cm^2$- or square metres -$m^2$. But how many square centimetres are in a square metre?

As there are 100cm in 1m, it can be easy to think there are $100cm^2$ in $1 m^2$; but this isn't correct. A square metre is:

$100cm \times 100cm = 10000cm^2 = 1m^2$

A similar approach can help us understand how many square metres in a square kilometre.

There are $1000m$ in a kilometre.

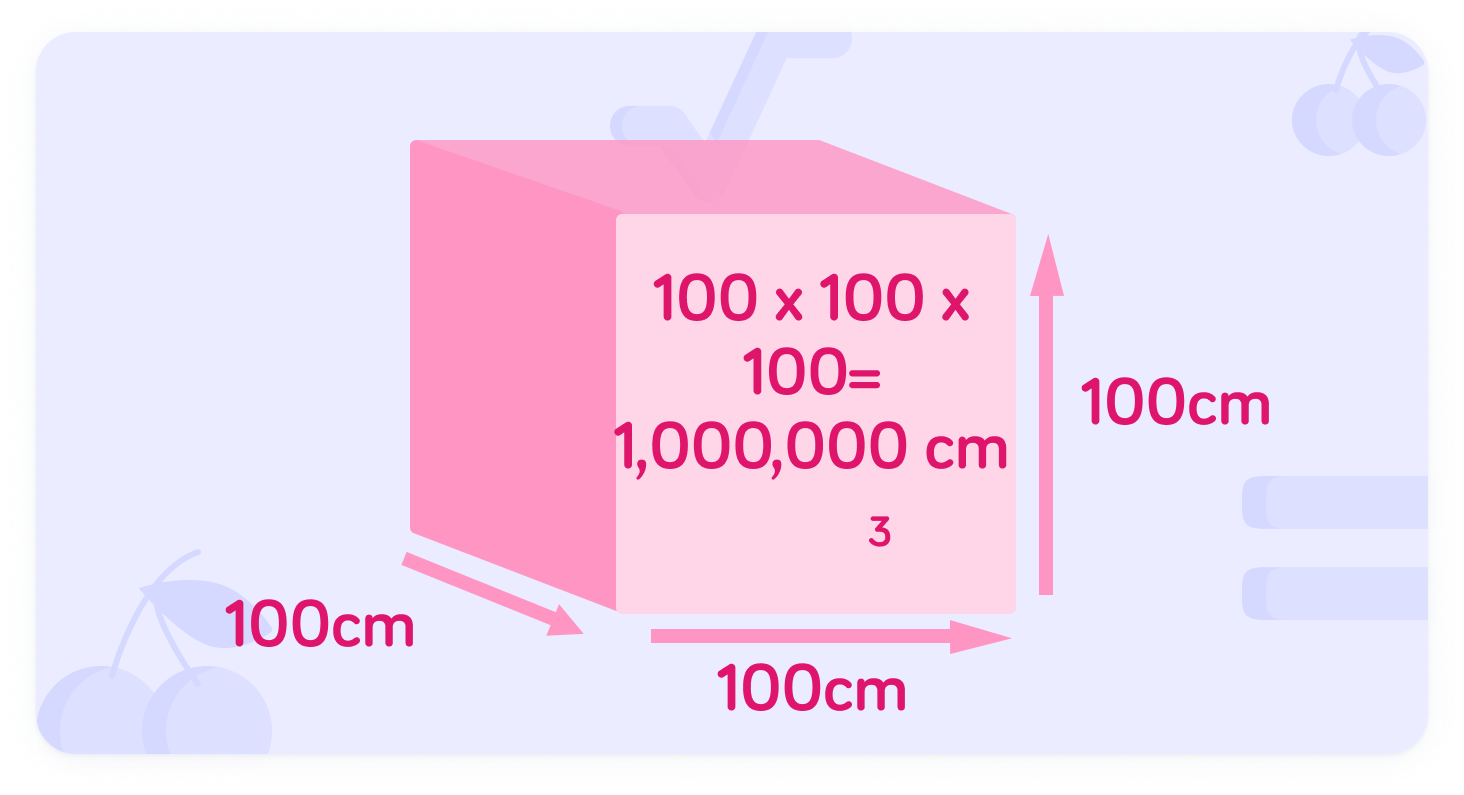
Volume is measured in cubic units, often cubic centimetres - $cm^3$ - or cubic metres - $m^3$.

If we consider a $1m^3$ cube we can calculate how many $cm^3$ in $1m^3$.

Similarly: $100mm^2 = 1cm^2$

$1000mm^3 = 1cm^3$

You may also have to work with a unit of area called hectares.

1 hectare (ha) = $10000m^2$