Number

YOU ARE LEARNING:

Decimals and Place Values

Decimals and Place Values

Decimals are another way to represent numbers which are not whole. They also have place values.

This is a number line

In-between the whole numbers (the integers), there are numbers slotted in that are not whole.

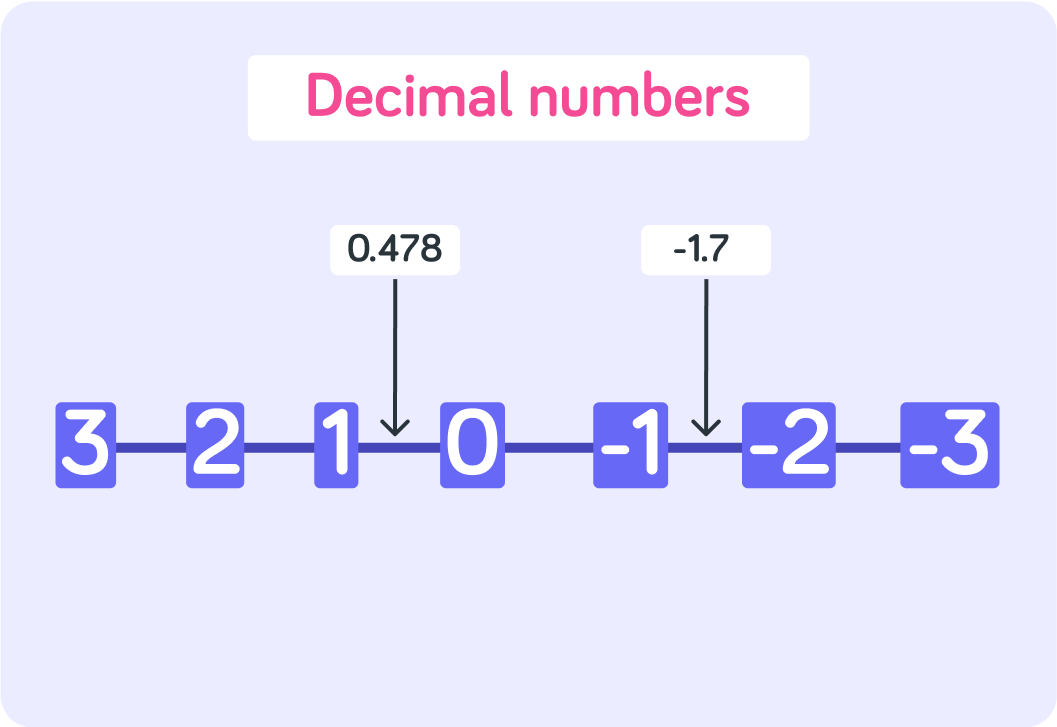
These numbers that are not whole numbers are called _________ numbers.

So what do you think you call the "dot" in decimal numbers?

A) Number point B) Decimal point

So decimal numbers are numbers in-between whole numbers

This lesson focuses on how much the ciphers after the decimal point are actually worth.

For example, how much is the $7$ worth in $0.478$ ?

First of all, though!

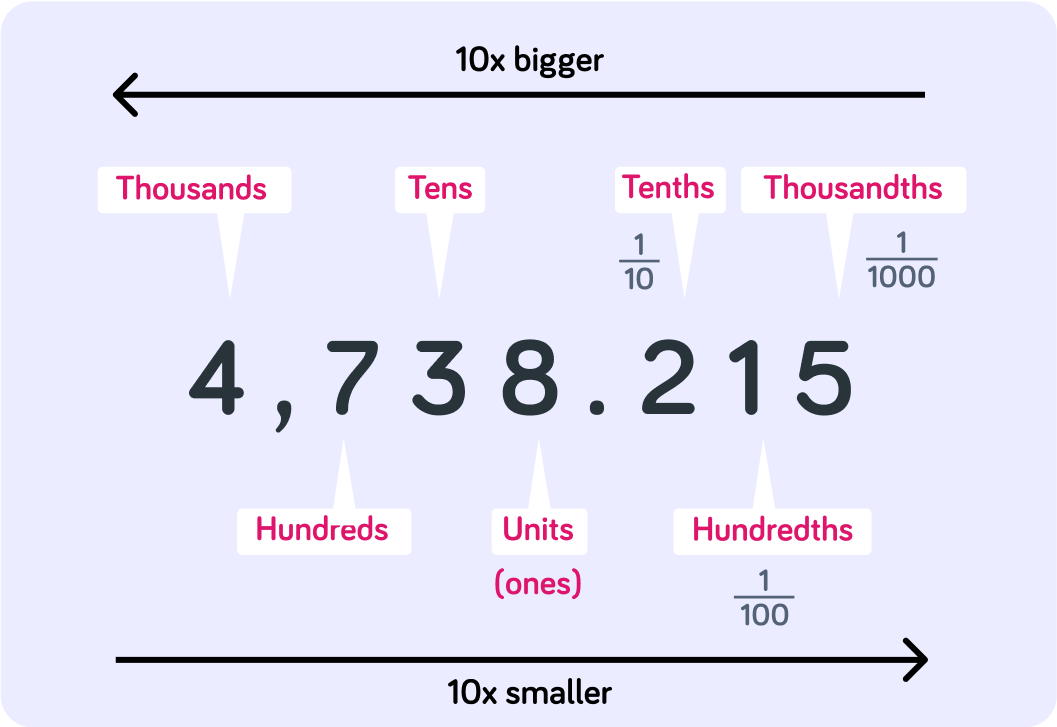
Have a look at the place values of the numbers before the decimal point.

What is the place value of the $4$ in this example?

A) $1,000$ B) $100$ C) $10$

How much is the $4$ "worth" then?

What is the place value of the $7$ ?

A) $1$ B) $10$ C) $100$

True or false? Every time you move one place value to the left, the place value gets $100\times$ larger.

Every time you move one place value to the left, the value gets $10 \times$ larger

Tens are $10\times$ larger than units. Hundreds are $10\times$ larger than tens. Thousands are $10\times$ larger than hundreds.

Now, how about the place value of the decimals?

Decimals are the numbers after the decimal point.

True or false? The $5$ in this number has place value $1,000$ just like the $4$ ?

The $5$ has place value $\frac{1}{1,000}$ or "one thousandth"

The $4$ on the left-hand-side of the decimal point has place value thousand, so it is worth $4,000$

The $5$ on the right-hand-side of the decimal point has place value thousandth, so it is only worth $0.005$

Is the place value for the $1$ bigger or smaller than the place value for the $5$ ?

A) Bigger B) Smaller

What place value does the $1$ have?

A) $\frac{1}{10}$ B) $\frac{1}{100}$

What is the place value for the $2$ ?

Every time you move one place value to the right, the place value gets $10\times$ ___________.

A) larger B) smaller

So the place values are smaller than $1$ on the right-hand-side of the decimal point

1 tenth is the same as $\frac{1}{10}$ 1 hundredth is the same as $\frac{1}{100}$ 1 thousandth is the same as $\frac{1}{1,000}$

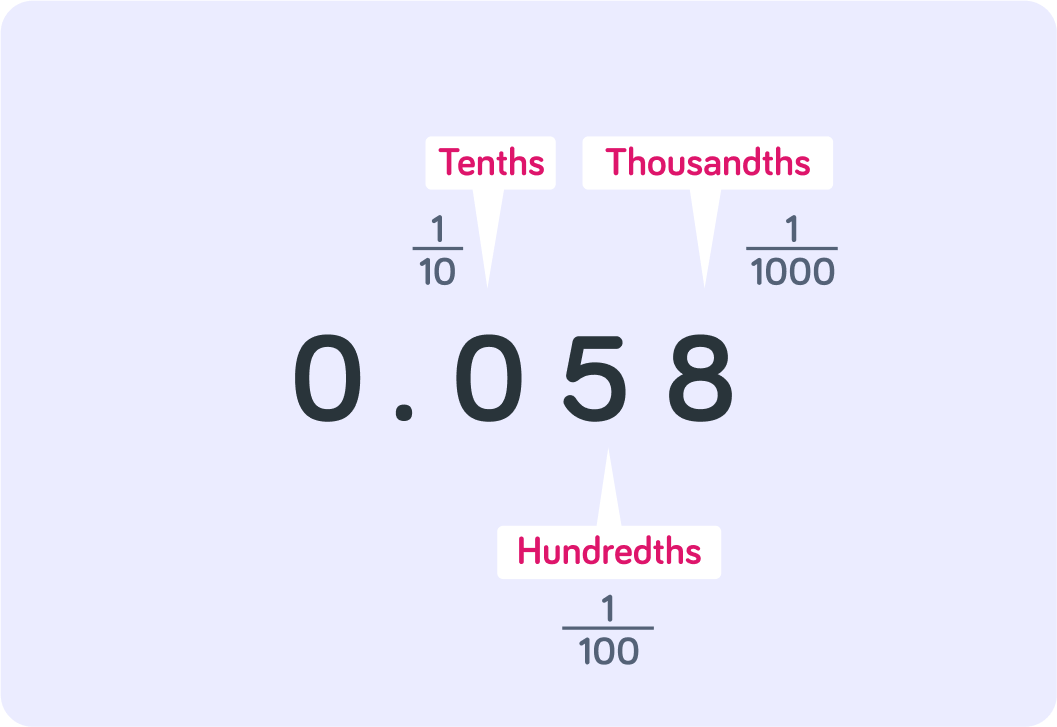
How many tenths are there in this decimal number?

How many hundredths are there in this decimal number?

How many thousandths are there in this decimal number?

So $0.472$ has...

4 tenths. 47 hundredths. 472 thousandths.

How many hundredths are there in the decimal number $0.025$ ?

How many tenths are in the decimal number $0.379$ ?

How do you write 34 hundredths as a decimal number?

How do you write 583 thousandths as a decimal number?

Now! How do you write 23 thousandths as a decimal number?

Which one is the biggest decimal number?

Summary! Decimal numbers are numbers in-between whole numbers

Decimals are the numbers that follow the decimal point.

Decimals have place values

The first decimal has place value $\frac{1}{10}$ (1 tenth). The second decimal has place value $\frac{1}{100}$ (1 hundredth). The third decimal has place value $\frac{1}{1,000}$ (1 thousandth).

Place values change by $10\times$ when you move left or right

They get $10 \times$ bigger every time you move one place left. They get $10 \times$ smaller every time you move one place right.