Basic Concepts in Physics

YOU ARE LEARNING:

Using the Speed Formula

Using the Speed Formula

You can also use the speed formula to find time and distance.

In this lesson, we'll be practicing using the equation for speed. But first, what do we need to work out the speed of an object?

You can select multiple answers

Can you recall the equation for speed?

This runner ran $400 \space m$ in $50 \space s$ . How fast was he going in $m/s$ ?

Calculating the distance travelled

A car travels at 70 miles per hour. How many miles will it have travelled after 3 hours?

How do you rearrange $speed = \frac{distance}{time}$ to make distance the subject?

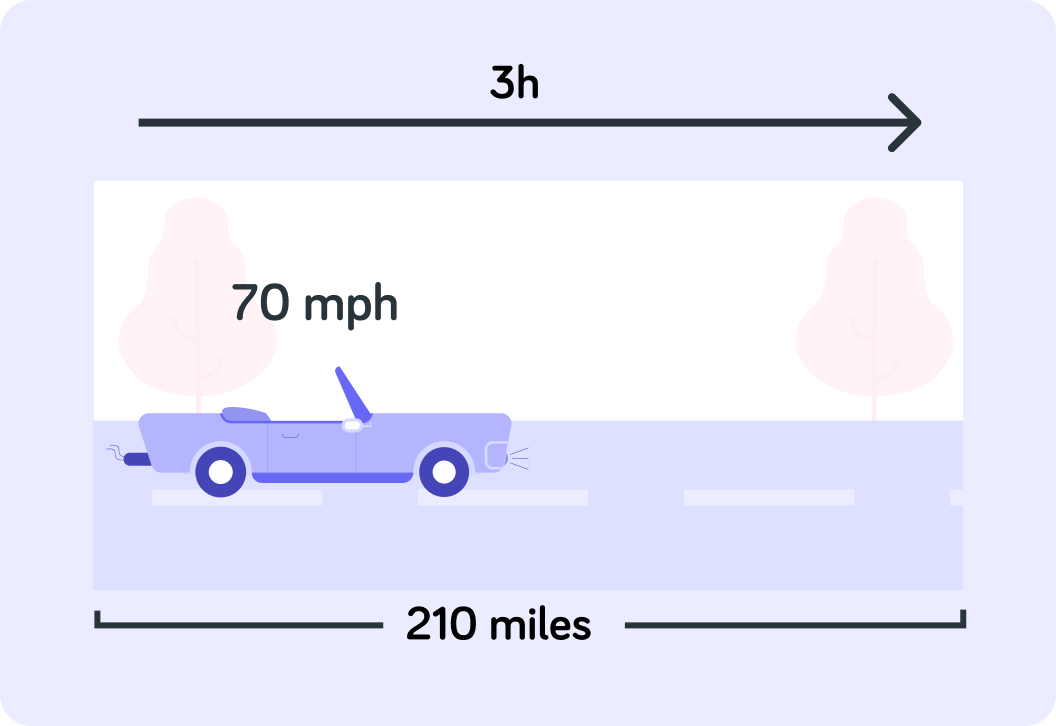
So you can rearrange the speed formula $speed = \frac{distance}{time}$

If you have the time and the speed, but need to calculate the distance you can do like this $distance = speed \times time$

Calculating the time taken

A person walks at $2 \space mph$ . How many hours will it take that person to walk $20 \:miles$ ?

So the person walked for $20\:miles$ in $10\:h$ . How have you rearranged the speed formula to make time the subject?

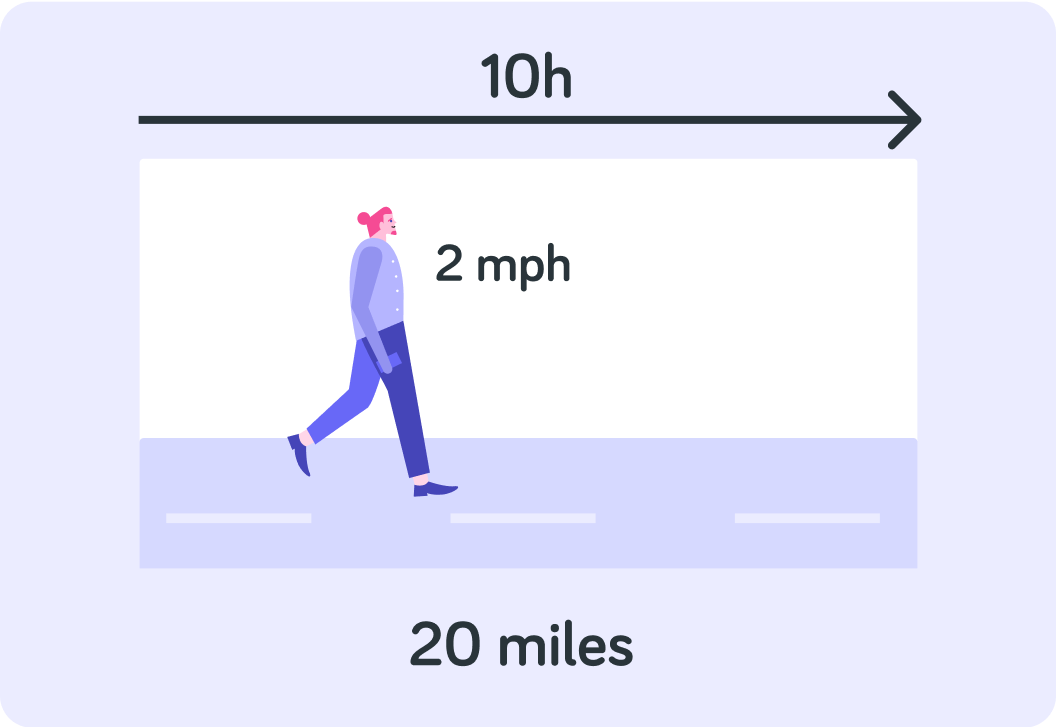
So you can rearrange the speed formula $speed = \frac{distance}{time}$

If you have the distance and the speed, but need to calculate the time you can do like this $time = \frac{distance}{speed}$

Your bus breaks down $3$ miles from the train station. You walk at $2 \space mph$ . How many hours will it take you to walk to the train station?

If you're cycling at $10 \space m/s$ , how far (in metres) do you get in $2$ minutes?

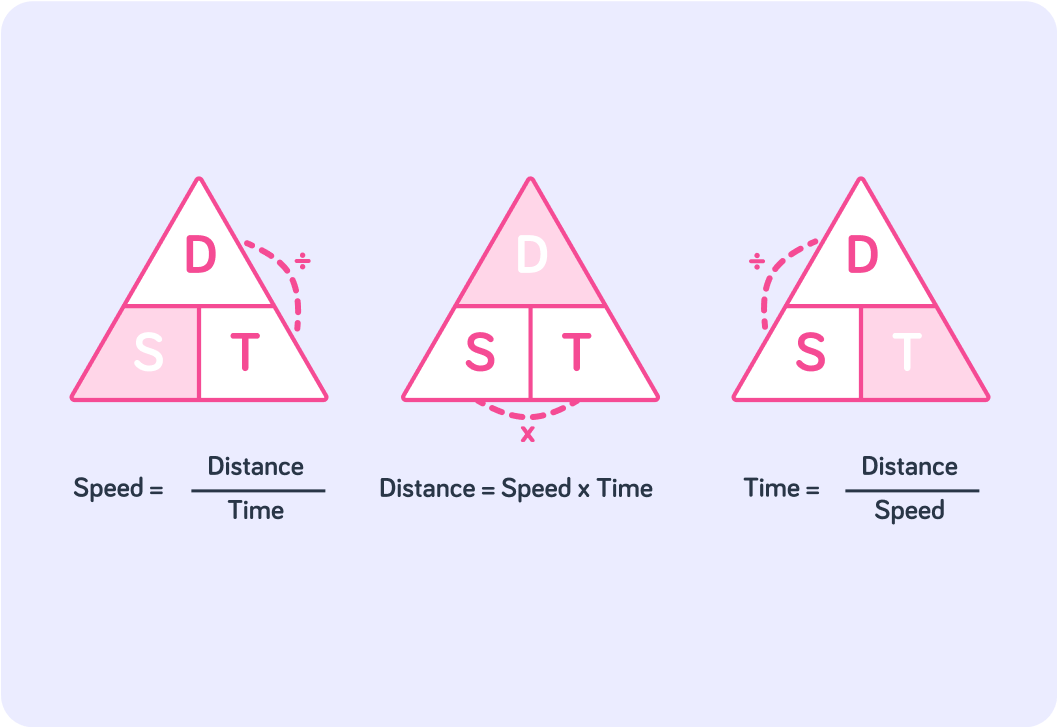
This might help you remember how you can rearrange $speed=\frac{distance}{time}$ to find time or distance

In each triangle, the darker corner is the subject of the formula. The other two either multiply if they are next to each other or become a fraction with distance on top.

Average Speed

When you travel somewhere, whether by walking or by car, do you travel at a constant speed for the whole journey?

When you calculate the speed an object is travelling over the course of a journey...

... you normally calculate the average speed **** of the object.

Does the average speed take into account changes in speed over the course of a journey? Yes or No?

So when we use the equation $speed=\frac{distance}{time}$ or any version of it...

we are using the average speed over the whole distance travelled within the time taken.

For example, Julie walks her dog in a park and stops occasionally to give him some water. In total, it takes her $2$ hours to walk $7.2\:km$ all the way around the park. What was Julie's average speed in $km/h$ ?

Summary!

You can change the formula $speed =\frac{distance}{time}$ to make either time or distance the subject

These triangles should help you remember what to divide or multiply to find speed, time or distance.

When we use these equations...

we are using the average speed over the whole distance travelled within the time taken.