YOU ARE LEARNING:
Forces at Right Angles

Forces at Right Angles
You can break down the direction of a force into its simpler component forces at right angles, that together is the same as the single force.
If a resultant force acts on a ball at an angle of 50° from the ground. Does the force have a vertical component?

A single force can be resolved into 2 component forces, acting at right angles to each other. In other words, the force is broken down into 2 forces which have the same effect as the original force.
If we resolve a single force, what do we do to it?

If we resolve a force into 2 component forces, what effect do the component forces have?

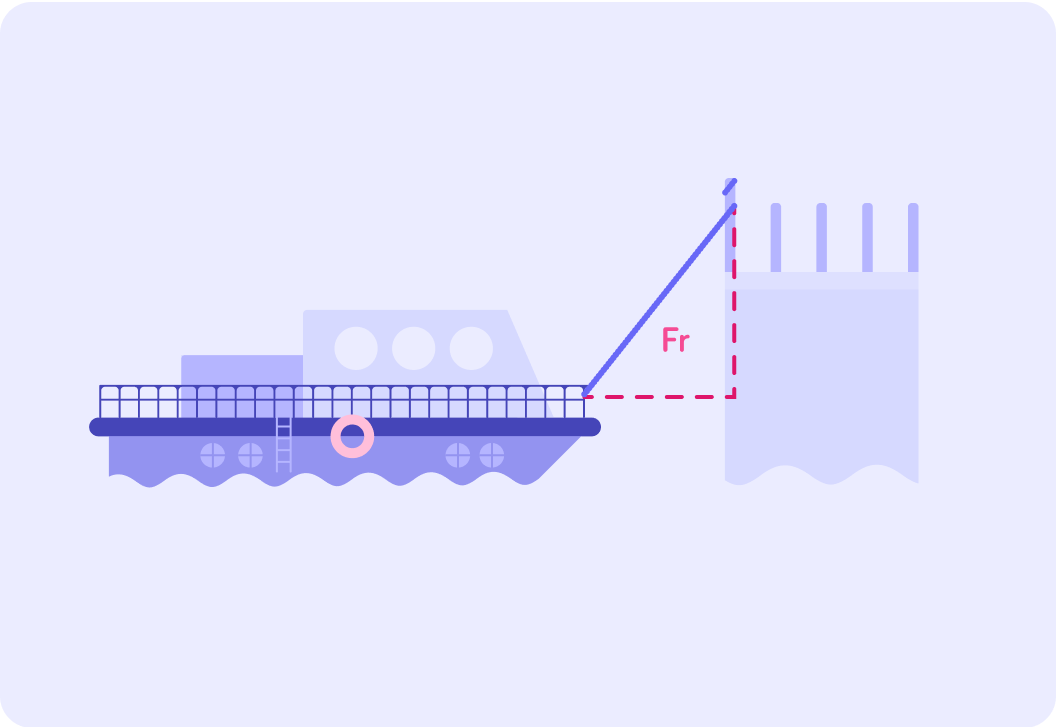
The image shows the force acting on a boat which is tied to the dock.
It acts at an angle, so there must be horizontal and vertical components to the force.
Here is the same boat with the force resolved into its horizontal and vertical components. Which two statements do you think are correct when resolving forces into 2 components?
A) Draw horizontal and vertical vectors of any length. B) Draw the horizontal and vertical vectors at right angles to each other. C) Guess the length of the vectors. D) The horizontal vector ends directly under the head of the original force.

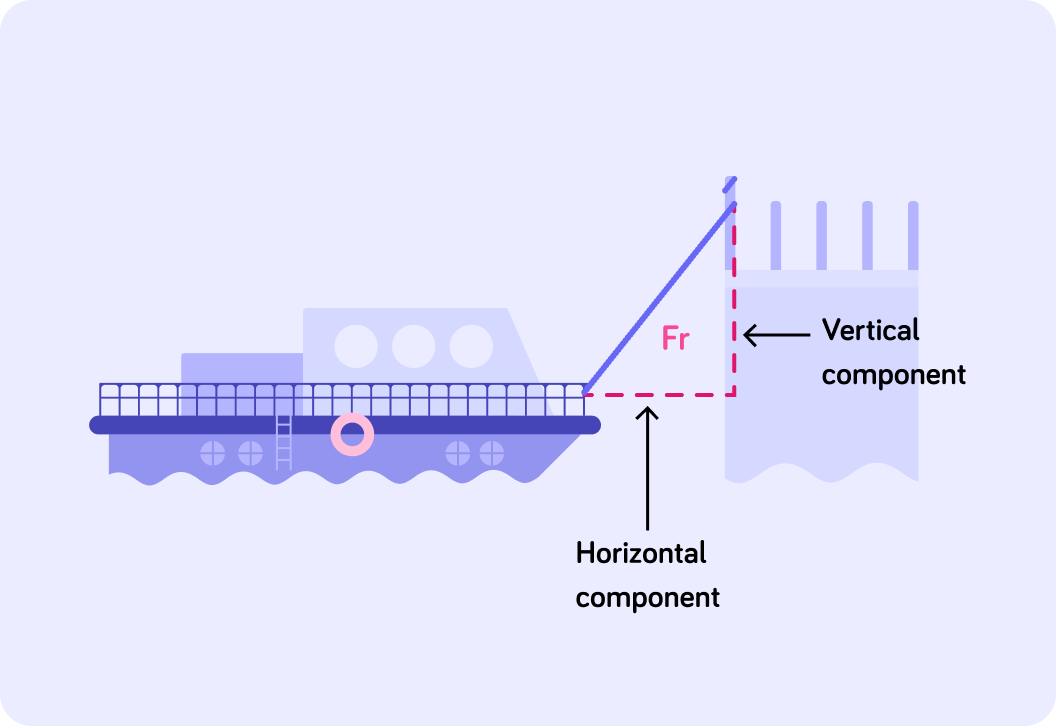
We can resolve a force and find the magnitude of the vertical and horizontal components. When we combine these components they produce a force with the same magnitude and direction as the original force. To find the magnitude of the components, we need to draw a scale diagram.
What do you notice about the triangle that forms when you resolve a force into its vertical and horizontal components?

You can select multiple answers
