Waves

YOU ARE LEARNING:

Refractive Index

The ratio of the speed of light in a vacuum to its speed in a specified medium is the refractive index of that medium.

Refraction is defined by the **** change in speed that occurs when waves pass between two media of different density.

The also causes the waves to change direction.

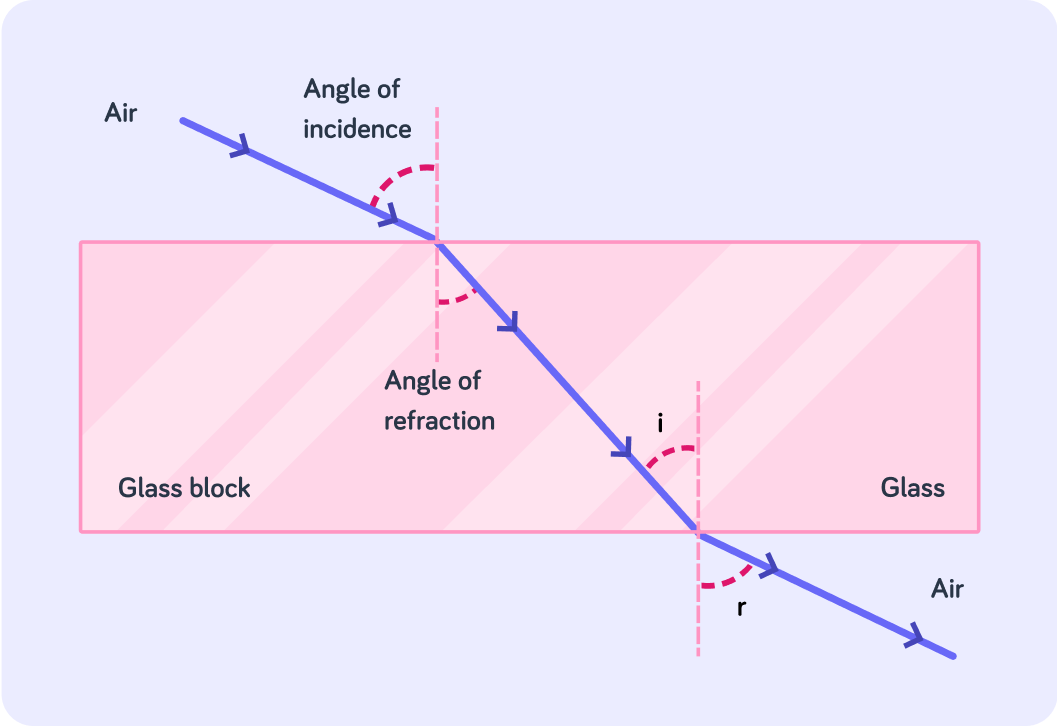
We measure this change in direction by measuring the angle of refraction This is measured between the refracted ray and the...

Consider a light ray travelling from a denser medium into a less dense medium.

Does its speed 'increase' or 'decrease'?

Does the refracted ray move 'away' or 'towards' the normal? Hint: F.A.S.T.

Is the angle of refraction going to be 'smaller' or 'larger' than the angle of incidence?

Still considering a light ray, travelling from a more dense to a less dense medium...

What is the angle of incidence called when the angle of refraction is $90^o$ ?

What do we call the phenomenon of when the angle of incidence is larger than the critical angle, $\theta_c$ ?

If the critical angle of this light ray is $30^o$ , and the angle of incidence is $45^o$ , what will the angle of reflection be?

Certain media will refract light more than others. The way we measure this is with a refractive index.

The refractive index, n, of a material is the ratio of the speed of light in a vacuum (c) and the speed at which light travels at in the material (v).

$n=\frac{c}{v}$

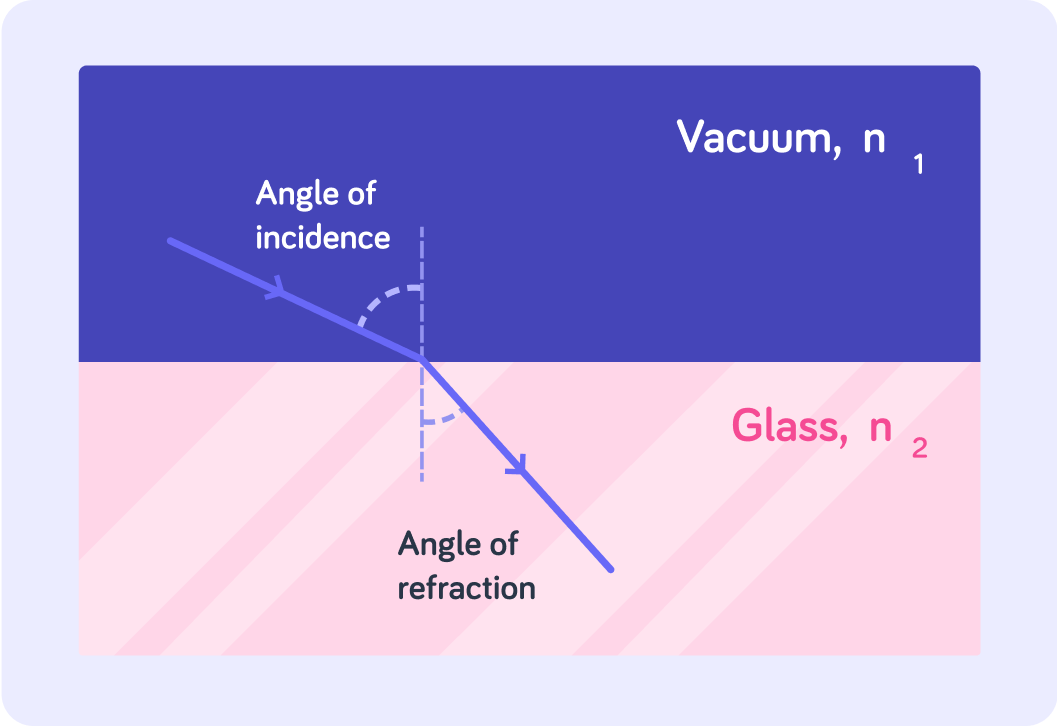
The speed of light in air is approximately $3\times10^8m/_s$ , whereas in glass it is approximately $2\times10^8m/_s$ . Calculate the refractive index n for glass.

More generally, the refractive index is the ratio of the speed of a wave in the first medium, $v_1$ , and the speed of the wave in the second medium $v_2$ .

$n=\frac{v_1}{v_2}$

The speed of light in a vacuum is $3\times10^8m/_s$ , and the speed of light in air is approximately $3\times10^8m/_s$ . What is the refractive index, n, for air?

What is the unit for the refractive index?

What would the equation for refractive index, $n=\frac{v_1}{v_2}$ , be in terms of wavelength? Use: $v=\lambda\times f$ .

What is the relationship between the frequency of light and the refractive index of a medium?

You can find the relationship of refractive index and the angles of incidence and refraction using Snell's Law.

Snell's Law relates the ratio of the refractive indices of both media with the sin of the angles of incidence and refraction as follows:

$\frac{n_1}{n_2}=\frac{sin{\theta_i}}{sin{\theta_r}}$

We've seen that the refractive index for air is 1, so when the light is travelling from the medium into air, this equation is simplified to this:

$n=\frac{sin{\theta_i}}{sin{\theta_r}}$ where n is the refractive index of the medium at the boundary with air.

The refractive index of a medium is the ratio of the speed of light in a vacuum and the speed at which it travels in the medium.
$n=\frac{c}{v}$ or more generally, $n=\frac{v_1}{v_2}$ .

Snell's Law relates the refractive index with the angles of incidence and refraction. $\frac{n_1}{n_2}=\frac{sin{\theta_i}}{sin{\theta_r}}$ The refractive index of air is 1.