Cells

YOU ARE LEARNING:

Measuring Osmosis

Measuring Osmosis

Osmosis can be measured by calculating the rate of water uptake.

Osmosis is the transport of ________ molecules in and out of cells.

In which of these cells can you measure more osmosis? Answer A or B.

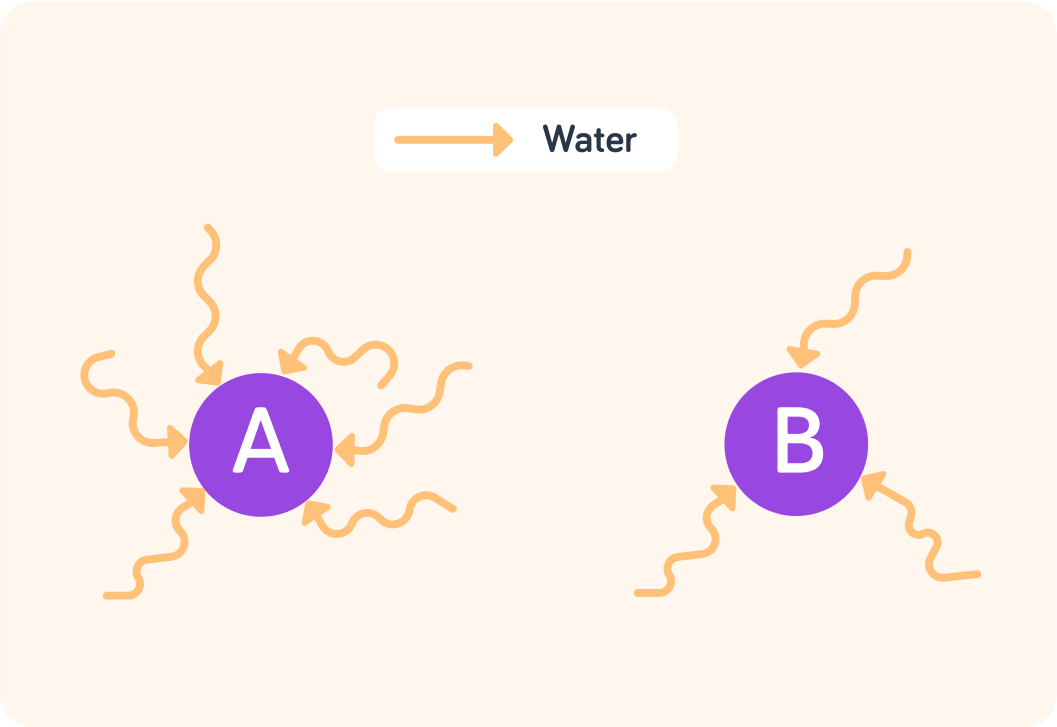
More water molecules are transported into cell A than into cell B

So we measure higher levels of osmosis in cell A than in cell B.

How do you calculate the rate of osmosis?

A wrinkled carrot weighs $50 \space g$ . After two hours in water, it weighs $55 \space g$ . How much water did the carrot take on?

So the carrot took on $5 \space g$ of water in two hours. How many grams of water did it take on per hour then?

So you calculated the transport of water like this: $\frac{55 \space g - 50 \space g}{2 \space h}=2.5 \space g/h$ . Which one is the correct formula then for calculating the rate of osmosis?

To recap! The more water molecules get transported...

the higher the levels of osmosis you will measure.

You calculate the rate of osmosis like this: $rate \space of \space osmosis =\frac{end \space mass - start \space mass}{time}$

"Rate" means you work out how much water is transported in a given time, for example per hour.

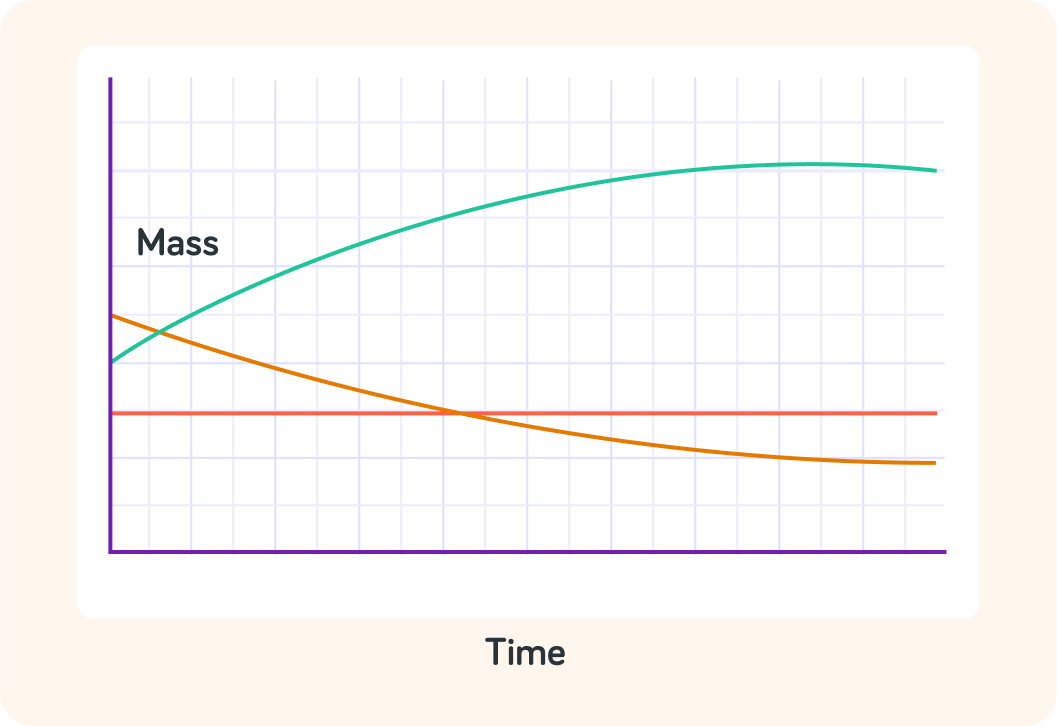
This graph shows how the mass of three apples changed over time in water

There was an orange apple, a green apple and a red apple.

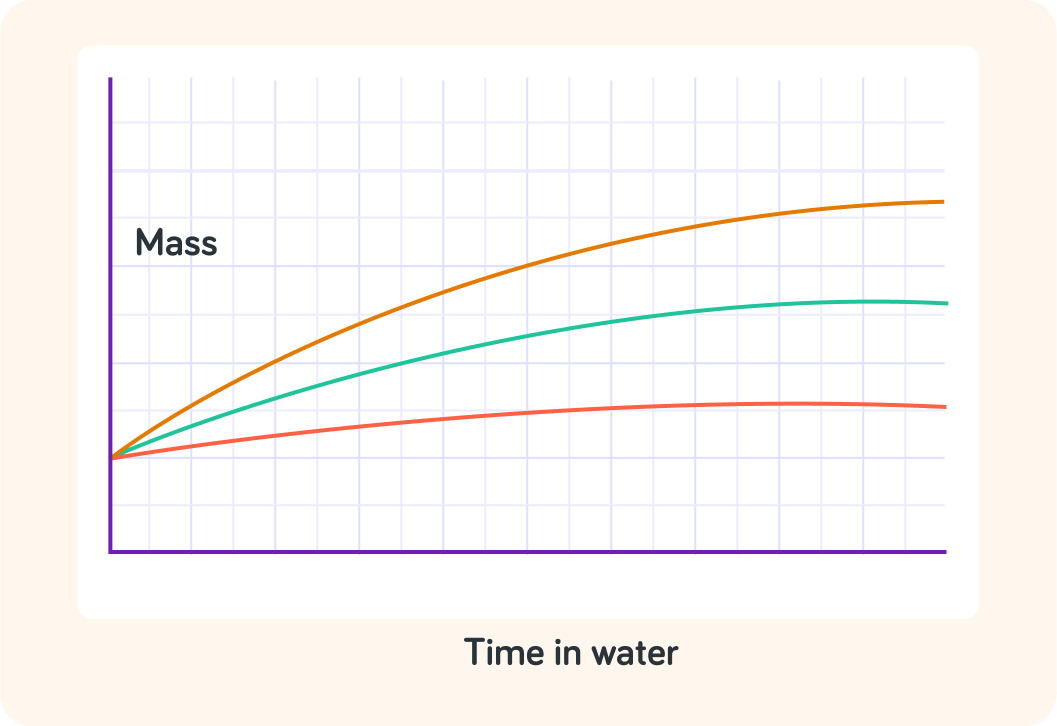
Which apple gained the most mass?

Which apple gained the least mass?

In which apple was the rate of osmosis the highest?

True or false? These three apples had the same mass before they were put in water.

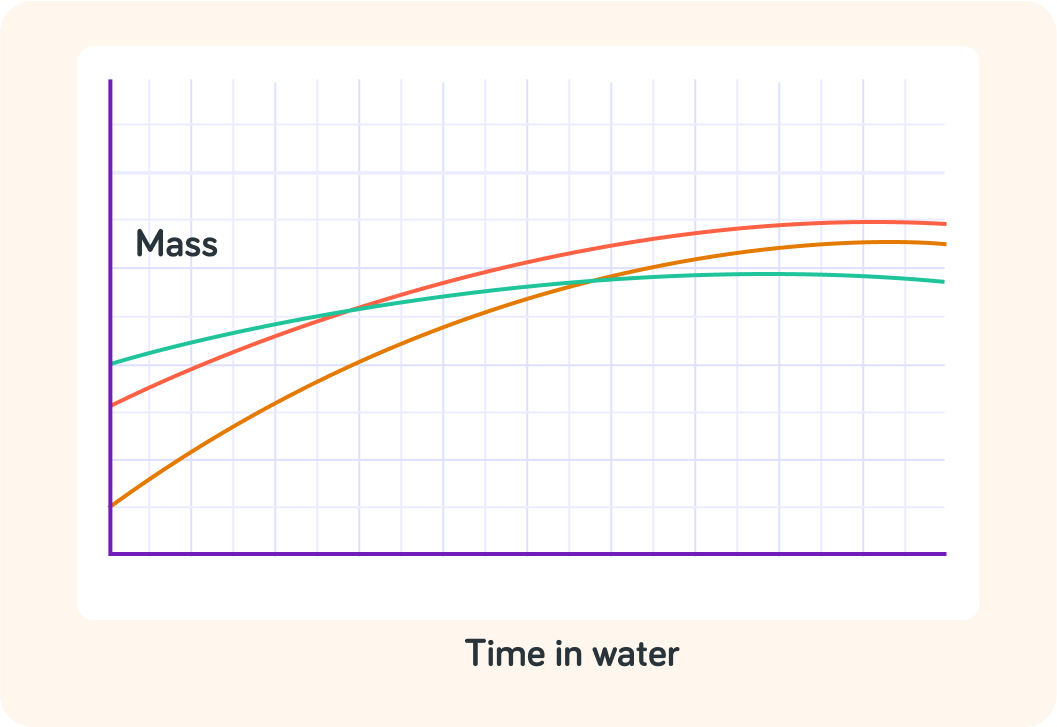
Which apple was the heaviest at the start?

True or false? The green apple was also the apple that gained the most mass while in the water?

Which apple gained the most mass while in the water?

In which apple was the rate of osmosis the highest, then?

Which direction would water molecules move in in this example?

Water molecules want to move from where there are fewer particles to where there are more

They want to dilute the concentration of particles. So in this example, they would move from left to right.

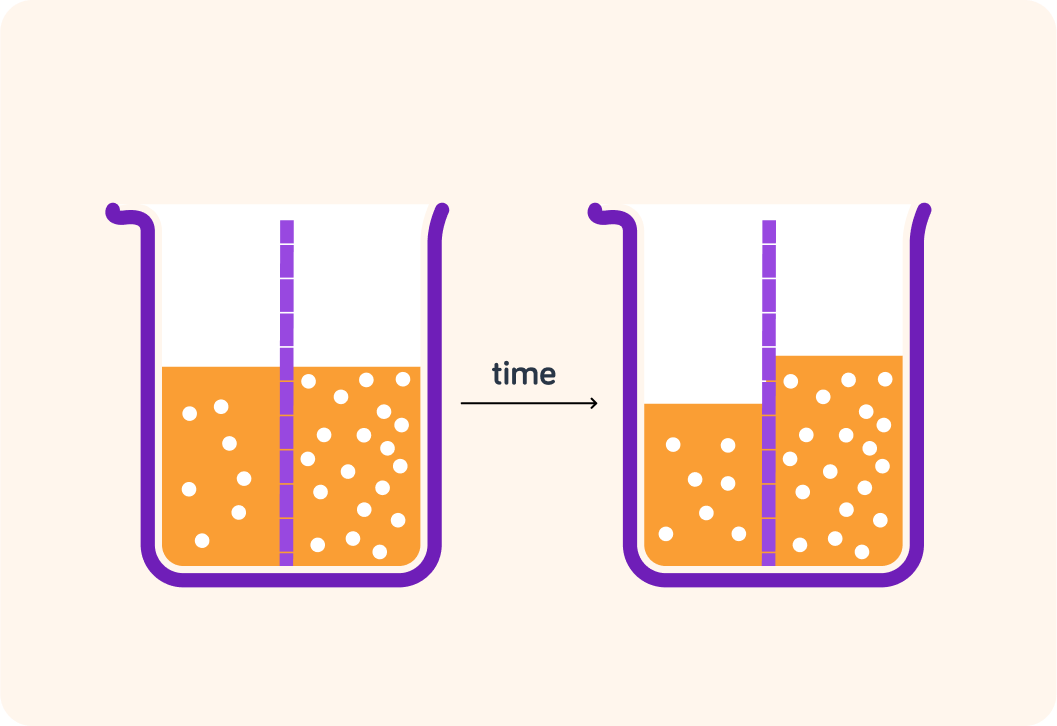
True or false? Osmosis transports water from a more dilute solution to a more concentrated solution.

These three apples have spent time in different conditions.

They have not all been submerged in the same solution.

In which apple did no osmosis take place at all?

Which apple was in a dilute solution of particles, compared to the amount of particles in the apple itself?

If there was a higher concentration of particles in the apple than in the solution...

then osmosis would make water move into the apple, so the apple's mass would increase (for example the green apple in the graph).

So which apple was in a concentrated solution of particles, compared to the amount of particles in the apple itself?

So you can read out of a graph if the object was in a dilute or in a concentrated solution

If it was in a dilute solution, its mass increased (like the green apple). If it was in a concentrated solution, its mass decreased (like the orange apple).

How do you calculate the difference in mass as a percentage?

Imagine you have another wrinkled carrot. This one weighs $100 \space g$ . After it's been in water, it weighs $103 \space g$ . How much mass did it take on?

So the carrot took on $3 \space g$ and it weighed $100 \space g$ before. You can write that as $\frac{3 \space g}{100 \space g}$ . How much is that as a percentage?

How did you turn $\frac{3}{100}$ into $3$ ?

To sum up, you worked out the percentage increase in mass like this: $\frac{103 \space g - 100 \space g}{100 \space g} \times 100 = 3\%$ . So what is the formula for calculating percentage increase in mass?

So you can calculate the percentage increase in mass like this

$\% \space mass \space increase = \frac{end \space mass - start \space mass}{start \space mass} \times 100$

What is the percentage increase in mass of a carrot that weighs $50 \space g$ before it has been in water and $55 \space g$ after it has been in water?

Summary! Osmosis is the transport of water molecules in and out of cells

Osmosis moves water molecules from a more dilute solution to where the solution is more concentrated.

You can read out of a graph if the object was in a dilute or in a concentrated solution

If it was in a dilute solution, its mass increased. If it was in a concentrated solution, its mass decreased.

You can calculate the rate of osmosis like this

$rate \space of \space osmosis =\frac{end \space mass - start \space mass}{time}$

You can calculate the percentage of mass increase like this

$\% \space mass \space increase = \frac{end \space mass - start \space mass}{start \space mass} \times 100$