Cells

YOU ARE LEARNING:

Microscopes and Magnification

Microscopes and Magnification

Magnification is the relationship between the size of the image and actual size of the object being magnified.

How big is a typical cell?

Cells are so small you can fit 10-100 of them next to each other in a millimetre! What piece of equipment do we use to see them?

Microscopes magnify things. What does that mean?

How big is the actual cell under this microscope?

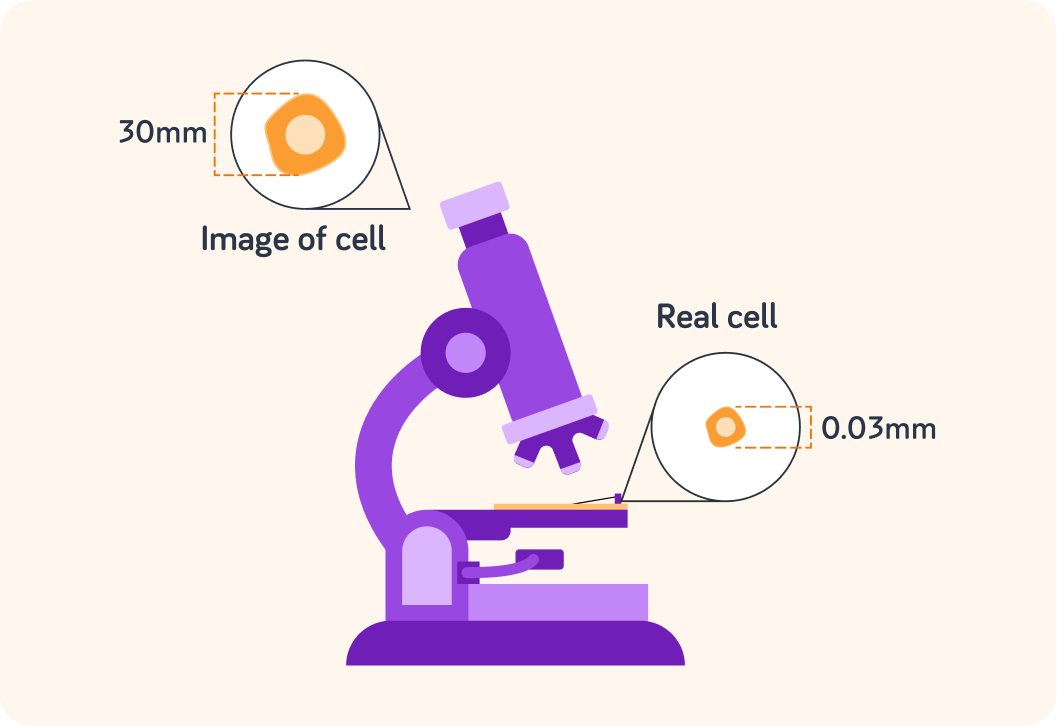
How big does the cell appear in the image you see when you look in the microscope?

So the real cell is $0.03 \space mm$ and the image of the cell is $30 \space mm$ . How many times bigger is the image than the real cell?

You worked out this microscope's magnification like this $\frac{30 \space mm}{0.03 \space mm}=1,000$ . What is the formula for working out magnification?

A) $magnification = \frac{image \space size}{real \space object \space size}$ B) $magnification = \frac{real \space object \space size}{image \space size}$

So you work out magnification like this $magnification = \frac{image \space size}{real \space object \space size}$

For example, if a cell is actually $0.03 \space mm$ big, but it appears to be $30 \space mm$ big in the microscope, then the magnification is $\times 1,000$

How big is the real cell here?

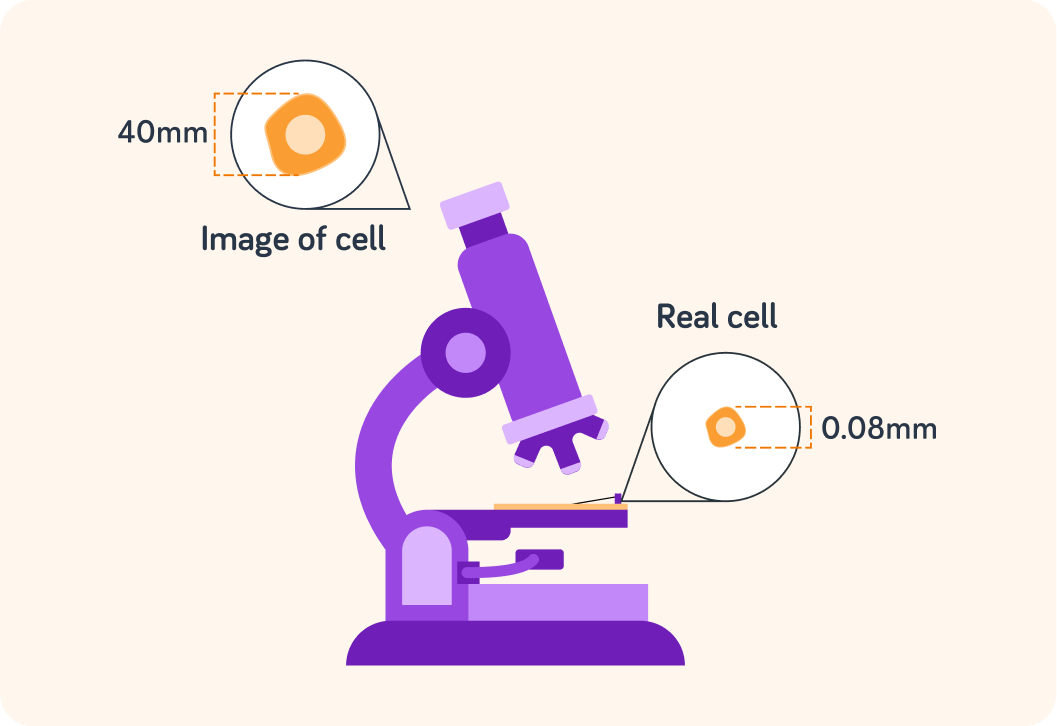
What is the size of the cell in the microscope image?

Use $magnification = \frac{image \space size}{real \space object \space size}$ to work out the magnification here.

In this case the image is 500 times bigger than the real cell

The image size is $40 \space mm$ and the real cell is $0.08 \space mm$ , so $magnification = \frac{40 \space mm}{0.08 \space mm}=500$

What unit is the size of the cell given in here?

A) Millimetres B) Micrometres C) Nanometres

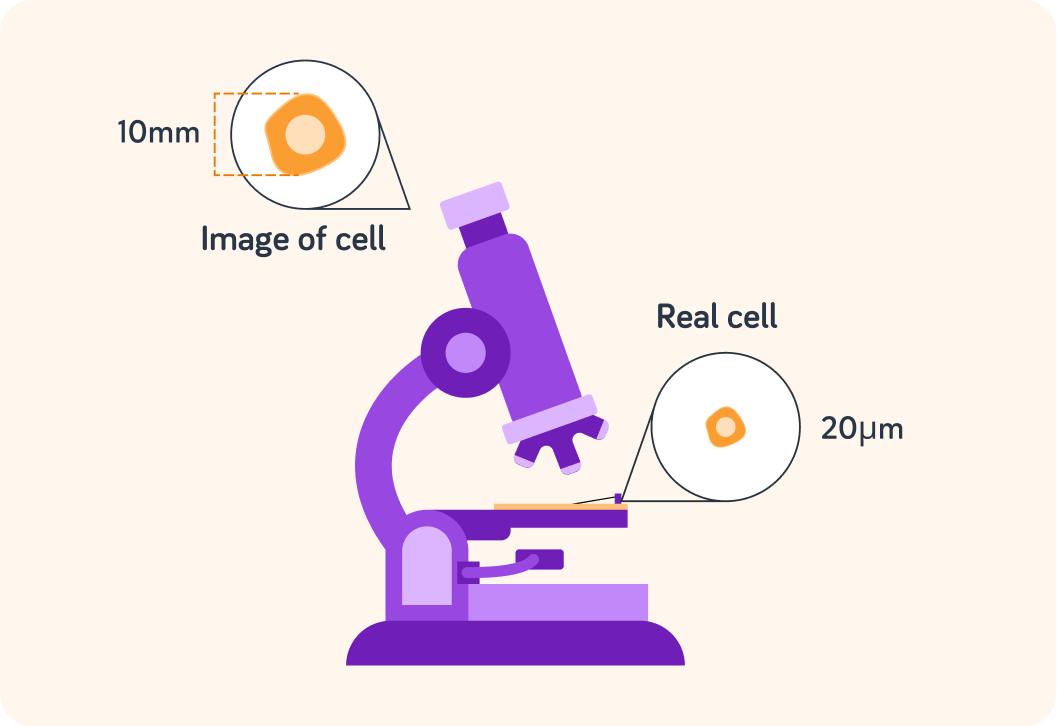
What unit is the size of the image of the cell given in?

Be careful about the units!

If the size of the real object and the size of the image of the object aren't given in the same unit, you have to make them the same unit before you calculate magnification.

What is the magnification here?

Here magnification is $\times 500$

$20 \mu m$ is the same as $0.02 \space mm$ , so $magnification = \frac{10 \space mm}{0.02 \space mm}=500$

Here you have the image size and the magnification

You want to find out how big the cell actually is.

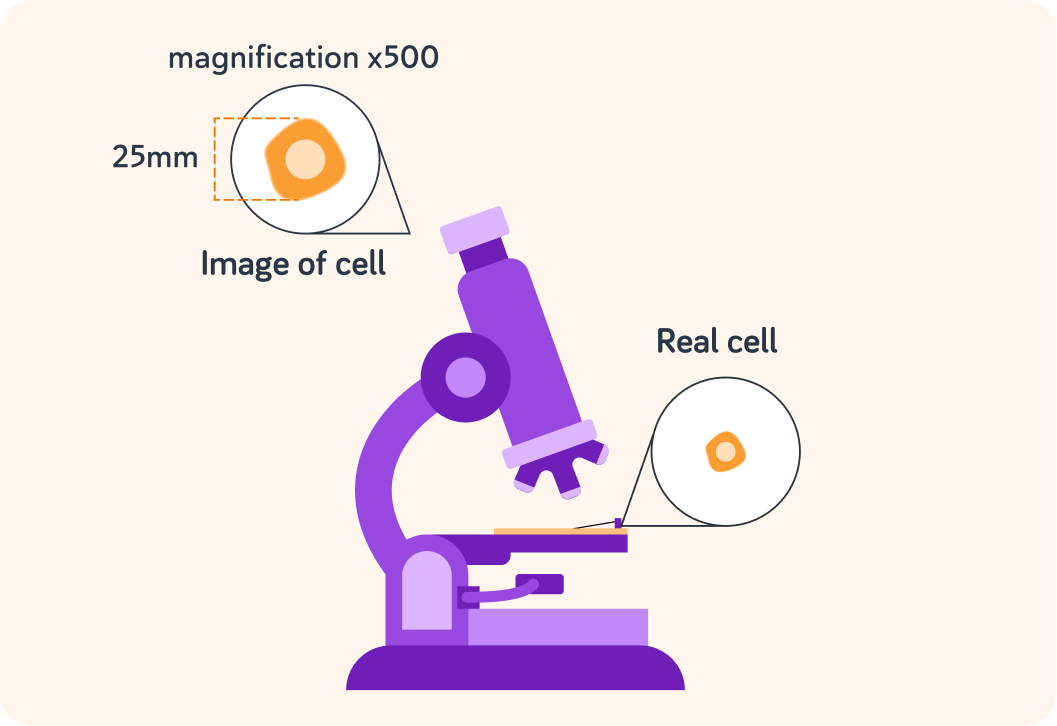
How can you use $magnification = \frac{image \space size}{real \space object \space size}$ to work it out?

A) $real \space object \space size = image \space size \times magnification$ B) $real \space object \space size = \frac{image \space size}{magnification}$ C) $real \space object \space size = \frac{magnification}{image \space size}$

Now, use $real \space object \space size = \frac{image \space size}{magnification}$ to work out how big the cell actually is in $mm$

Here the image of the cell is given in $\mu m$ . What unit is that?

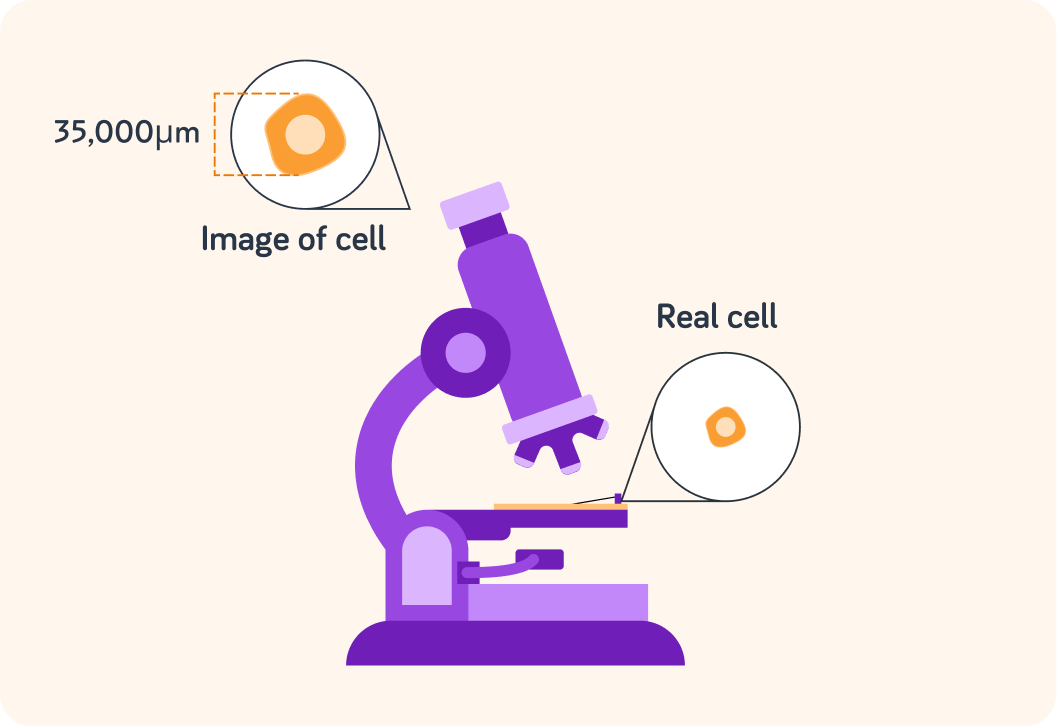
How big is the image of the cell in $mm$ ?

How big is the image of the cell in $cm$ ?

Summary! We use microscopes to study cells and other objects that are very small

Microscopes magnify things - they make them appear bigger.

You calculate magnification like this

$magnification = \frac{image \space size}{real \space object \space size}$

For example

Here the cell appears to be $30 \space mm$ big in the image, but in reality the cell is only $0.03 \space mm$ big. That means the microscope has magnified the cell $\times 1,000$ in the image.

You can also calculate the size of the real object of you have the image size and the magnification

$real \space object \space size = \frac{image \space size}{magnification}$

Remember that the image size and the real object must be in the same unit before you calculate

For example, you can't say $\frac{30 \space \mu m}{30 \space mm}$ to find magnification - one is in micrometres and the other in millimetres!