Number

YOU ARE LEARNING:

Basic Arithmetic

Basic Arithmetic

Addition, subtraction, multiplication and division are called operations. We can use them to manipulate numbers.

These symbols will be familiar to you. How else can we describe them? They are _________

The four operations are:

Addition $+$ Subtraction $-$ Multiplication $\times$ Division $\div$

Starting with addition, what is $17+8$ ?

What if you have $170$ and you add $27$ ?

Let's work it out step by step ➡️

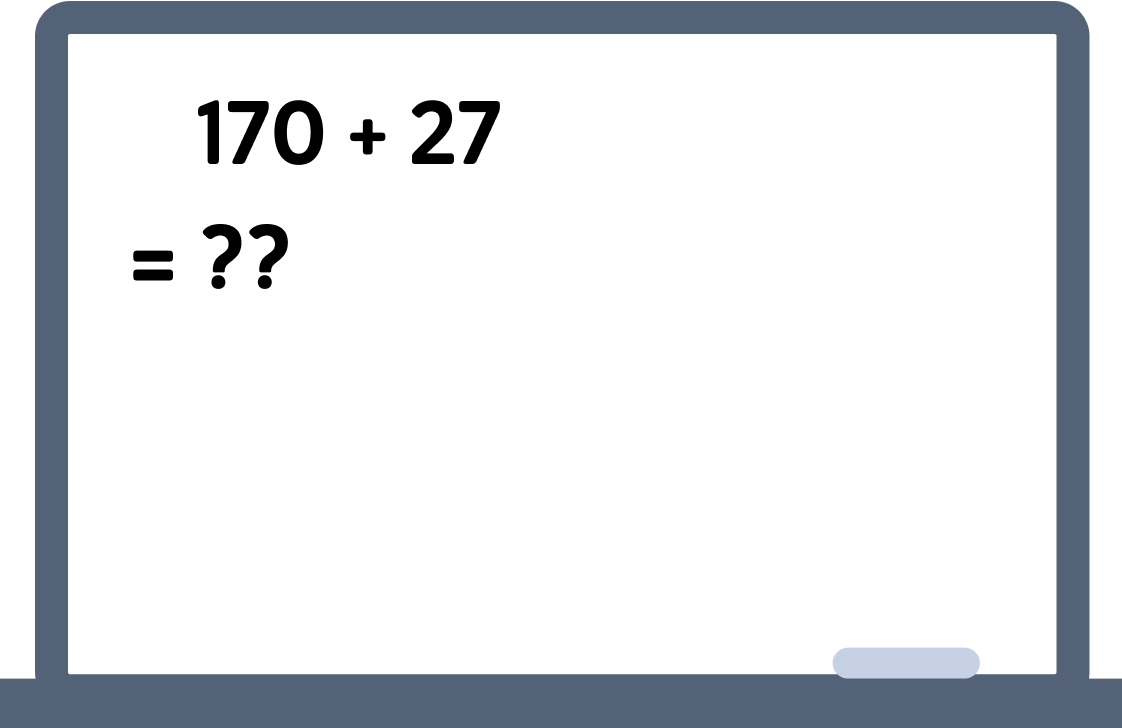
First break $27$ into easier numbers

$27$ is made up of $2$ tens and $7$ units

Add $20$ onto $170$

Now add $7$ to $190$

So in total...

$170+27=197$

Addition is commutative.

The order of the numbers doesn't matter.

What is $14+7$ ?

We've seen that $14+7=21$ . Let's change the order of our sum, what is $7+14$ ?

We have shown that $14+7=7+14$ .

This is true for all additions.

What is $87+115$ ? Remember, if it makes it easier you can work out $115+87$ as addition is commutative.

Sometimes it's easier to add more than we need

then subtract the difference.

What about $143+48$ ?

Let's work it out step by step ➡️

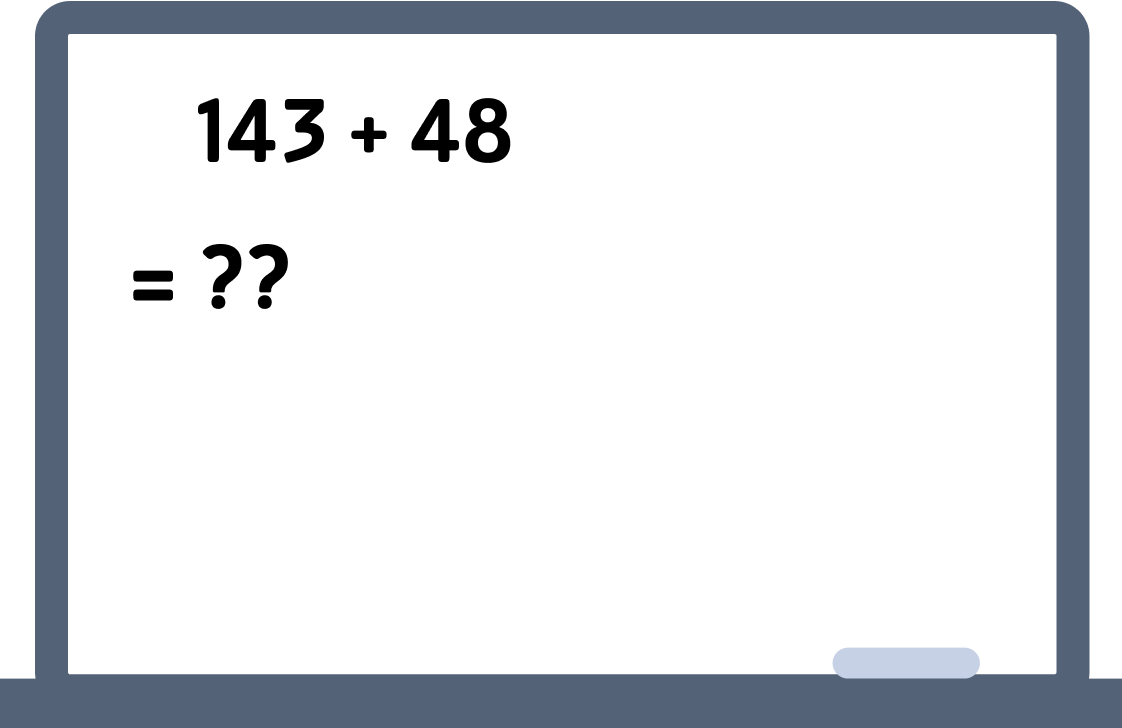
$48$ is two less than $50$

So $48$ becomes $50-2$

Add $50$ to $143$

Now subtract $2$ from $193$

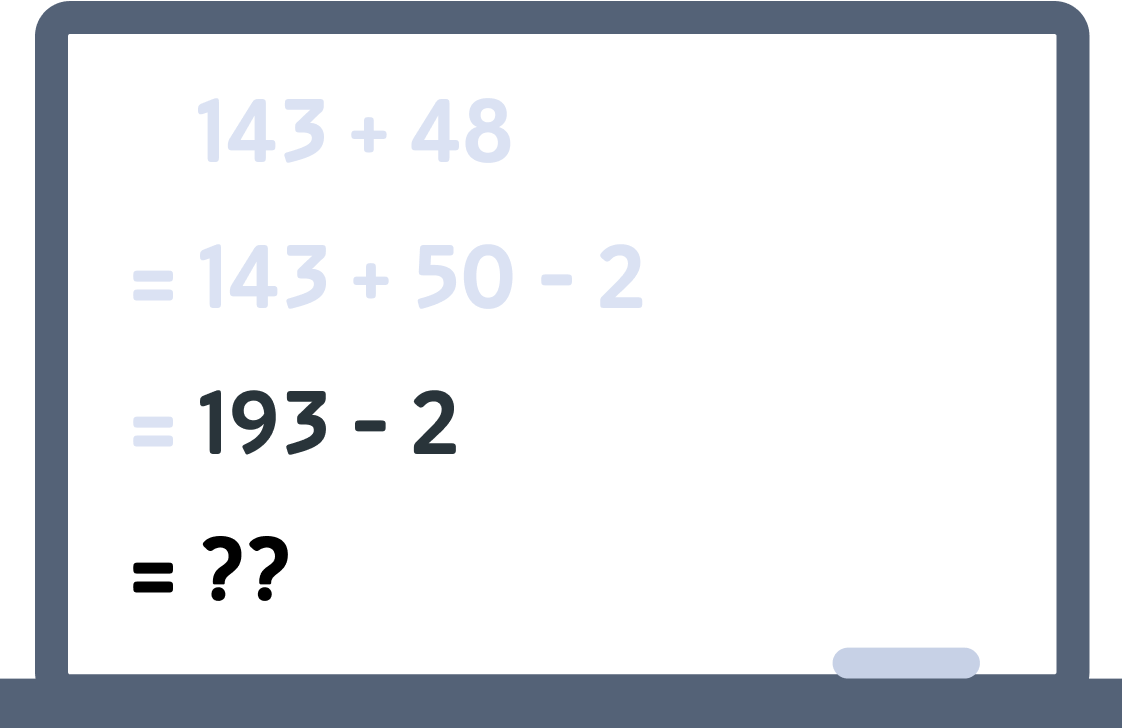
The final answer is $191$

Nice! 👍

What is $122+79$ ?

What is the opposite of addition?

Subtraction has similar strategies to addition

We can also use the words take away or minus for subtraction.

Take care with subtraction, unlike addition it is not commutative.

The order of the numbers matters $14-6=8$ but $6-14=-8$ .

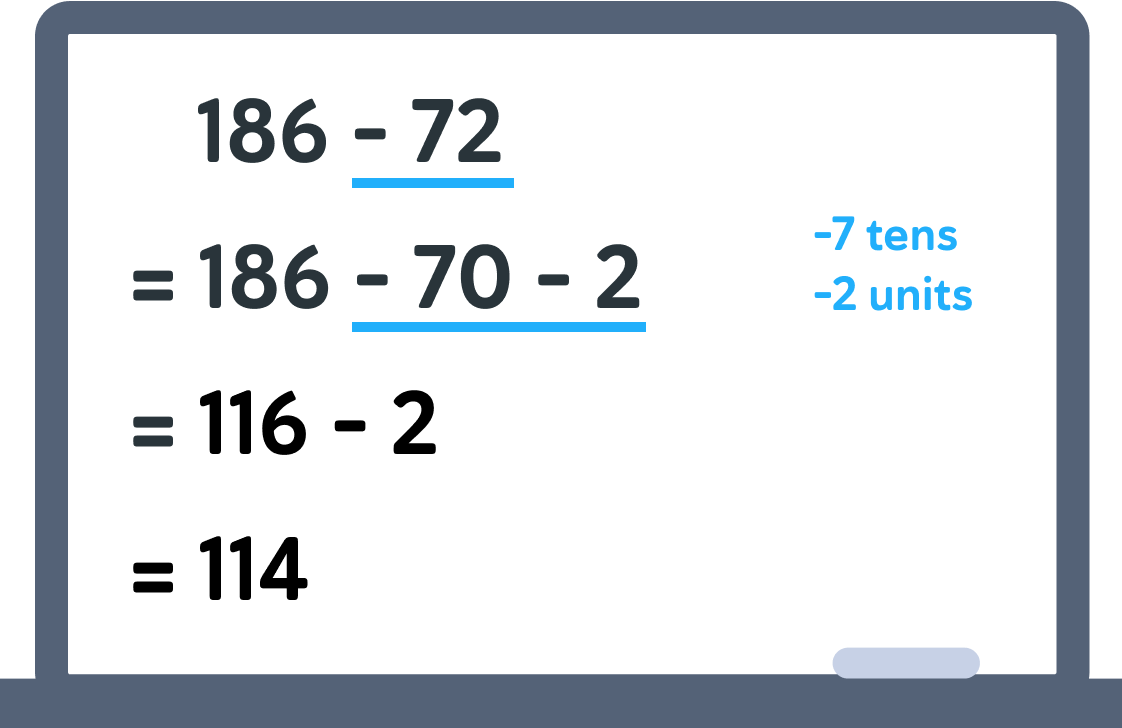
What about $186 - 72$ ?

Let's work it out step by step ➡️

Let's break $72$ into smaller parts

$72$ = $7$ tens and $2$ units

Subtract $7$ tens from $186$

Now subtract $2$ units from $116$

The final answer is $114$

Great work! 👍

Calculate $187 - 53$

What is $203-79$ ?

Multiplication uses our knowledge of times tables. What is $8\times 4$ ?

Let's try a harder multiplication: $17 \times 8$

We can split this into two multiplications

Let's work it out step by step ➡️

Break $17$ into smaller parts $17=10+7$ .

We can then work out $10\times 8$ and add it to $7\times 8$ .

First, work out $10 \times 8$

Now work out $7 \times 8$

Finally, add them together

$80 + 56 = 136$

The final answer is $136$

Nice!

Like addition, multiplication is commutative. What does this mean?

What is $7\times 23$ ? Remember that you can change the order of the numbers if it makes it easier.

What is the opposite of multiplication?

For example: $18 \div 3$

$18$ can be split into groups of $3's$

We use our knowledge of the times tables, in this case $6 \times 3 = 18$

So six groups of three go into $18$ or:

$18 \div 3 = 6$

Work out $45 \div 9$

Which multiplication fact can be used to work out $72 \div 12$ ?

Like subtraction, division is not commutative. The order of the numbers matter. $8\div 4=2$ but $4\div 8=0.5$ .

Summary! The four operations are:

Addition $+$ Subtraction $-$ Multiplication $\times$ Division $\div$

Strategies for addition include:

Splitting a number $170+27=170+20+7$ Adding on more $143+48=143+50-2$

Strategies for subtraction include:

Splitting a number $187-53=187-50-3$ Taking away more $357-49=357-50+1$

Strategies for multiplication include:

Splitting a number $34\times 9=30\times 9+4\times 9$

Strategies for division include:

Use knowledge of times tables $84\div 7=12$ as $7\times 12=84$ .

Addition and multiplication are commutative

The order of the numbers doesn't matter $115+80=80+115$

$15\times 3=3\times 15$

Subtraction and division are not commutative

The order of the numbers does matter $10-2=8$ but $2-10=-8$

$40\div 10=4$ but $10\div 40=\dfrac{1}{4}$