Number

YOU ARE LEARNING:

Relationships between Numbers

Relationships between Numbers

We use a system of notation to indicate whether numbers are equal, greater than or less than each other.

Notation lets us write things without words. There is some maths notation here, how else could we describe them?

These are also symbols. Which one means equal to?

We've seen that $=$ means equal to, but which symbol means not equal to?

The equal sign means that what is on the left side is the same as what is on the right side. Which of these statements is not true?

We saw that the statement $2\times 3=4$ is not true.

But we have another symbol and the statement $2\times 3 \neq 4$ is true.

Which of the symbols means less than?

The opposite of less than is greater than.

The greater than symbol is $>$ . The open end points to the larger part and the closed end to the smaller part.

The symbol $\leq$ is very similar to the less than symbol, $<$ . How does the extra line change it?

We can now give names to all these symbols.

Remember that we read these from left to right in a calculation.

If we have an unknown number which we call $y$ , how can we show that it is not equal to zero?

We often use these symbols when we have an unknown number which we might call $x$ . We might know that it is either greater than or equal to $3$ and so we write:

$x\ge3$

How would you write down " $x$ is greater than $3$ "?

How would you write down " $y$ is less than $15$ "?

What if we wanted to write that our unknown number, $x$ , is less than $8$ but greater than $4$ ?

We can use multiple symbols to achieve this and start with the smallest number.

Which option is the correct statement using symbols to say that $x$ is less than $8$ but greater than $4$ ?

This time, $x$ is greater than $2$ , but less than $10$ . How do you write this using symbols?

We can use symbols to group data together.

The table shows four groups of data about the people's height.

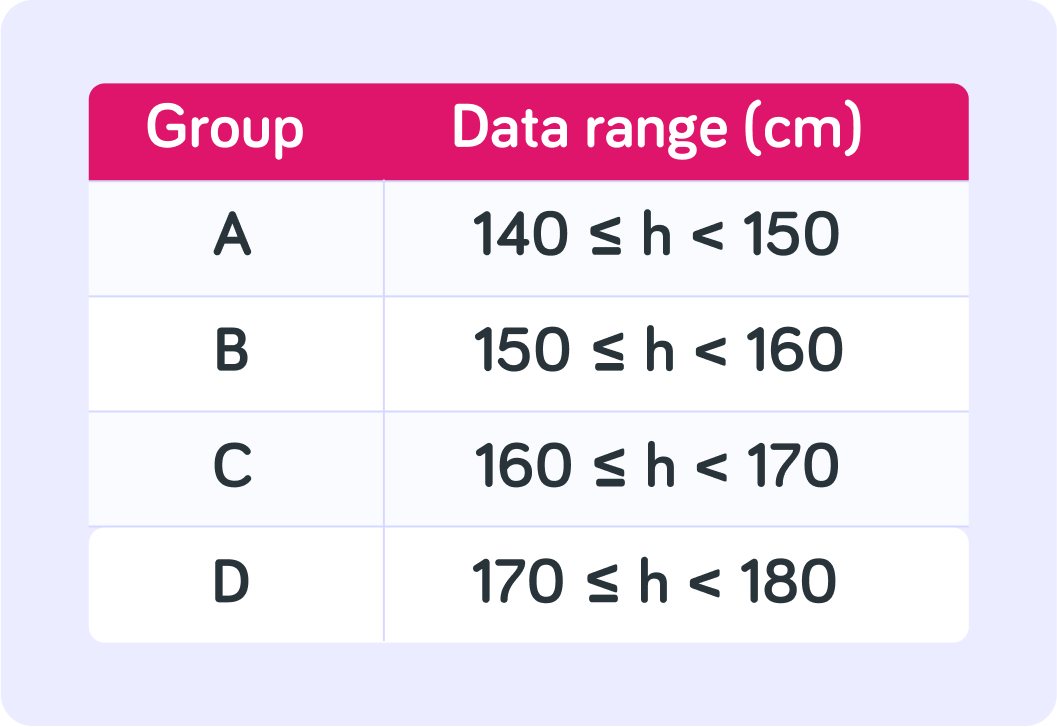
If a person is $155cm$ tall, which group would they be in?

If a person is $170cm$ tall, which group would they be in?

This is where the difference between the symbols $\leq$ and $<$ is important.

When gathering data we need to make sure that each person can only be in one group. Someone who is $170cm$ tall just falls into Group $D$ .

How would you write " $x$ is less than $4$ , but greater than or equal to $2$ "?

In summary...

Symbols are often used when we have an unknown number, $x$ or $y$ or other letter.

Symbols form part of expressions.

The expression $x\neq 2$ means that our unknown number $x$ cannot be $2$ or is not equal to $2$ .

Symbols can be used to show a range of values

No one can be in more than one group so the symbols are used carefully.