Number

YOU ARE LEARNING:

Negative Numbers

Addition, subtraction, multiplication and division of negative numbers requires us to follow certain rules.

Select the two options that are true for negative numbers.

You can select multiple answers

Negative numbers are all the numbers which come before zero.

These continue to infinity in the negative direction.

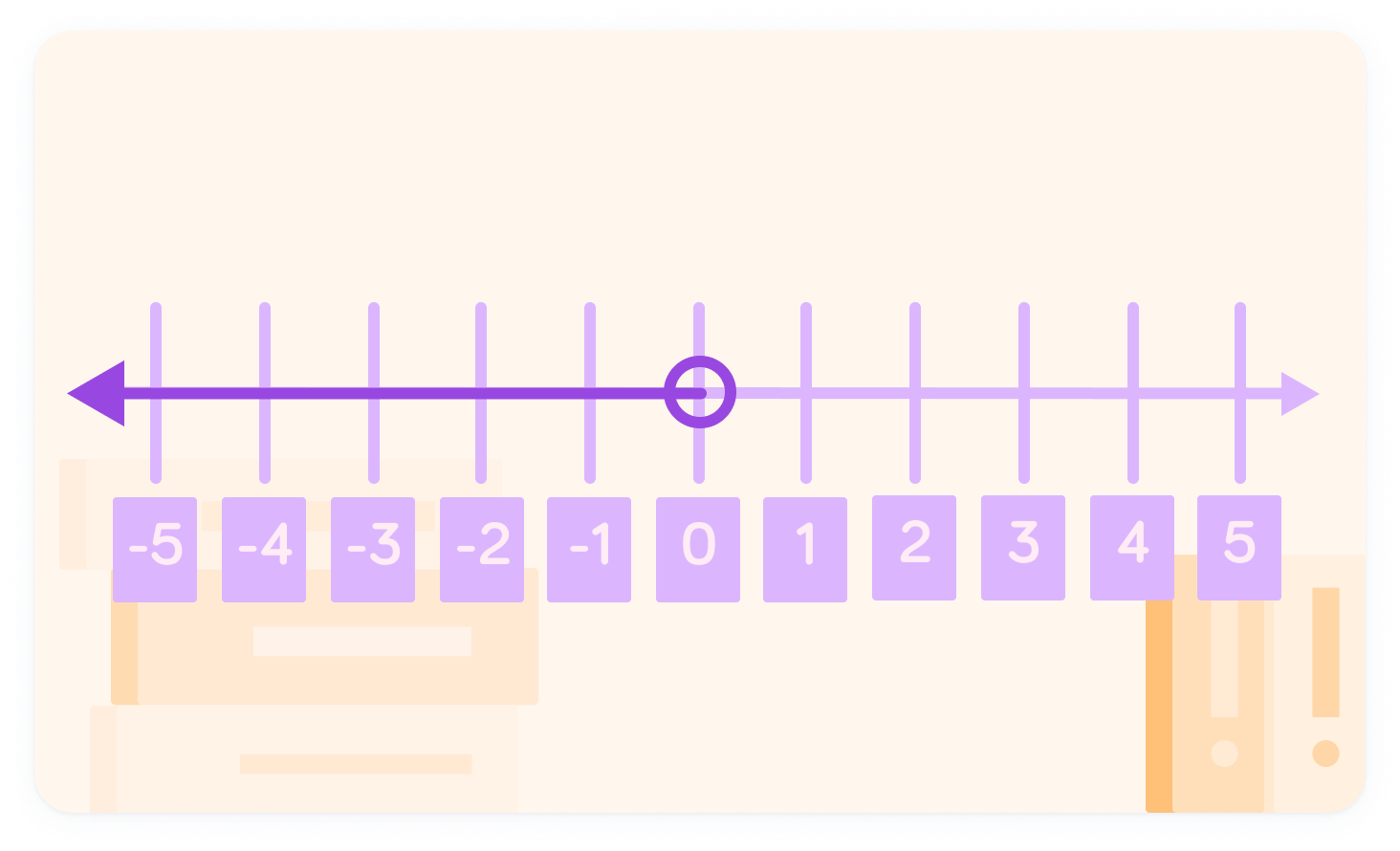
We represent this with an arrow

On a number line, we use the arrow to represent a range of numbers. The open circle shows that zero is not included.

Negative numbers closer to zero are greater

So $-2$ is greater than $-5$ , we can also write this as $-2>-5$ .

Which number is greater: $-4$ or $-3$ ?

Here we subtract from a positive number: $6-11$

Start from $6$ on the number line

Move left, when you have moved five times you are at zero because $6-6=0$

Subtract $5$ more from $0$ by moving another five to the left. What is $0-5$ ?

Nice!

The final answer is $-5$ 👍

Let's look at $6 - 11$ using counters

We start with $6$ positive counters.

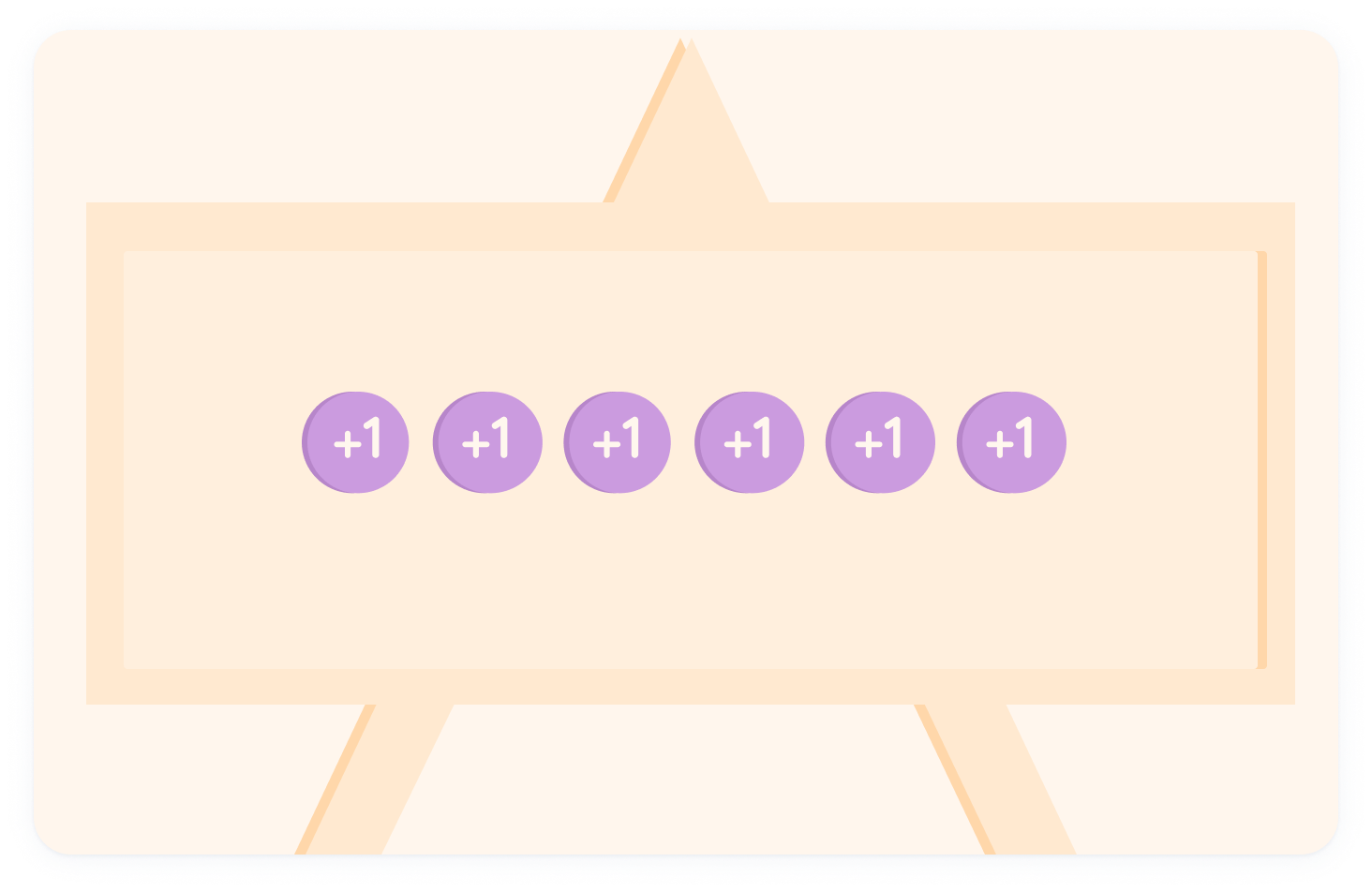
We want to subtract $11$ counters

So we need to include $11$ negative counters.

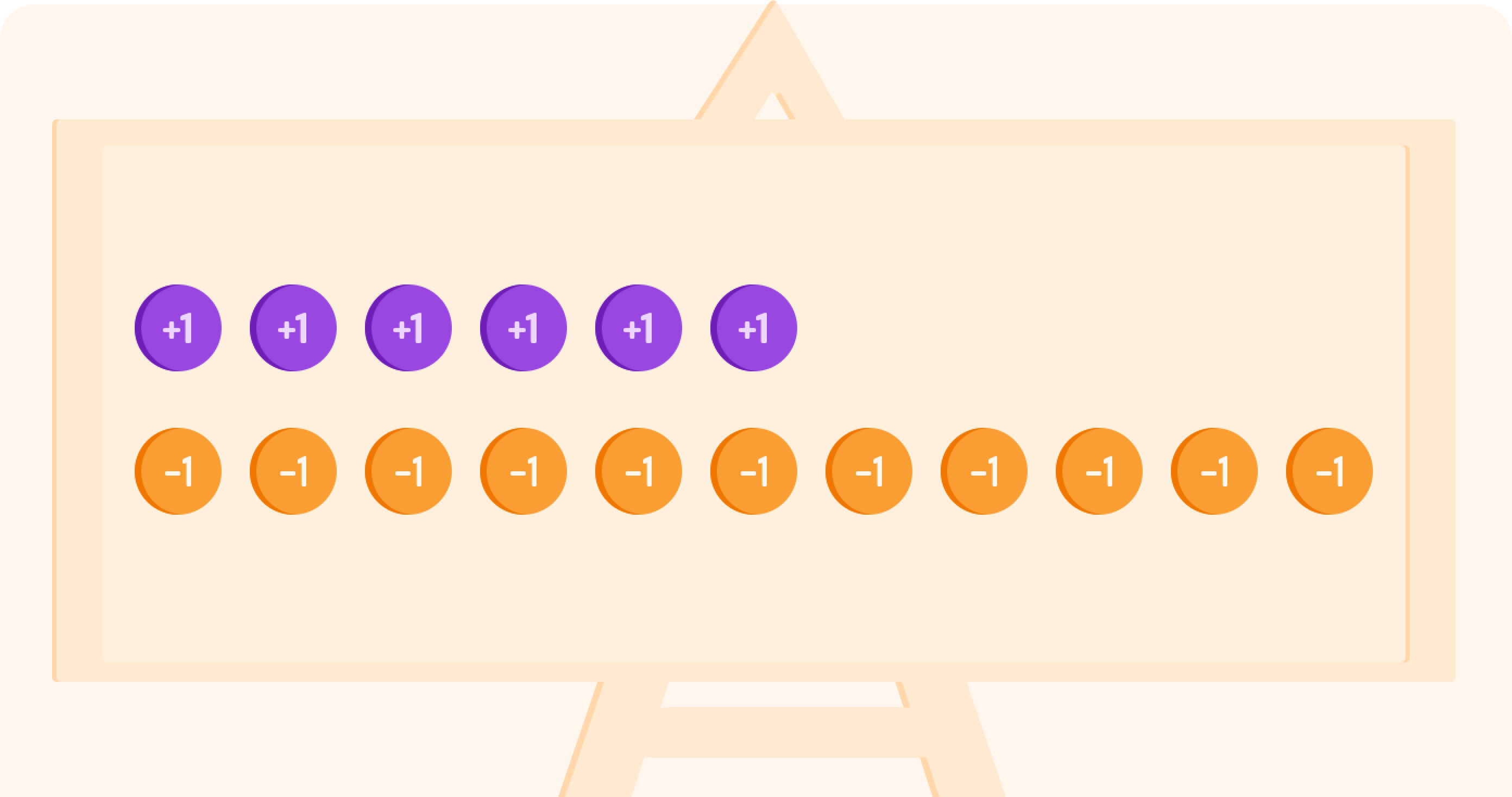
One positive counter and one negative counter make a zero pair.

These cancel each other out as $1-1=0$ .

Now we can cancel out "zero pairs"

This will leave us with five negative counters, so $-5$ .

Let's try adding a positive to a negative: $-5 + 8$

Start at $-5$ on a number line

Adding 8 means to move "right" 8 times

We need to go past zero

This is because $8$ is bigger than $-5$ 's zero pair

What is $-5+8$ ?

Let's have a look at $-5 +8$ using counters

We will start with $5$ negative counters.

Add $8$ positive counters

Now we can see the zero pairs.

Cancel out five zero pairs

We are left with $3$

We can rewrite $-5 + 8$ as $8-5$ and the answer is still $3$ .

This is because addition is commutative.

Commutative means that it doesn't matter what order we put our numbers in, we will get the same answer.

$2+7=9$ and $7+2=9$

When doing this with negative numbers, make sure the negative sign stays with the right number! What is another way of writing $-4+6$ ?

What is $-8 + 5$ ?

Let's now look at subtracting from a negative number: $-2 - 5$

We start at $-2$ on our number line

Subtracting means to move left along the number line

Move $5$ along the number line in the negative direction.

What is $-3 - 6$ ?

Sometimes we will need to subtract a negative number, which will result in two minus signs next to each other:

$3-(-2)$

Subtracting a negative is the same as adding a positive.

So we can rewrite the question as $3-(-2)=3+2$ .

So what is $3-(-2)$ ?

What is $12-(-11)$ ?

What is $53-(-12)$ ?

Adding negative numbers

We may also need to add a negative number, resulting in a plus and minus sign next to each other:

$3+(-2)$

Adding a negative number is the same as subtracting a positive:

$3+(-2)=3-2$ .

What is the answer to $3+(-2)$ or $3-2$ ?

What is $-11+(-7)$ ?

If you multiply or divide two negative numbers then the answer will always be...

What is $-6\times-3$ ?

What is $\dfrac{-21}{-7}$ ?

In multiplication and division,

if only one number is negative then the answer is always negative.

What is $-6 \times 7$ ?

What is $\dfrac{-50}{5}$ ?

Summary!

Negative numbers sit to the left of zero on a number line.

For example, $-3$ is a negative number.

Move left on the number line when adding a negative number.

This is the same as subtracting a positive number. $6+(-2)=6-2=4$

Move right on the number line when subtracting a negative number.

This is the same as adding a positive number. $(-8)-(-10)=(-8)+10=2$

Multiplying and dividing:

When both numbers are negative, the answer is positive. $(-2) \times (-3) = 6$

Multiplying and dividing:

When one number is negative and the other positive, the answer is negative. $18 \div (-3)=-6$ .