YOU ARE LEARNING:
Surds: Basics

Surds: Basics
Surds are irrational roots, which can be multiplied and divided using certain rules.
A surd is a root of an integer that is irrational.
21, 17, 745 and 0.34 are all examples of rational numbers because they could be written as fractions.
Is 109 rational?

9=3 is a rational answer, as it gives an integer.
We cannot write 10 as a rational number, so we call it a surd.
2, π and 30 are all examples of surds as they cannot be written as exact fractions.
Which of the following is a surd?

We can simplify surds by splitting into two factors. One should be a perfect square number, and the other a surd.
ab=a×b
We can understand this better using indices.
ab=(ab)21=a21×b21→a×b
Let's simplify 18
Think of two numbers that multiply to make 18
We have 1×18 or 2×9 or 3×6.
Which multiplication fact above contains a square number?

So, we can split 18 into two different roots
18=2×9=2×9
What is 9?

We now have 2×3
This can be written as one mixed surd: 32
This is the simplest version
18=32
Nice! 👍
Express 72 in the form a2.
Think of factors that multiply together to make 72.
Hang on - this question gives us a hint, one of the factors of 72 must be 2 as it's in the final form!
If 2 is one factor of 72, what must the other factor be?

This leaves us with two roots
We have: 72=36×2=36×2
Simplify 36

Finally, express 362 in the form a2

This is the simplest form!
72=62
Great work! 😃
Simplify 63

Key rule: to divide, divide the numbers in the root
ba=ba
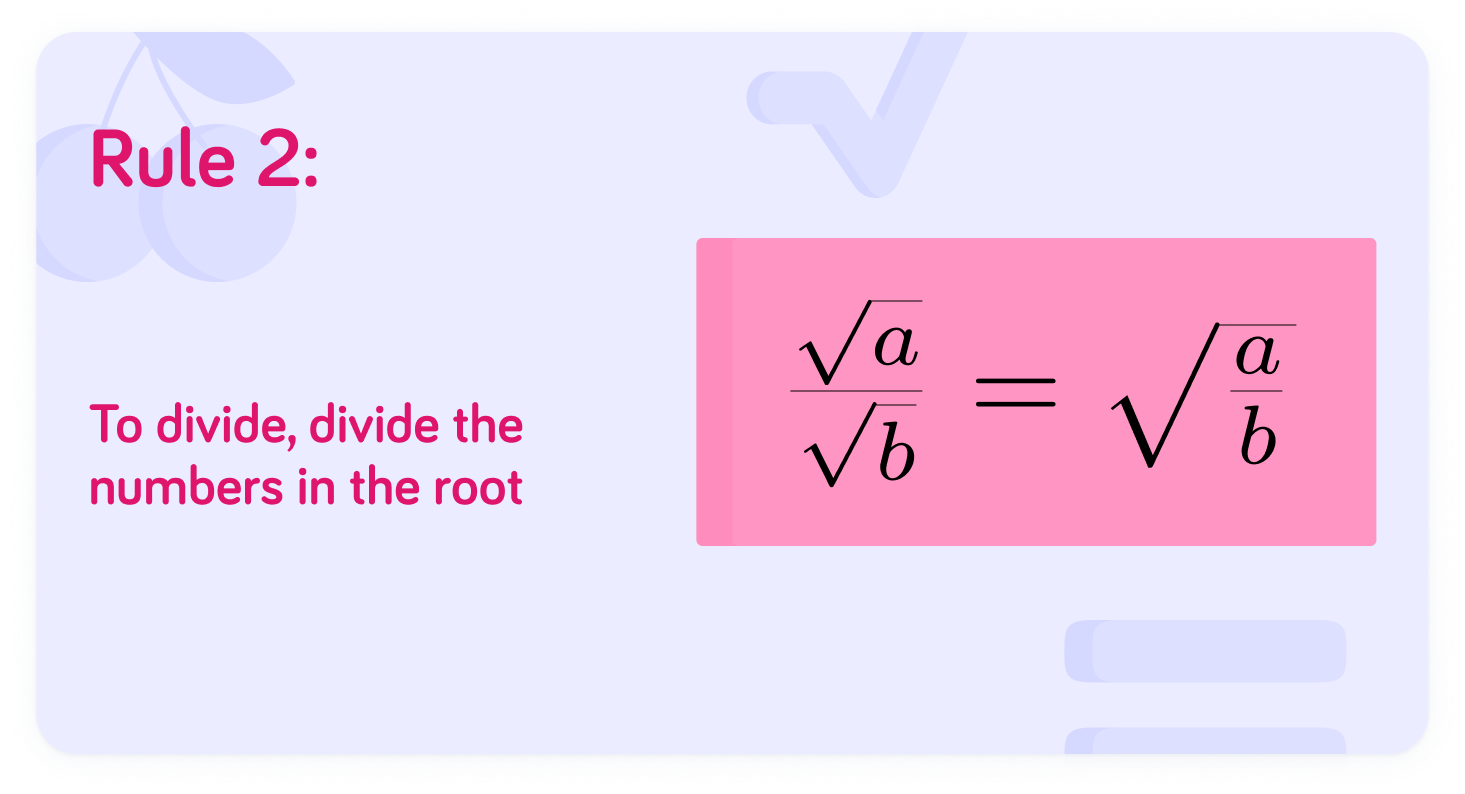
So:
2×5=2×5=10
As with normal numbers, we are able to calculate with surds too. There are a couple of important rules we will need to learn when dealing with surds.
What is 12×5 as a single square root?

What is 1545 as a single square root?

Key rule: to multiply, multiply the numbers in the root
a×b=a×b

Which of the following is not a surd?

