Number

YOU ARE LEARNING:

Surds: Multiplying and Dividing

We can multiply and divide surds together, to form new surds.

We can calculate with surds, subject to a few rules.

To multiply, multiply the numbers in the root

$\sqrt{a}\times\sqrt{b}=\sqrt{a\times{b}}$

So:

$\sqrt3 \times \sqrt6 = \sqrt{3 \times 6} =\sqrt{18}$

What is $\sqrt{2} \times \sqrt{5}$ ?

What is $\sqrt{12} \times \sqrt{5}$ as a single square root?

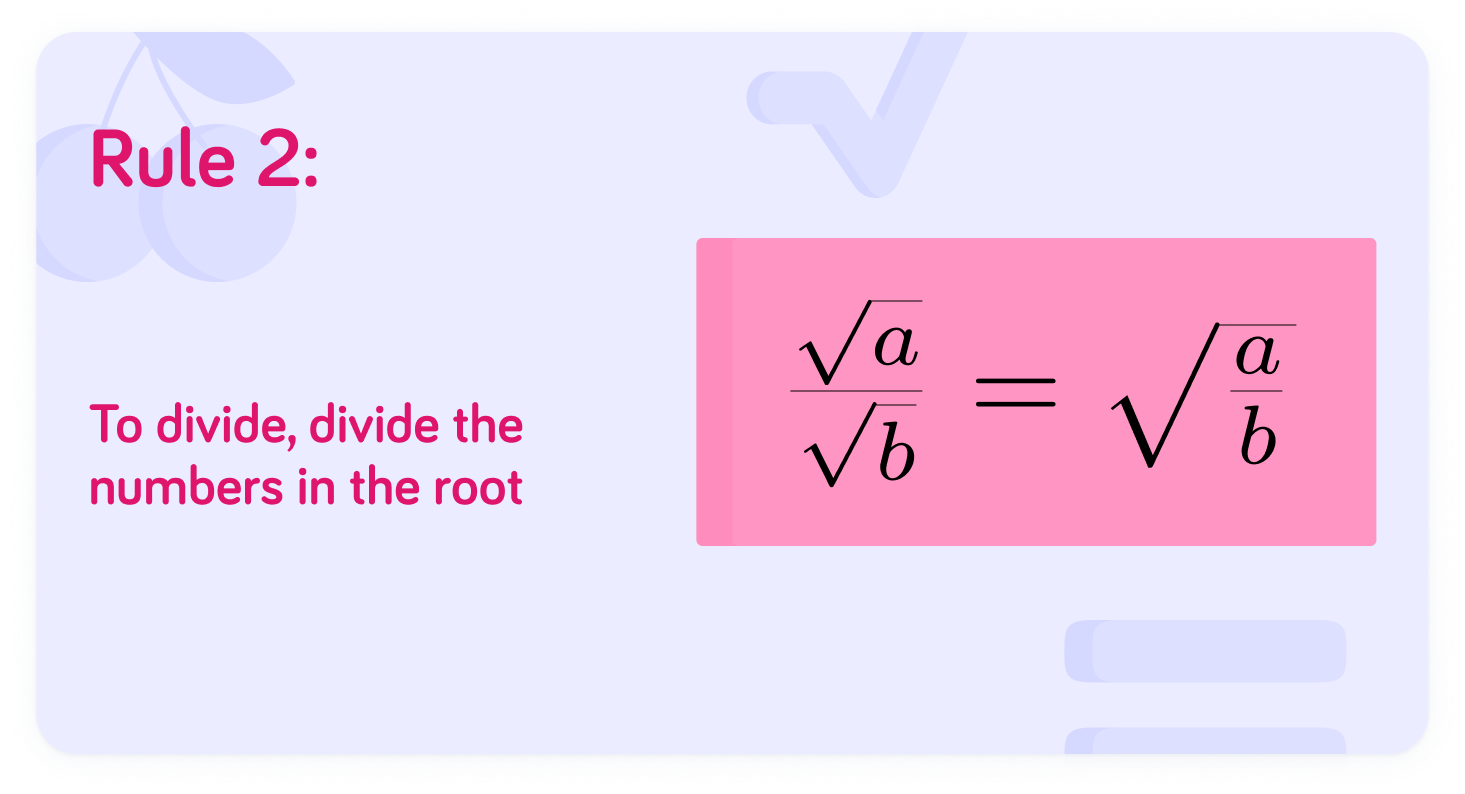
To divide, divide the numbers in the root

$\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$

Therefore:

$\dfrac{\sqrt6}{\sqrt2} = \sqrt{\dfrac{6}{2}} = \sqrt3$

What is $\dfrac{\sqrt{45}}{\sqrt{15}}$ as a single square root?

We can also multiply and divide mixed surds, like those below, by operating on the number and surd parts separately.

$3\sqrt{5} \times 7\sqrt{6}$

Let's find:

$3\sqrt{5} \times 7\sqrt{6}$

Multiply the numbers together: $3 \times 7$

Now multiply the surds $\sqrt{5} \times \sqrt{6}$

Put these two parts together

The final answer is $21\sqrt{30}$ . This can't be simplified, as 30 does not have a factor that is a square number.

What is $24\sqrt{10} \div 8\sqrt{5}$ ?

Find $3\sqrt{5} \times 4\sqrt{3}$

Let's try a division:

$16\sqrt{4} \div 4\sqrt{2}$

Treat is as two separate divisions

$16\div4$ and $4\div2$ .

Find $16\div4$

Find $4 \div 2$

Put these two parts together

The final answer is $4\sqrt{2}$ .