YOU ARE LEARNING:
Sampling

Sampling
Usually, we can't test the whole population. We use sampling to take a section of the population to allow us to estimate characteristics of the whole.
A sample is a section of the total population which we can use to find out information about the whole. Choosing the right sample is extremely important in order to prevent bias.
The first stage of research is to come up with a hypothesis. A hypothesis is a proposed statement that needs to be tested for further validation.
For example, when investigating plant growth, a hypothesis might be "If I keep increasing the amount of sunlight, the plant will continue to grow faster."
It is important, then, to define the population for your hypothesis. The population is the whole group on which you are trying to find out information.
Let's have a look at an example. There are 200 Year 9 students at Appleton School and the headteacher wants to find out their favourite subject.
What is the population?

Could we test the whole population?
Asking every student would be the most accurate method. But, this would be very time-consuming!
We need to choose a sample
A sample is a selection from the total population. The larger the sample size, the more accurate the results are likely to be compared to the total population.
Test the sample and apply to the population
Once we have collected data on the sample group, we can infer information on the whole population in proportion.
Which of the below would be the most accurate sample size in a population of 200 students?

Sample size is important in order to accurately represent the whole of the population. With small sample sizes, there is a greater chance of seeing extreme results.
The whole population of students could look like this
Depending on the size of the sample we collect, we could end up changing the relative amounts of each subject. This would not reflect the real population.
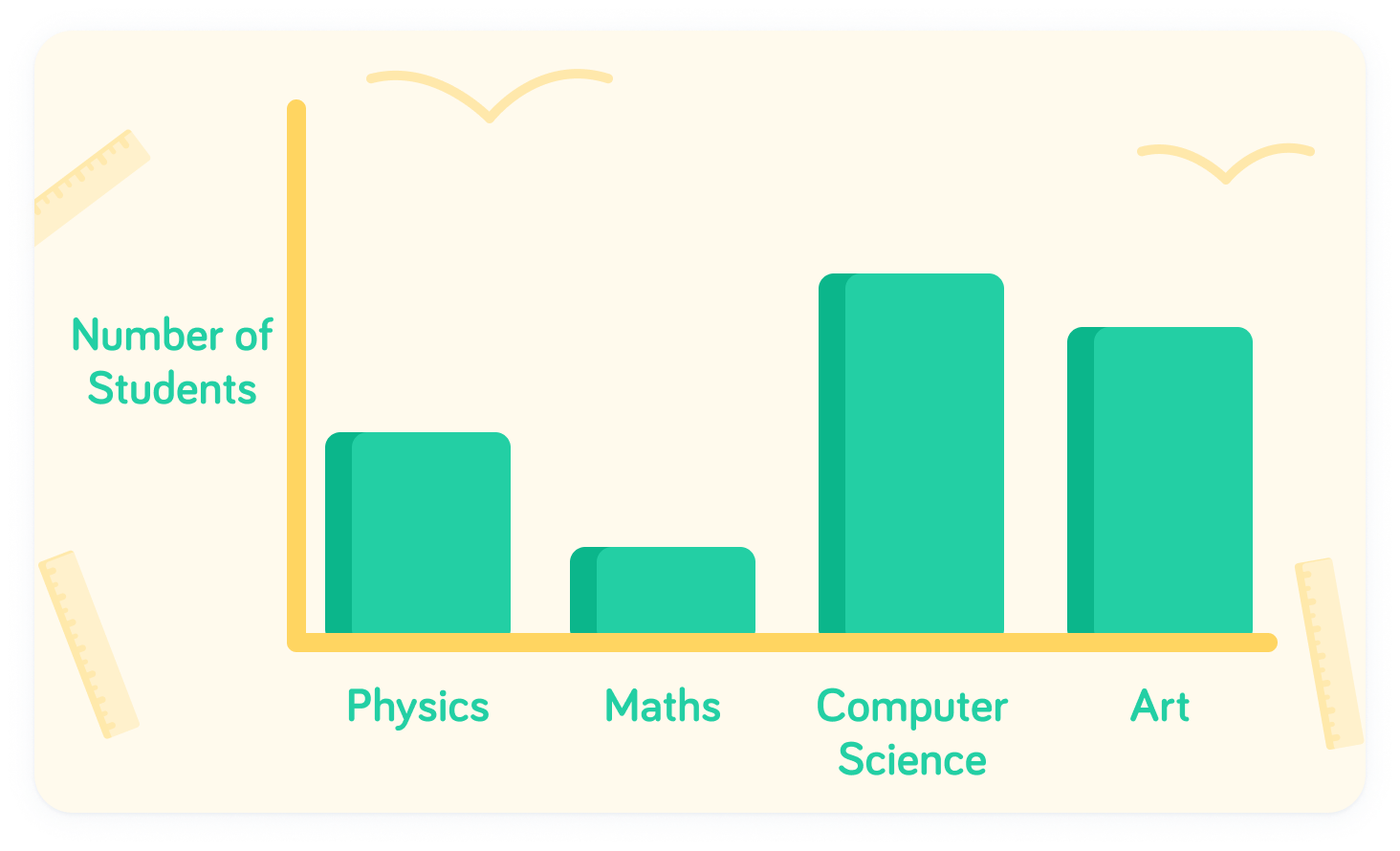
Small samples can lead to extreme results
A small sample of 10 may have a higher proportion of students who prefer Art. The key is that this is more likely to happen with smaller sample sizes.

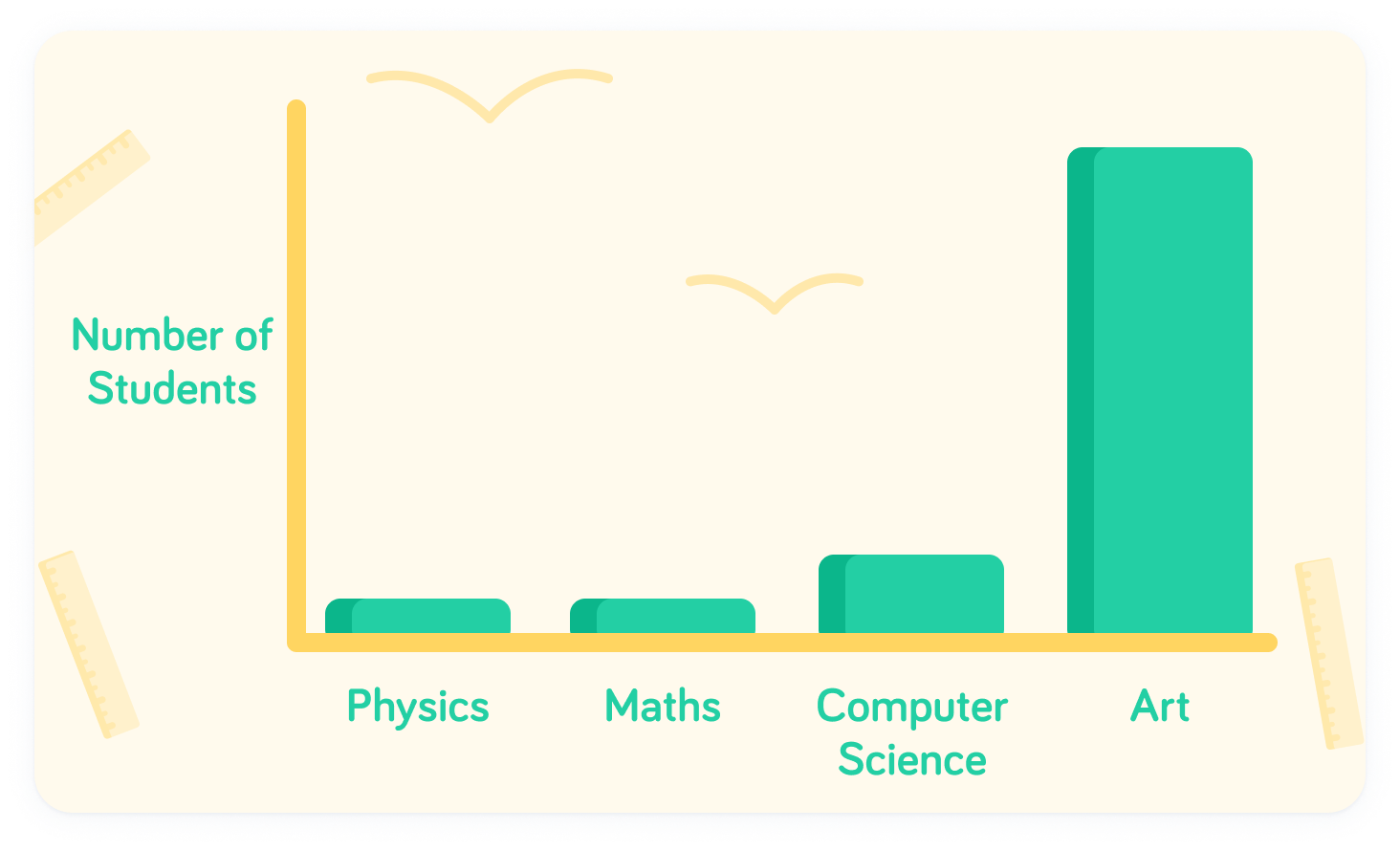
Bias can also affect the reliability of a sample
For example, surveying the students that go to Art club may lead to a larger proportion of students choosing Art as their favourite subject.
Phoebe conducts a survey on how much time people spend at the library every week. She stands at the entrance of the local library and asks the first 10 people she sees entering the library. What two things are wrong with this method?

You can select multiple answers
