Forces in Motion

YOU ARE LEARNING:

Calculating the Moment of a Force

We can use an equation to calculate the moment of a force (size of the rotation).

If you want to lift something using a lever, is it easier to do it with a "longer" or "shorter" lever?

If you only had a short lever, what would you have to do to lift a heavier object?

If you use a lever of length 3 metres to lift a weight with a force of 3 Newtons, what is the moment?

In order to lift something using a lever, we are using a turning force (moment). We can affect the moment by changing the distance or the force applied. Remember the formula $m=F\times d$ where $m$ is the moment in Newton meters, $F$ is the force in Newtons and $d$ is the distance from the pivot in meters.

This image shows the moment formula for a spanner.

Remember the different units for each factor: $m$ is the moment in Newton meters, $F$ is the force in Newtons and $d$ is the distance in meters.

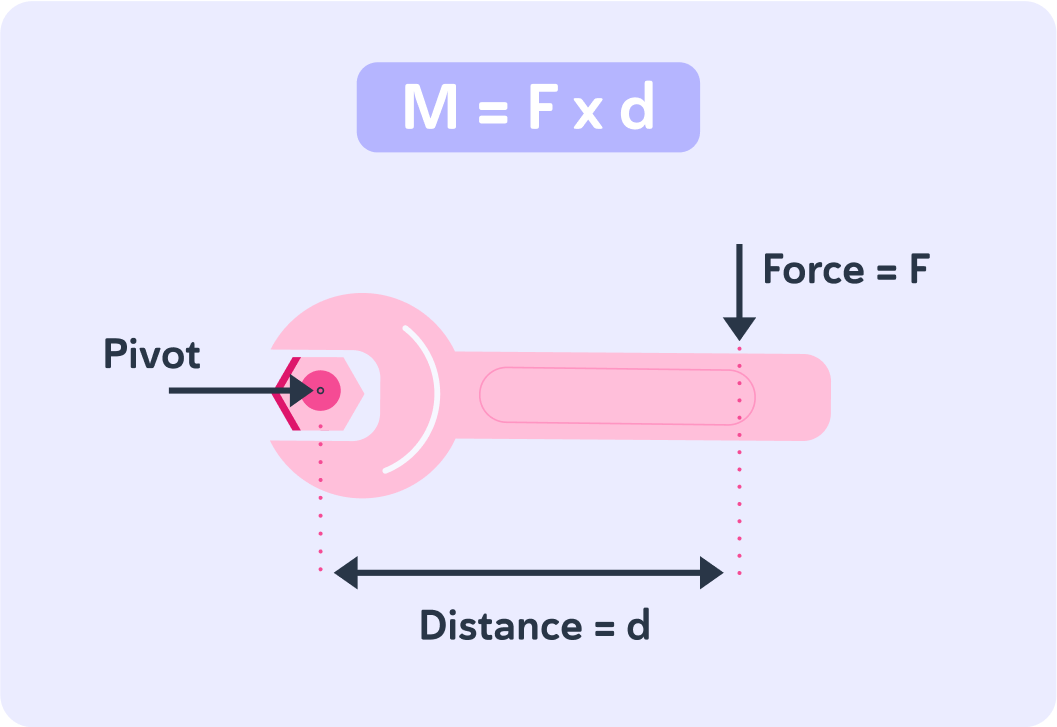
What is the moment around a spanner of length 0.5 metres with a force of 3 Newtons?

What is the moment a person applies on a see-saw if they weigh 900 Newtons and sit 1 metre away from the pivot?

If a person sitting on a see-saw exerts a moment of 500 Newton metres in an anticlockwise direction, what moment does the person on the other side need to exert to balance the see-saw?

What can the bigger child on the see-saw do in order to balance the see-saw?

A) Get off the see-saw B) Move further away from the pivot C) Move closer to the pivot

Answer A, B or C

What does the value of F need to be to ensure the moments on this system are balanced?

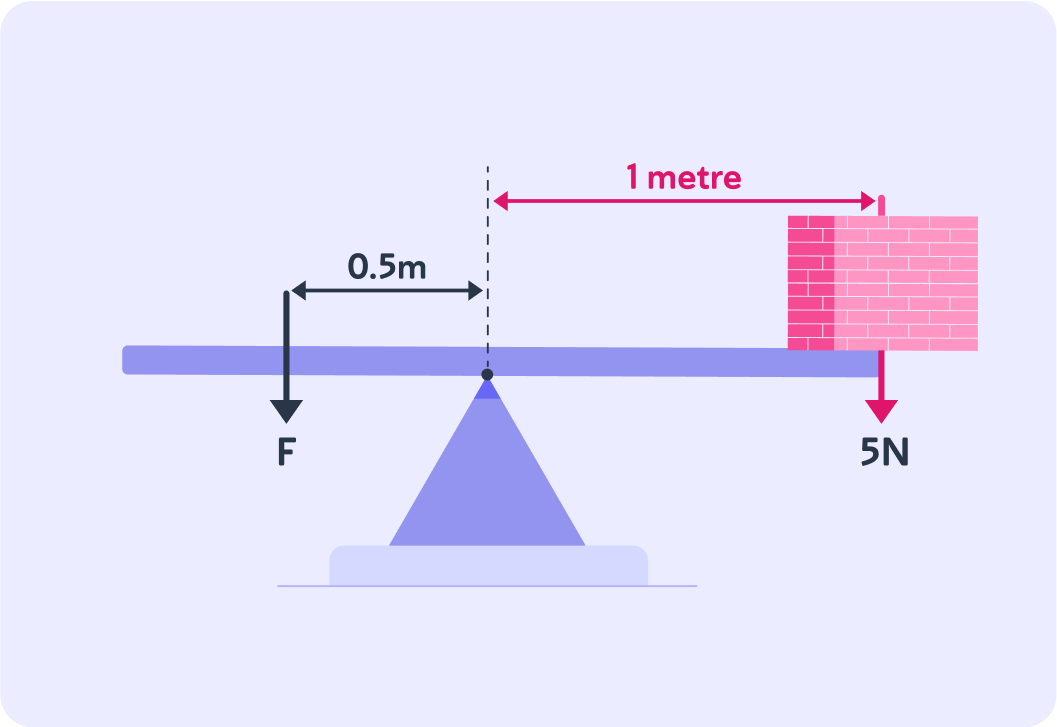
When you need to balance moments on either side of the pivot, you treat the left-hand side and right-hand side as separate entities. You work out each, before finding the values you need to make sure they are balanced.