Forces in Motion

YOU ARE LEARNING:

Gears and Levers

We can use certain tools to transmit the rotational effects of forces, and in this lesson we will see how this is done.

What 3 things are needed for a lever to be used effectively?

You can select multiple answers

This image shows a simple lever being used to lift a load.

It has a load, a pivot and effort is being exerted.

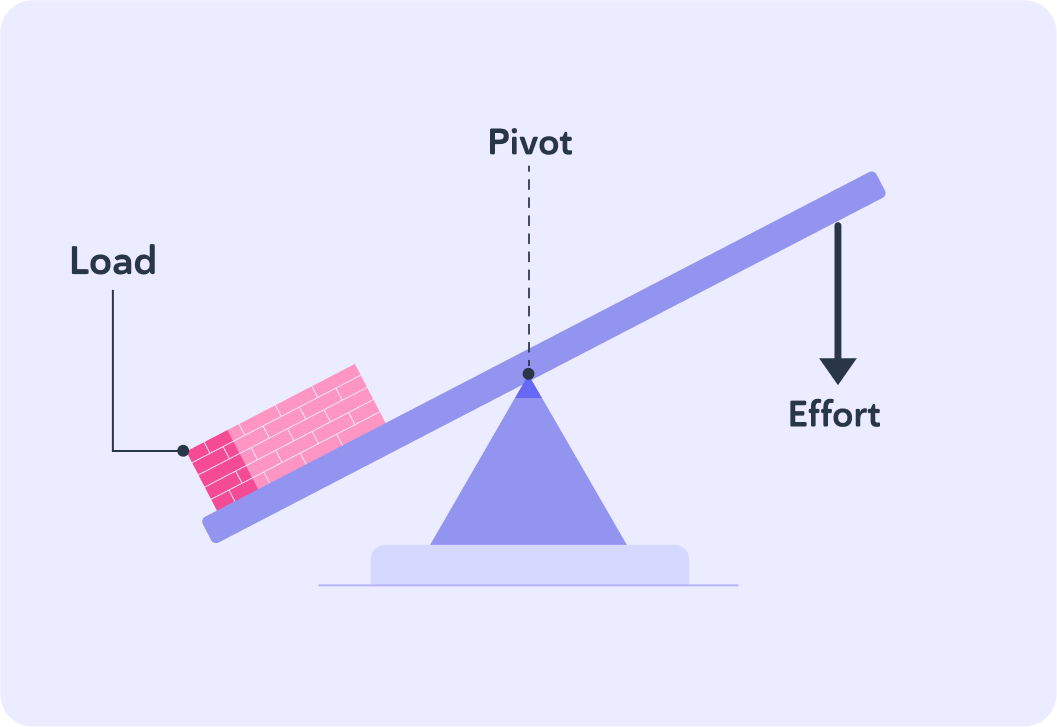
If you increased the distance between the pivot and the place on the lever where effort was being exerted, would you be able to lift "more" or "less" load?

If you chose a longer lever, you would need _____ force to lift the load.

Moment is a rotational force. Recall that $m=F\times d$ , so if we increase distance $d$ , we can afford to reduce effort or force $F$ to lift the same amount of load, or the other way around. We need to create a moment which is greater than the moment created by the load in order to lift the load.

Is a door easier to open closer to, or further away from the hinge?

If a door handle is placed closer to the hinge of a door, will it require more or less force to open the door?

A door works on the same principles as a lever. In order to open the door you need to create a moment to overcome the friction. Because $m=F\times d$ , the greater the distance the less force you need to apply to overcome the friction and open the door.

What is the role of gears in machines, like bikes or cars?

The image above shows a simplified version of a gear.

The forces acting on both cogs is the same, but the moments will be different.

If a smaller cog is driven by a larger cog the larger cog will rotate quickly, but will it have a larger or smaller moment (turning force)?

This is why when you are riding a bike or driving a car you use larger gears for higher speeds as there is less force needed to be applied.

You need to be in smaller gears to begin with to overcome the force to build up the speed as smaller gears have larger moments.

A gear involves two cogs with teeth which lock together and allows us to produce a larger turning force (moment) from a smaller input force.

The smaller wheel turns quickly, but with a smaller force, which turns the larger cog in the opposite direction with a greater force.

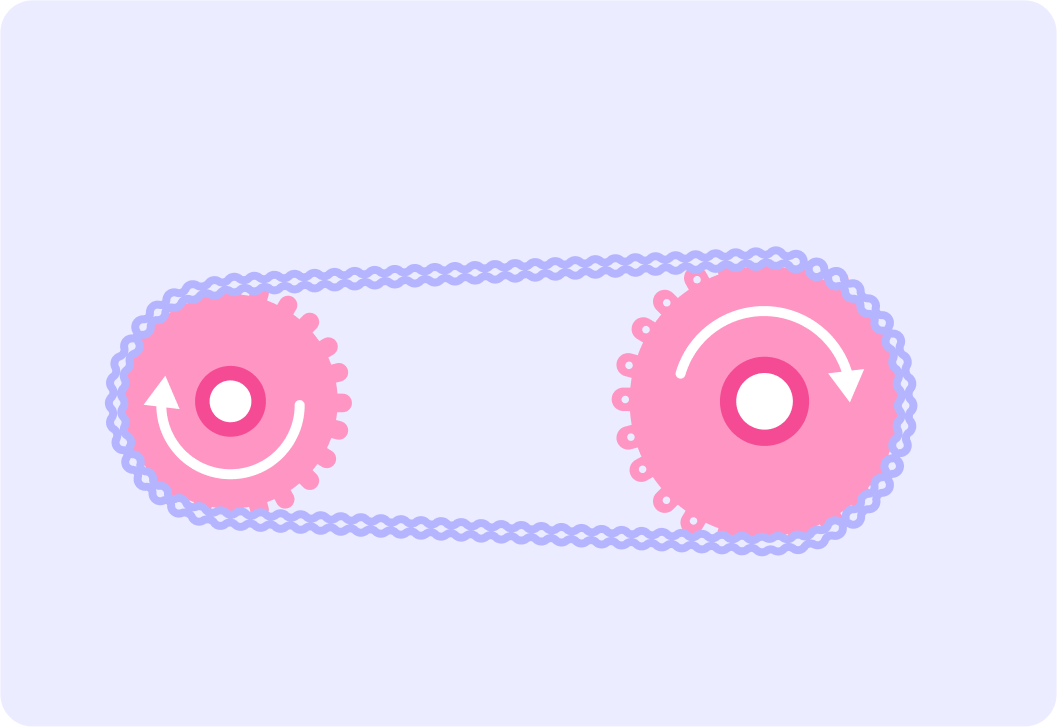
This image shows two cogs of a gear connected on a bike.

The rider's force drives the larger cog so a "rotational force" is transmitted to the smaller cog and to the rear wheel of the bike which is amplified compared to the original force applied.

A gear with a radius of 0.2 m is turned by a gear with a radius of 0.1 m. The moment of the smaller gear is 40 Nm. Calculate the moment of the larger gear.

The first thing you have to do is calculate the force on the smaller gear. What is this?

Now you calculate the moment on the larger gear