Algebra

YOU ARE LEARNING:

Arithmetic Sequences 1

Arithmetic sequences are sequences where the difference between terms in the sequence are the same each time. Finding an unknown term in the sequence is called finding the nth term.

Is there a pattern in this sequence of numbers? Answer yes or no.

How big is the difference between $5$ and $8$ ?

How big is the difference between $8$ and $11$ ?

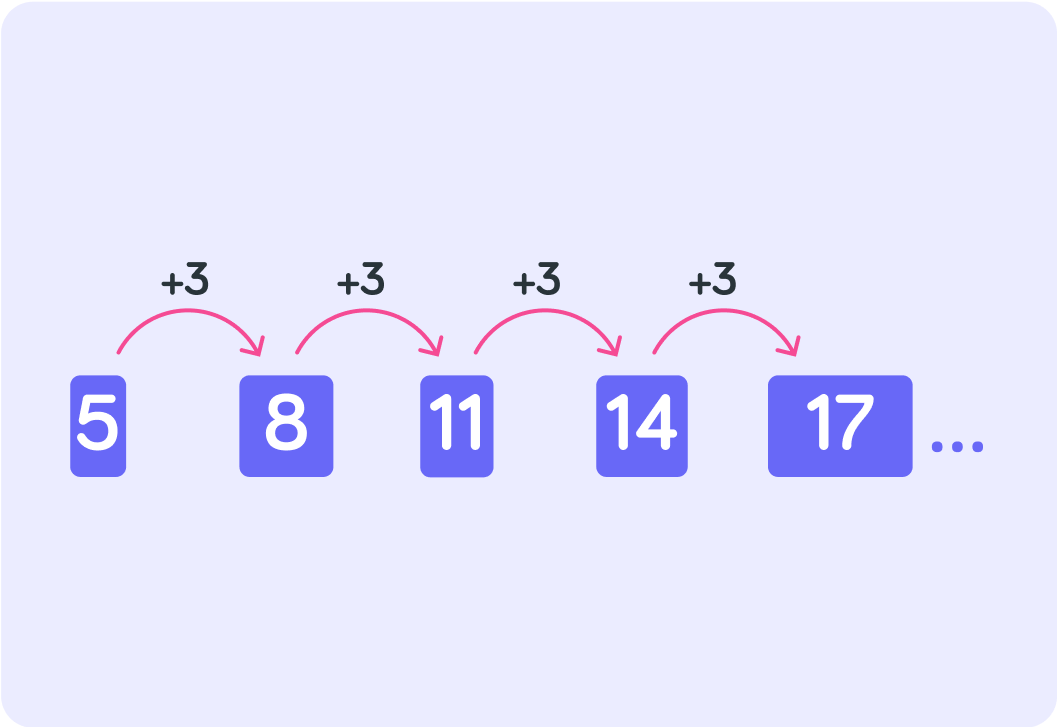
This is an example of an arithmetic sequence

There is a constant pattern in the sequence of numbers. The difference between each number and the following number is $+3$

Is this an arithmetic sequence? Answer yes or no.

This is not an example of an arithmetic sequence

The numbers appear more or less random. There is no constant pattern in the sequence.

Is this an arithmetic sequence? Answer yes or no.

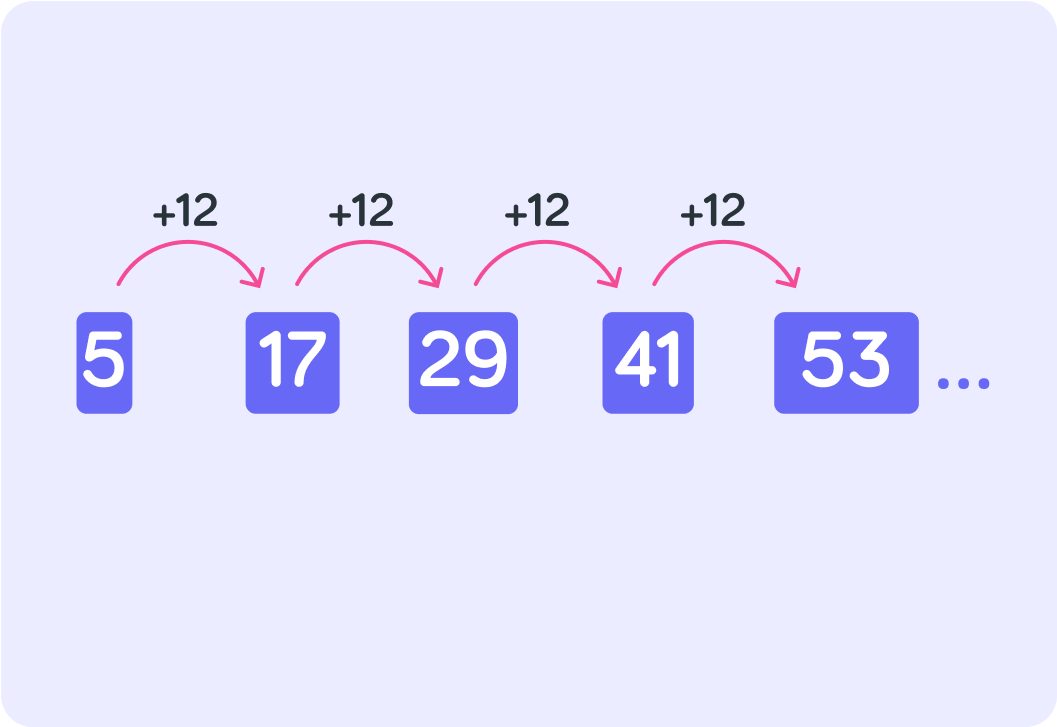
This is an example of an arithmetic sequence

There is a constant pattern. Each number is followed by a number that is $+12$ greater.

What is the next term in this sequence? $4 \space\space\space 13 \space\space\space 22 \space\space\space 31 \space\space\space 40 \space\space\space ...$

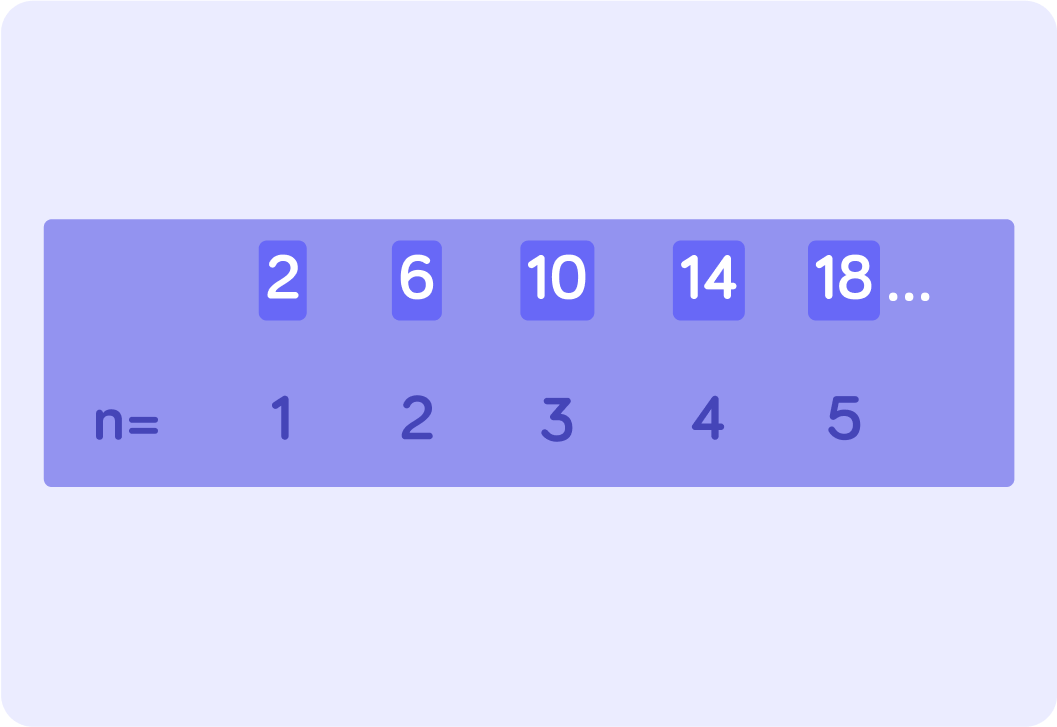
How many terms are listed in this sequence?

There are 5 terms in this sequence

You can label them term number $1$ , $2$ , $3$ , $4$ and $5$ and call that number label $n$

What would be the 6th term in this sequence?

It's probably not hard to find the 7th, 8th and 9th terms either

But what if you wanted to find the 100th term?!

You can work out a formula that helps you find the value of any nth term in this sequence.

To work out this formula, you have to go through a few steps

First you work out how much bigger the value of the term gets every time $n$ gets 1 bigger.

What is the value of the term when $n=1$ in this sequence?

What is the value of the term when $n=2$ ?

How much bigger does the value of the term get every time $n$ gets $1$ bigger?

Every time $n$ gets one bigger the value of the term gets $+3$ bigger

So the first part of your formula is $3n$

But $3n$ is not the finished formula! You can call the missing piece of the formula $x$

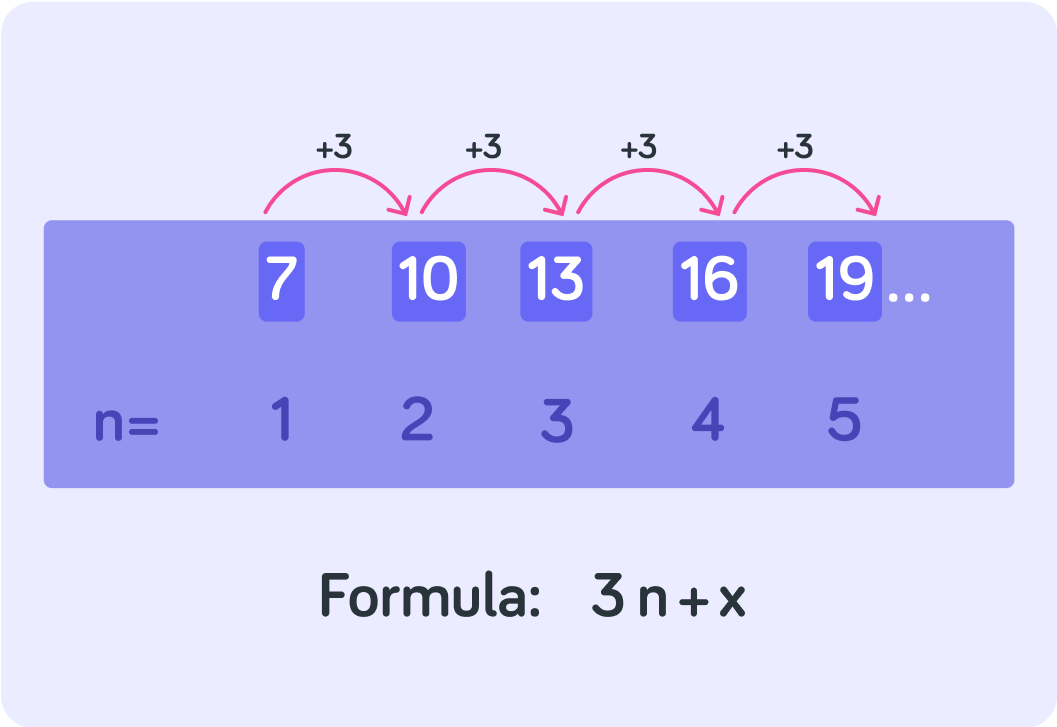
Now, what term value should the finished formula give you when $n=1$ ?

So you can substitute $1$ and $7$ into the formula like this $3 \times 1 + x = 7$ . What is $x$ ?

So now you have the formula. Try testing it. What do you get if you let $n=5$ ?

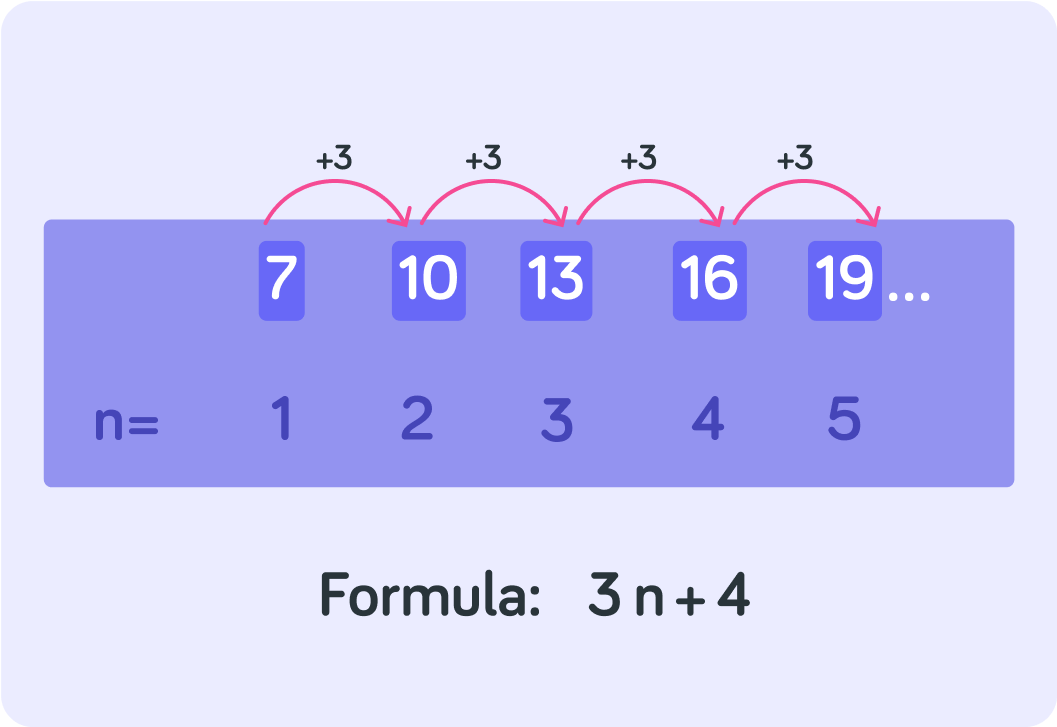
What would be the value of the 50th term in this sequence?

What is the difference between the each of the numbers in this sequence?

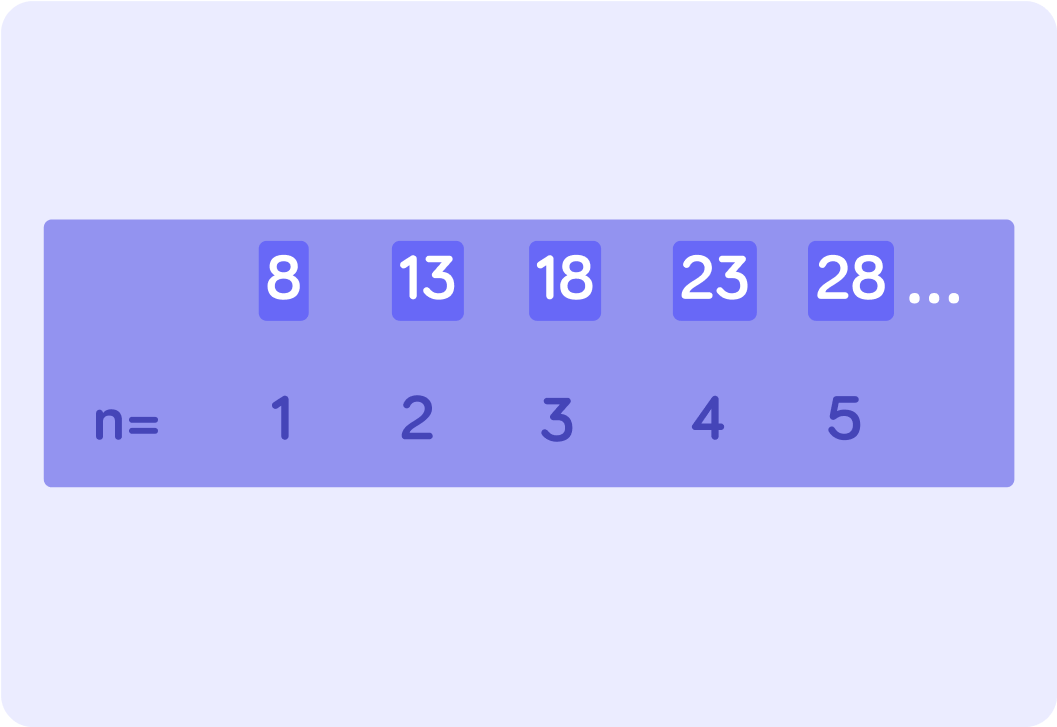
So what do you multiply $n$ by in the formula for this sequence?

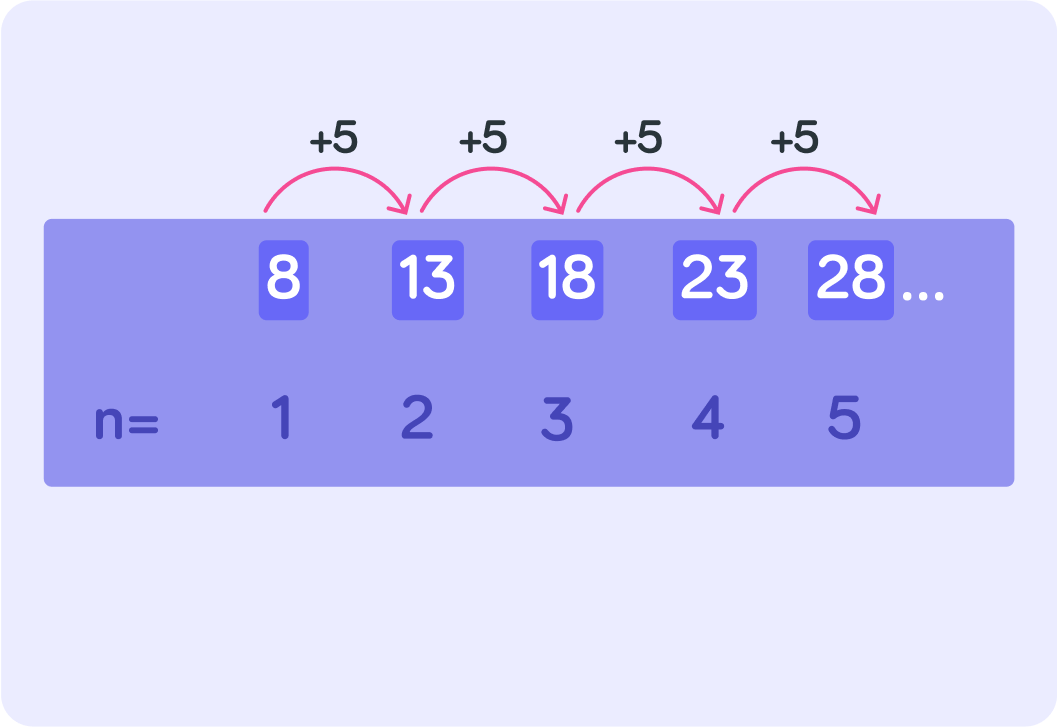
Now, let $n=1$ and work out what the $x$ in your formula should be.

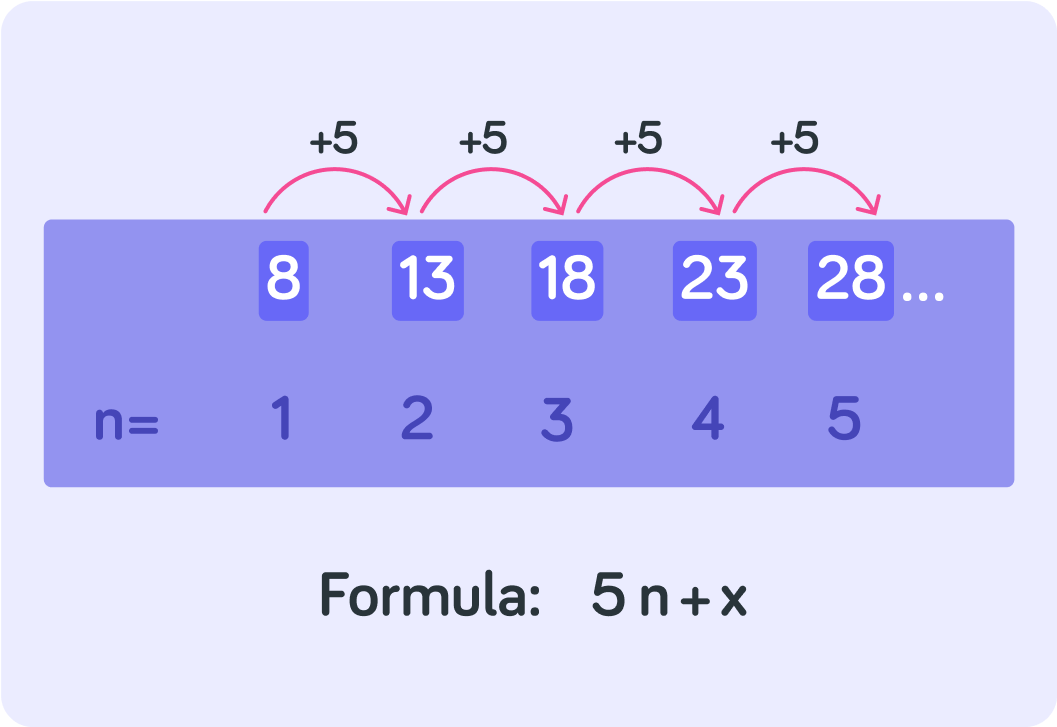
To recap! You found the formula like this

You worked out the difference between each of the numbers in the sequence, which gave you $5n$

When $n=1$ the formula should give you $8$ , so you worked out $x$ like this $5 \times 1 + x = 8$ , which means $x=3$

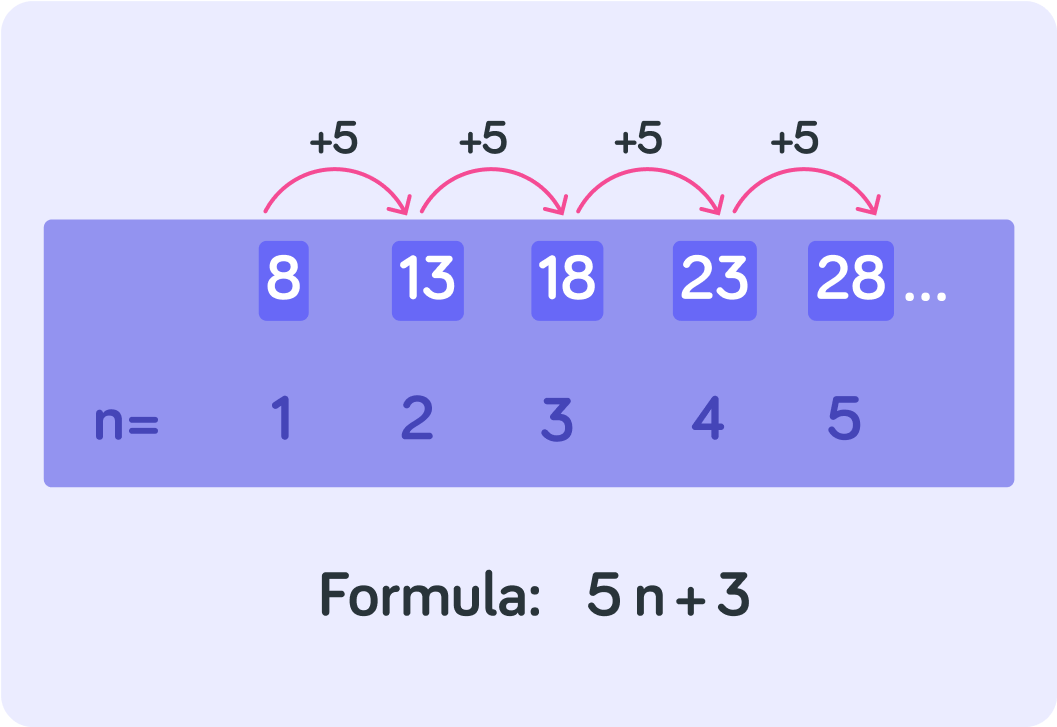
What is the 100th term in this sequence?

What is the 20th term in this sequence? $7 \space\space\space 11\space\space\space15\space\space\space19...$

Summary! This is an arithmetic sequence

There is a constant pattern in the terms in the sequence.

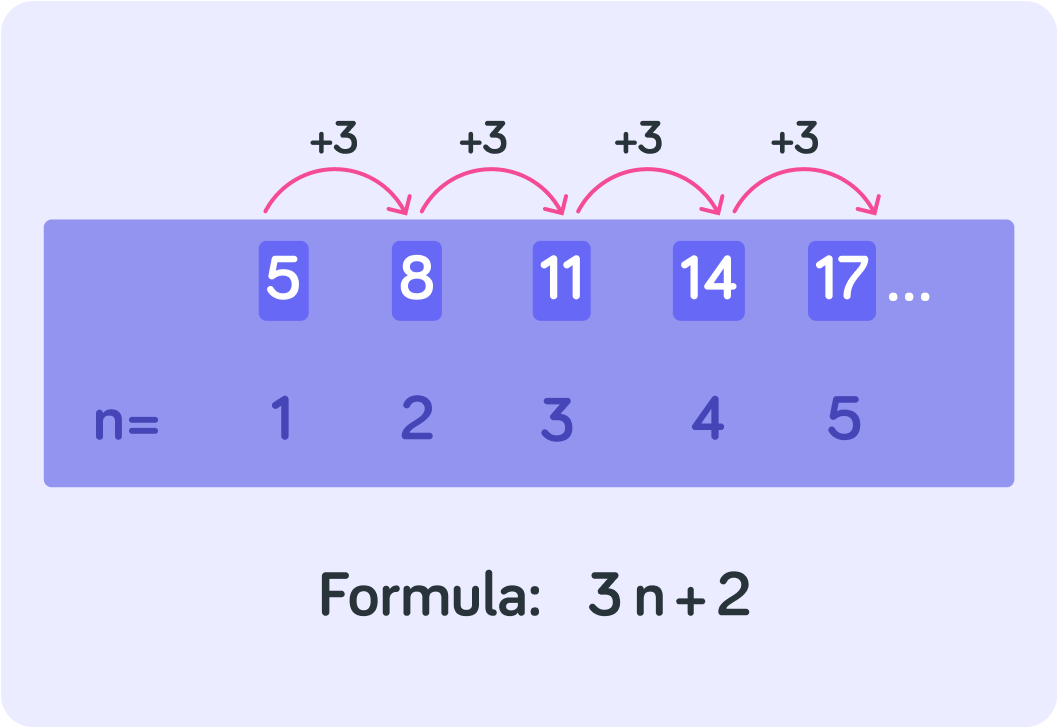
Each term can be labelled by a number $n$

You use that $n$ to work out a formula for the sequence, so you can find the value of any nth term in the sequence.

To work out the formula, you first find the pattern between the terms

Here they get $+3$ bigger every time $n$ gets 1 bigger, so the first part of your formula is $3n$

Then you find out what $x$ is by letting $n=1$

When $n=1$ , the formula should give $5$ , so you can work out $x$ like this $3 \times 1+x=5$ .

That means that $x=2$

You could now use this formula to work out any nth term

For example, the 10th term in this sequence would be $3 \times 10 +2 = 32$