Algebra

YOU ARE LEARNING:

Quadratic Sequences

Quadratic sequences don't have the same difference each time, but there is a pattern in the differences between consecutive numbers, which we can use to find the nth term.

Quadratic sequences are a type of sequence where there is a common difference between the differences between terms. This is sometimes called a second difference.

For example, let's consider the following sequence:

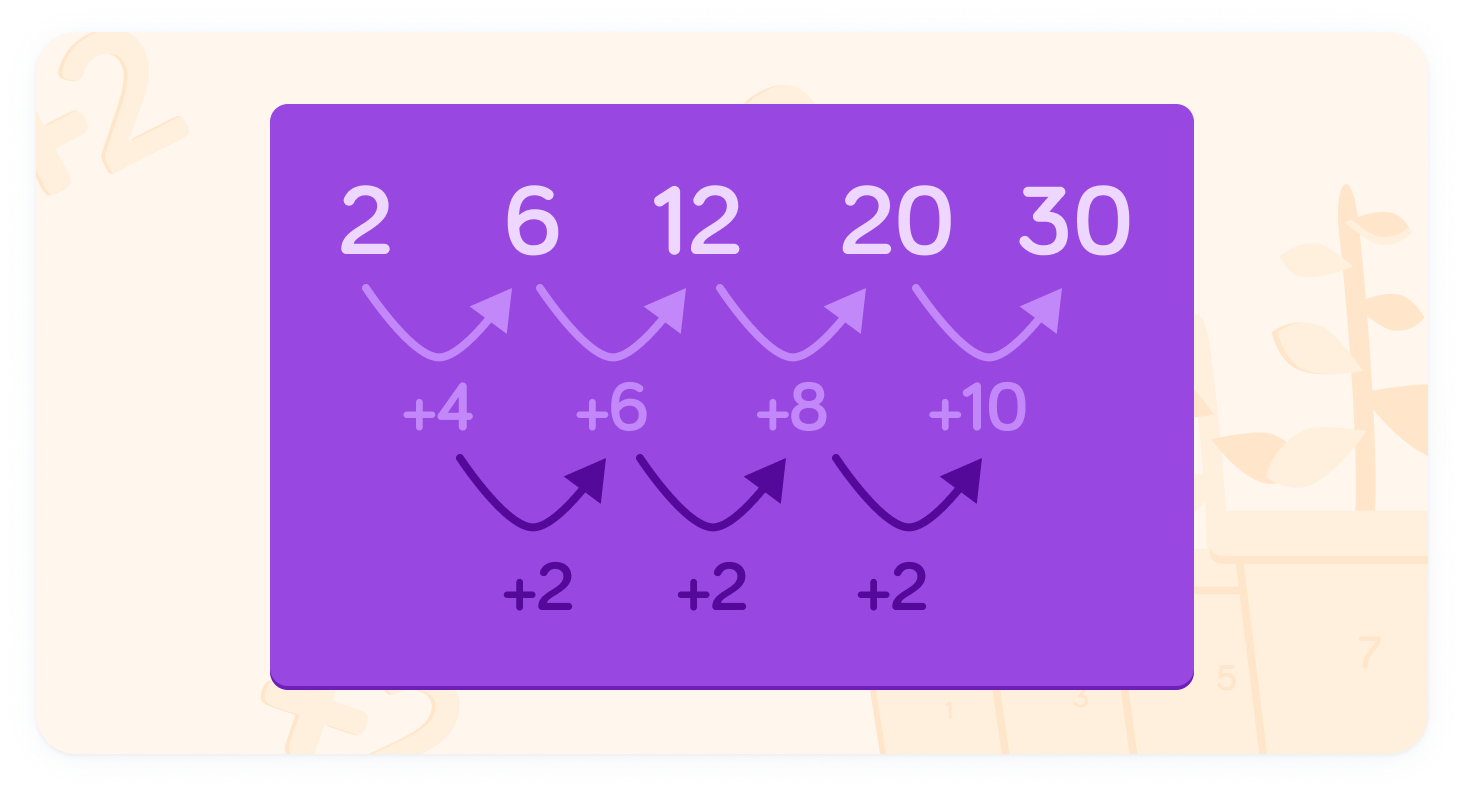
$2, 6, 12, 20, ....$

What is the difference between the first two terms?

How about the difference between the second and third terms?

And between the third and fourth terms?

What do you notice about this?

There is a common difference of $2$ between these differences. So the difference between each term increases by 2 for each new term.

This is called the second difference

The second difference of 2 indicates that this is a quadratic sequence.

What is the second difference of this sequence?

$3, 8, 15, 24...$

Let's continue with our sequence: $2, 6, 12, 20$

We know that the second difference is $2$

Therefore, each time there is a new term, the difference between it and the previous term increases by 2.

So what would the next term be?

The difference between the last two terms is $8$ . Since the second difference is $2$ , this means that the next term should be $8+2=10$ larger than the last term in the sequence.

What is the next term in the sequence?

Our sequence is now $2,6, 12, 20, 30$

We can keep adding terms to the end of the sequence, using the second difference of $2$ . The next term in the sequence would be $12$ larger than the last, since the difference between $20$ and $30$ is $10$ .

What is the next term in $2, 6, 12, 20, 30$ ?

The next term is $42$

Nice! 👍

What would be the next term in this sequence?

$3, 8, 15, 24$

The second difference is constant each time

Drawing a sequence out in this way can help you to identify a quadratic sequence.