Algebra

YOU ARE LEARNING:

Special Sequences: Geometric Sequences

Geometric sequences multiply each term by the same factor to produce the next term. We can use this idea to identify the nth term in a geometric sequence.

A geometric sequence is a sequence where each successive term is the result of multiplying the previous term by the same value, each time.

Let's look at an example

In this sequence, each term is $3 \times$ the previous term.

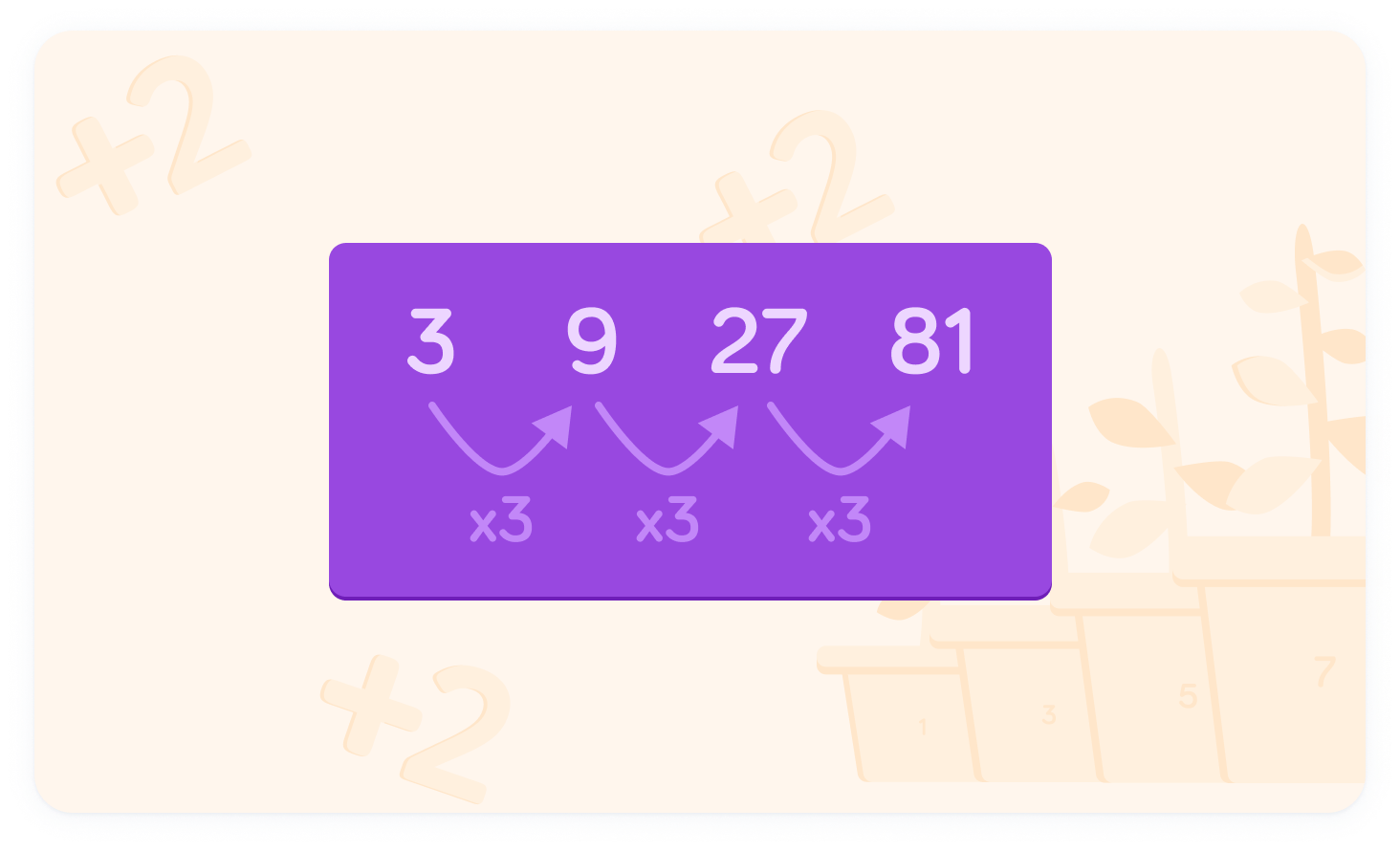
What would the next term in this sequence be?

The next term would be 243

Since each term is $3 \times$ the previous term, $3 \times 81=243$ .

Each of these terms are powers of 3

$3^1=3$ , $3^2=9$ , $3^3=27$ and $3^4=81$ . We can use this information to find the nth term for this sequence.

The nth term would be $3^n$

Remember, $n$ is the position in the sequence. Therefore, each number is a successive power of 3.

What is the next term in this sequence?

$2,4,8,16,32$

In a geometric sequence, the ratio between each pair of successive terms is the same.

Let's look at another geometric sequence: $100,50,25,12.5$

Look at the values to find the difference

Each value is half of the previous value in the sequence. Therefore, it is a geometric sequence because each value is multiplied by the same number to produce the next value in the sequence.

What would be the next value in the sequence?

So how would we find the nth term?

Each value is multiplied by $\dfrac{1}{2}$ in order to produce the next value in the sequence.

The nth term phrase starts with 100 (the first term)

To produce the second term in the sequence, we multiply $100 \times 0.5$ . To get to the third term in the sequence (25), we multiply by $0.5$ , then multiply by $0.5$ again. Multiplying by $0.5 \times 0.5$ is the same as $0.5^2$ .

The nth term is $a_n=100 \times 0.5^{n-1}$

To make the fourth term (12.5), we multiply 100 by $0.5 \times 0.5 \times 0.5$ , which is the same as $0.5^3$ . Therefore, we can see the pattern is to multiply the first value in the sequence by $0.5^{n-1}$ , so the nth term is $100\times0.5^{n-1}$ .

The nth term is $100 \times 0.5^{n-1}$ . What is the 8th term to 3 dp?