Algebra

YOU ARE LEARNING:

Arithmetic Sequences 2

Arithmetic Sequences 2

Arithmetic progressions are sequences of numbers that can be generated with an algebraic formula, which we can use to find the nth term.

An arithmetic progression is a sequence of numbers that can be generated with an algebraic formula.

A sequence, however, can be based on a logical rule such as 'the odd prime numbers'.

This is a sequence of numbers

The difference between each of the numbers is 3.

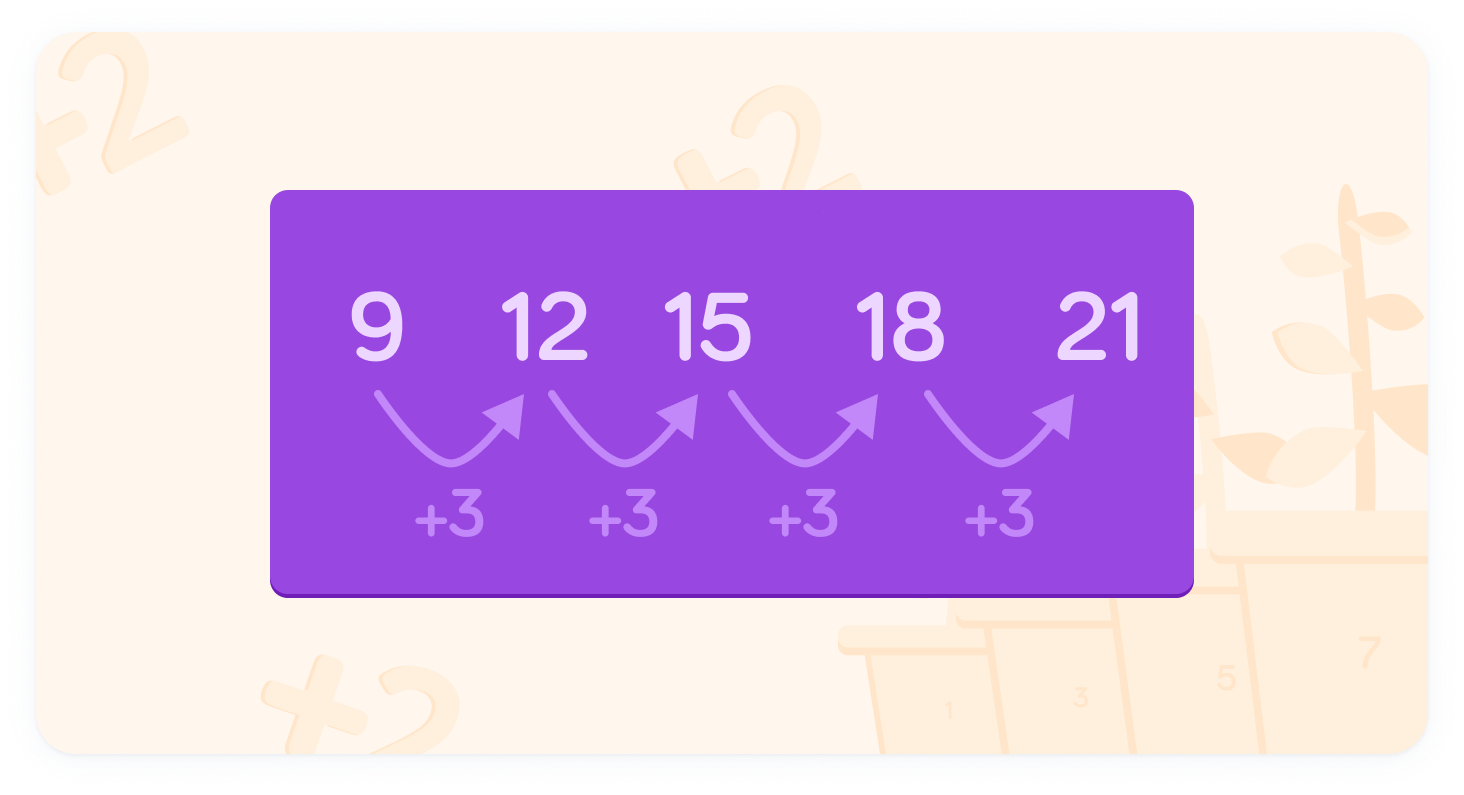
We can describe the sequence using algebra

The first term is $a$ , while the difference between terms is $d$ . We can assign each term a value based on its distance from $a$ .

Notice that $d$ is one less than the position

For the second term, the value is $a+d$ . For the third term, the value is $a+2d$ . We can generalise this - the nth term is $a+(n-1)d$ .

$a+(n-1)d$ gives us the nth term

We can use this formula to find any term in the sequence.

If $a+(n-1)d$ , what is the 38th term?

The 38th term is $120$

We can substitute $a=9$ and $d=3$ into the formula to find $3+(38-1)\times 3=120$

For the following sequence, identify the value of $a$ and $d$ :

$8, 14, 20, 26, 32 …$

For the following sequence, identify the value of $a$ and $d$

$14, 10, 6, 2, -2…$

As well as using the formula for the nth term of an arithmetic sequence, you will have to use the sum formula. This helps us to find the sum of consecutive terms in the sequence.

This is the sum formula

$S_n$ is shorthand for 'the sum of the sequence', while $a$ is the first term in the sequence and $d$ is the difference between each term.

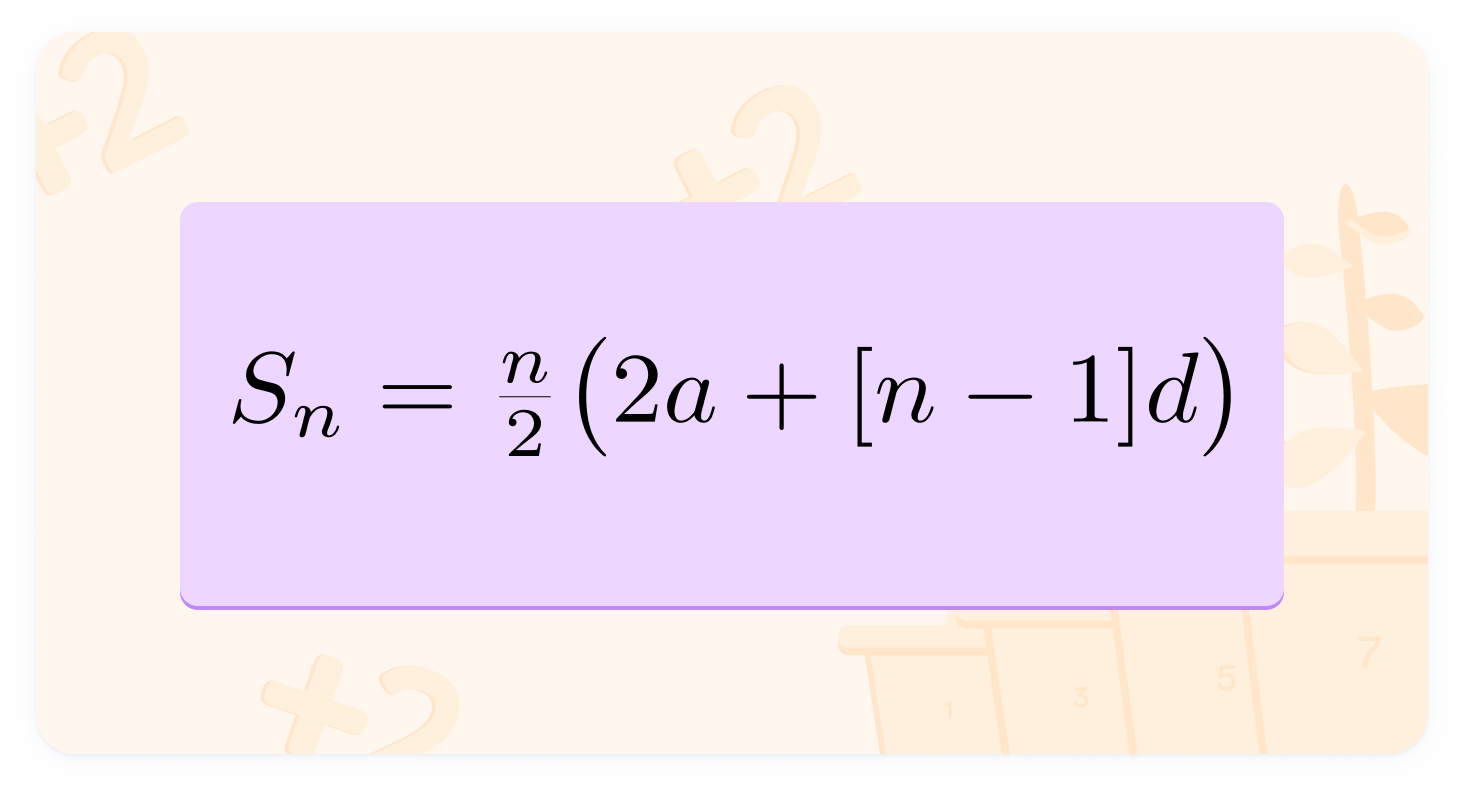
This is another variant of the Sum Formula

Using this one relies on knowing the LAST term in the sequence.

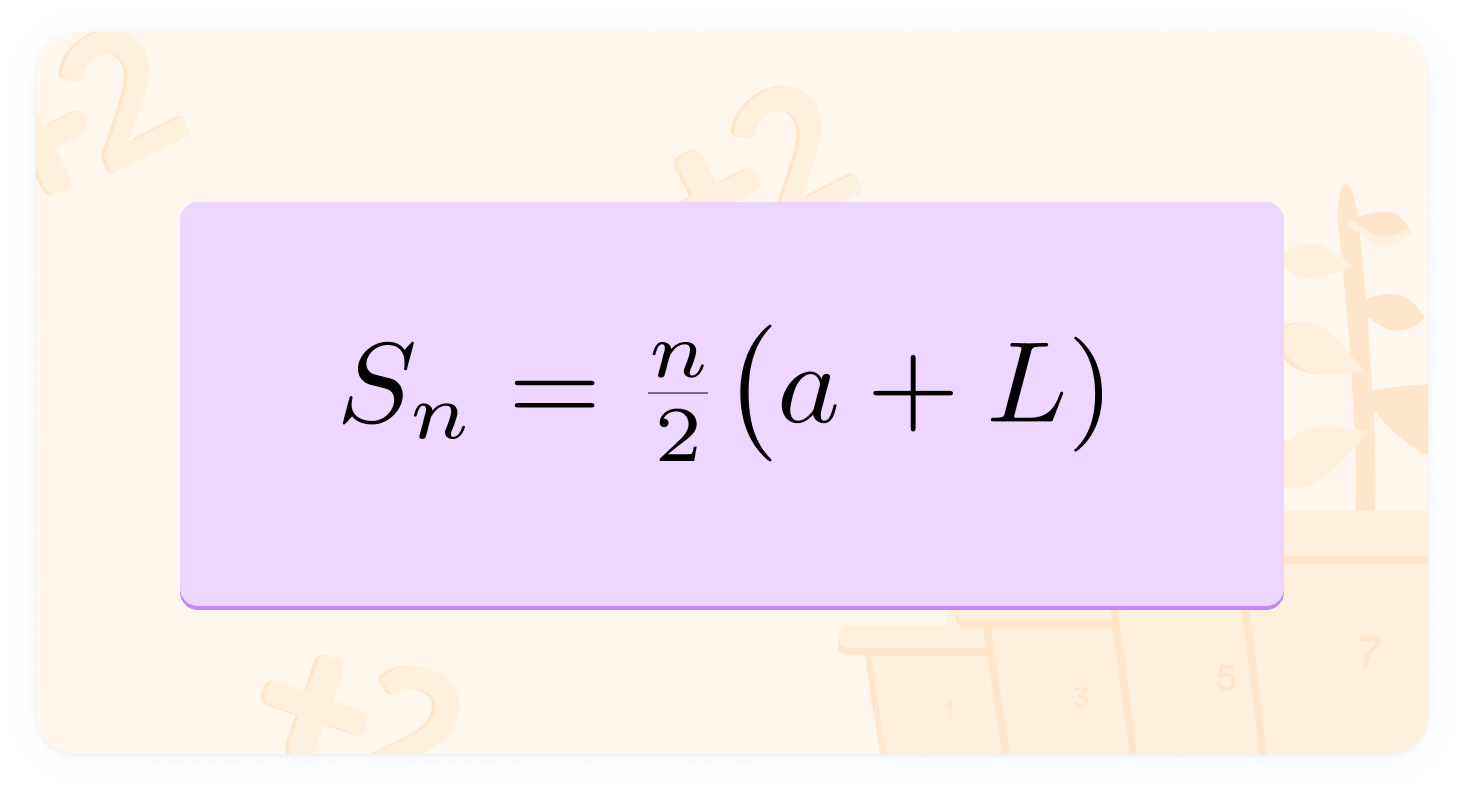
Let's try an example. For example, what is the sum of the first 10 terms of the sequence that begins: $4,10,16...$ ?

What is the first term $a$ ?

What is the common difference?

We can see that $n=10$ in the question

So, we have each of the values we need for the sum formula. $a=4$ , $d=6$ and $n=10$ .

Let's put these values into the equation

$S_n = \dfrac{n}{2}\big(2a + [n-1]d \big) \rightarrow S_{10} = \dfrac{10}{2}\big(2\times4 + [10-1]6 \big)$

Now we can solve the equation

$S_{10} = \dfrac{10}{2}\big(2\times4 + [10-1]6 \big) \rightarrow S_{10}=5(8+9\times6)$

What is the value of $S_{10}$ ?

Awesome! 😎

The sum of the first 10 numbers is $310$