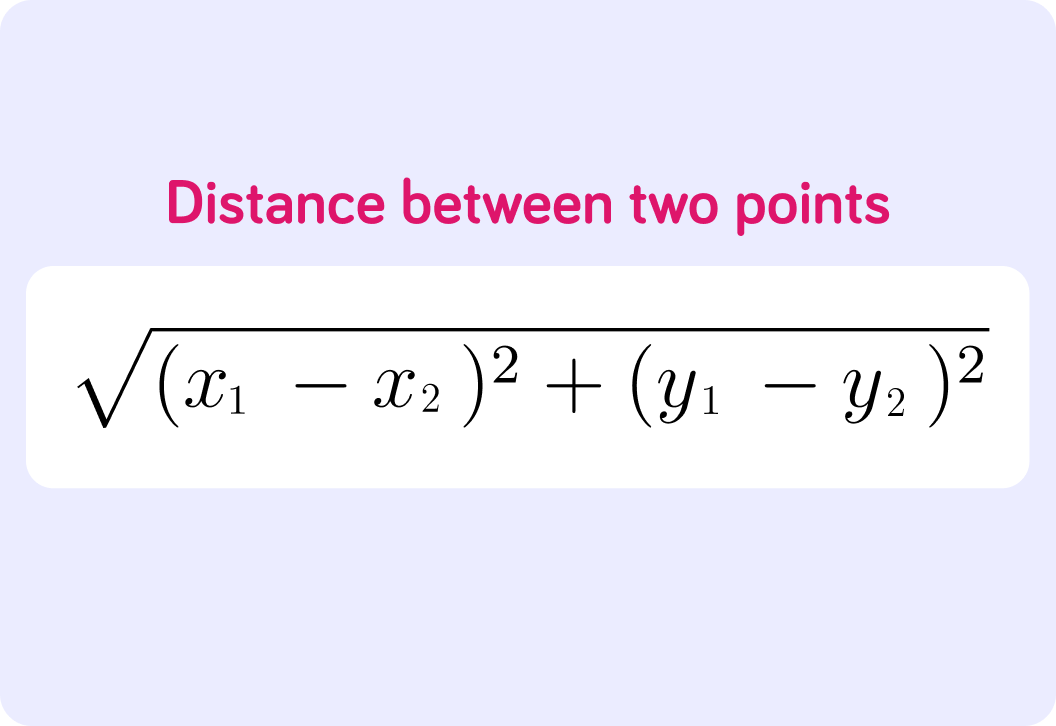1

Cartesian coordinates (or just coordinates) are a pair of numbers that define a point in the plane (as shown). What is the right way to write these coordinates?

1

The axes divide the plane into 4 quadrants

Each quadrant is numbered as shown in the diagram.

2

The horizontal or $x$ axis is first and moving right is positive. The vertical or $y$ axis is second and moving up is positive. What type of coordinate sits in the 3rd quadrant?

3

We can use the same principle to work out the other quadrants.

Each quadrant has a unique combination of positive and negative values for the coordinates.

4

Where the axes cross, where you see a $0$ , is called the origin. What are the coordinates of the origin?

1

What is the coordinate of the point $A$ shown here?

2

What is the coordinate of point $B$ ?

1

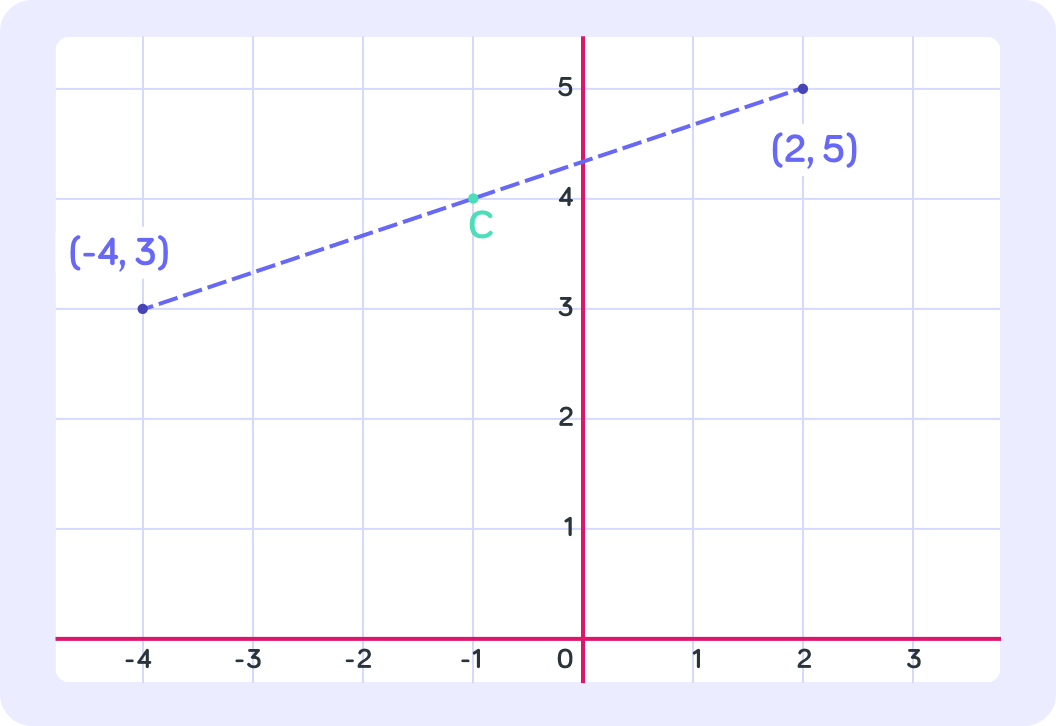
Point $C$ is the mid-point between points $A=(2,5)$ and $B=(-4,3)$ .

We can see it on the graph, but how can we calculate the coordinates?

2

To find the mid-point between two numbers we add them together and divide by $2$ . Based on that, what will the $x$ coordinate of the mid-point be?

3

Using the same process, what is the $y$ coordinate of the mid-point?

4

Putting the two together our mid-point has coordinates $(-1,4)$ .

We can see this matches what we have on the graph.

5

This gives us a formula for finding the mid-point between two points.

For any two points $(x_1,y_1)$ and $(x_2,y_2)$ we can use this formula to find the mid-point between them.

1

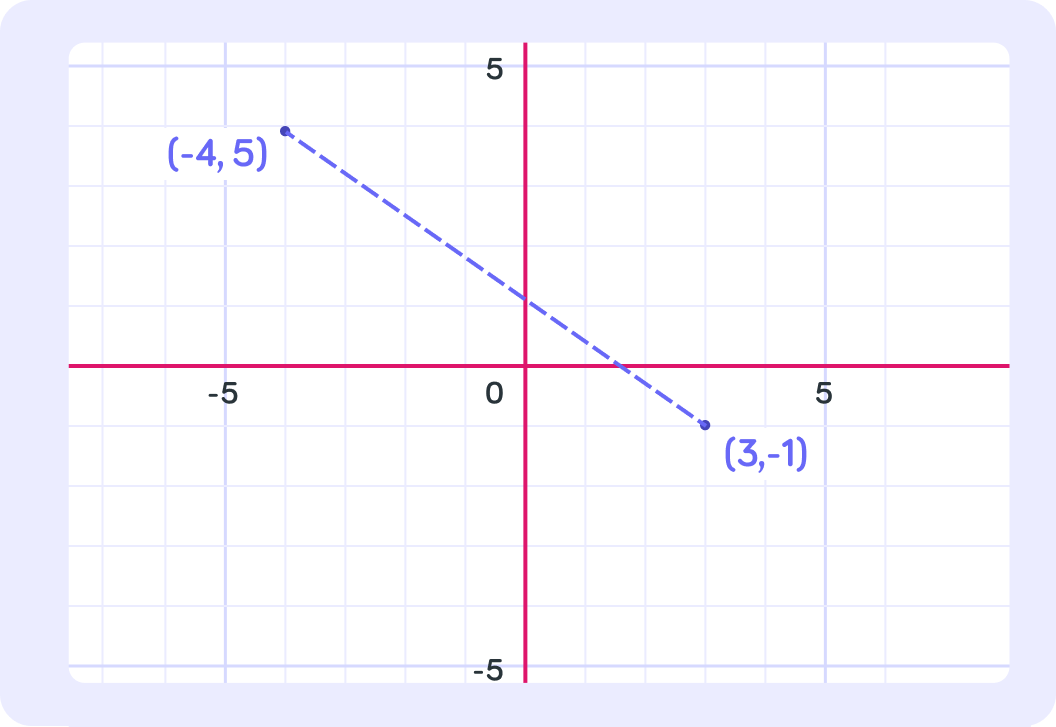
What is the mid-point between the two points $(-4,5)$ and $(3,-1)$ ?

1

We may also want to find the distance between two points.

By completing a right angled triangle, we can find this distance.

2

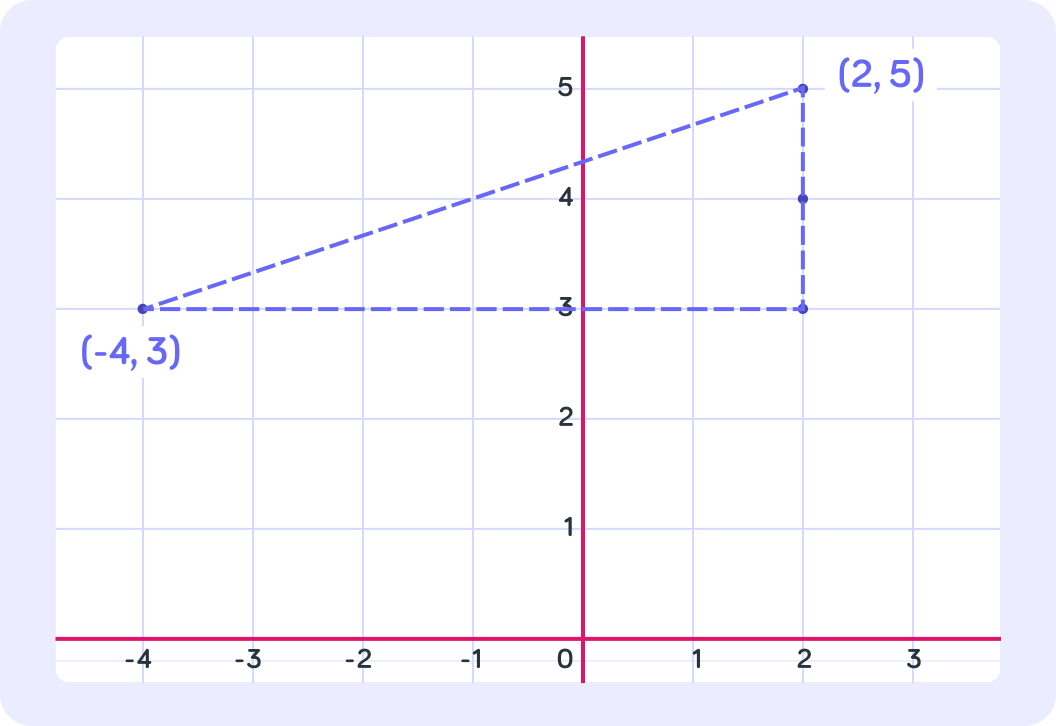
What is the horizontal distance in this triangle?

3

What is the vertical distance in this triangle?

4

Now we have a right angled triangle and we know the distance along two sides.

We can use Pythagoras' Theorem to find the third side. It is $a^2 + b^2 = c^2$

5

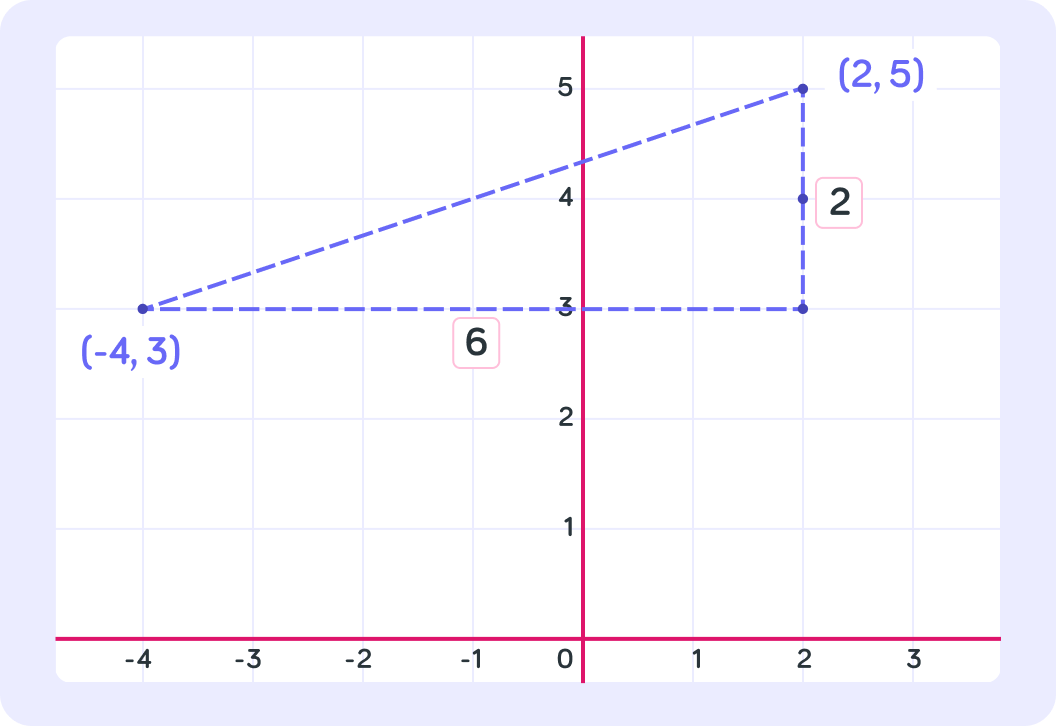
Using Pythagoras' Theorem ( $a^2 + b^2 = c^2$ ), what is the distance between the two points? Give your answer to one decimal place.

6

We can summarise these steps in one formula.

For any two points $(x_1,y_1)$ and $(x_2,y_2)$ we can use this formula to find the distance between them.

1

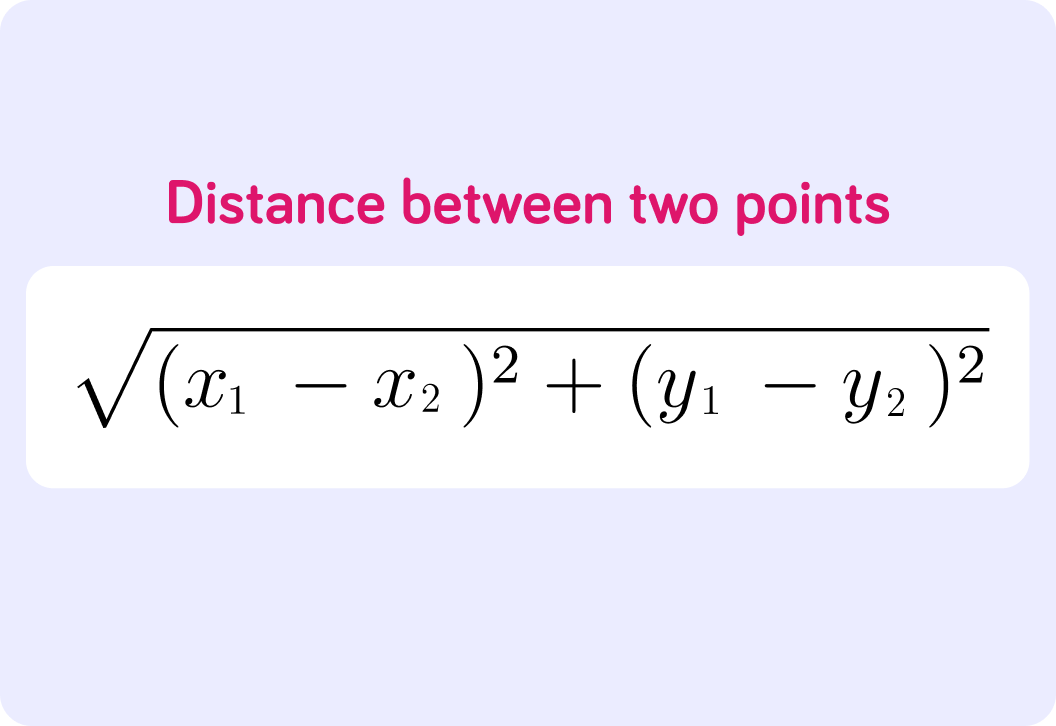
What is the distance between the points $(-4,5)$ and $(3,-1)$ ? Give your answer to 1 decimal place

1

In summary, Cartesian coordinates show us where a point is in the plane.

Cartesian coordinates are written $(x,y)$ .

2

The point where the axes cross is called the origin.

The coordinates are the origin are $(0,0)$ .

3

There are four quadrants in the plane.

Each quadrant has a unique combination of positive and negative values for the coordinates.

4

The mid-point between two lines can be found using this formula.

The mid-point between $(-8,6)$ and $(3,4)$ is $(\frac{-8+3}{2},\frac{6+4}{2})=(-2.5,5)$ .

5

We can find the distance between two points using Pythagoras's Theorem.

The distance between $(-8,6)$ and $(3,4)$ is $\sqrt{(-8-3)^2+(6-4)^2}=\sqrt{121+4}=11.2$ to one decimal place. Distance between two points $=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

Coordinates

Coordinates