Graphs

YOU ARE LEARNING:

Straight Line Graphs 2

Straight Line Graphs 2

We can find the equation of a straight line by finding the gradient and the y-intercept.

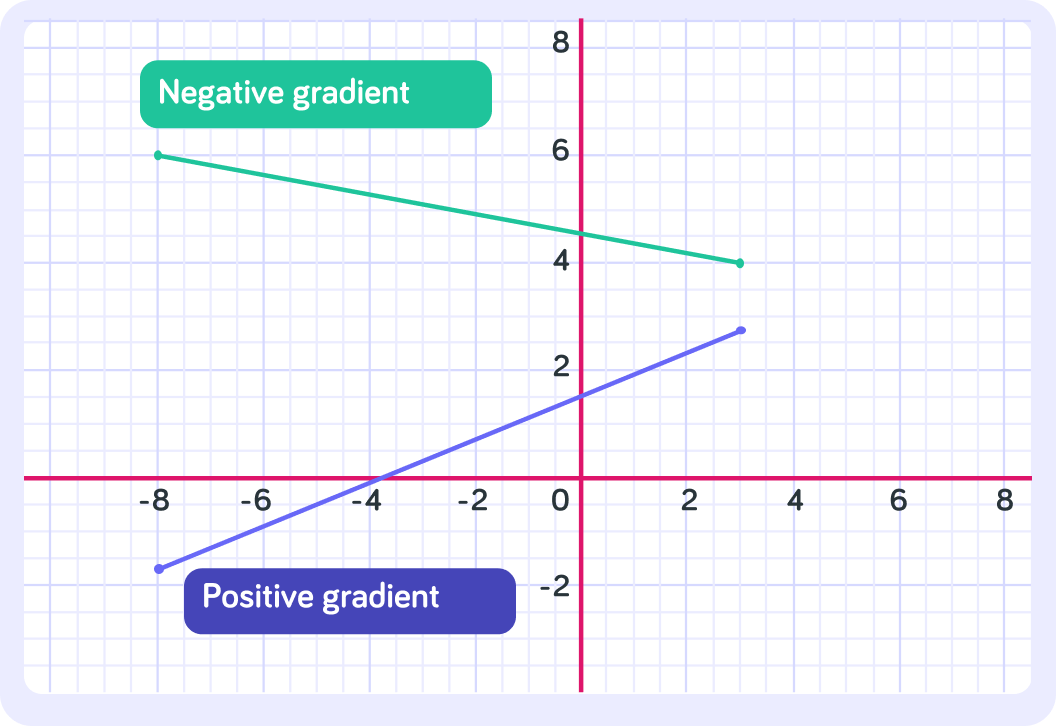
The gradient tells us a couple of things about a line - what are they?

The direction of the slope is determined by the sign of the gradient.

A positive gradient rises from left to right. A negative gradient descends from left to right.

We can calculate the gradient of a straight line if we know two points on that line.

This is the line that passes through the points $(2,8)$ and $(0,2)$ .

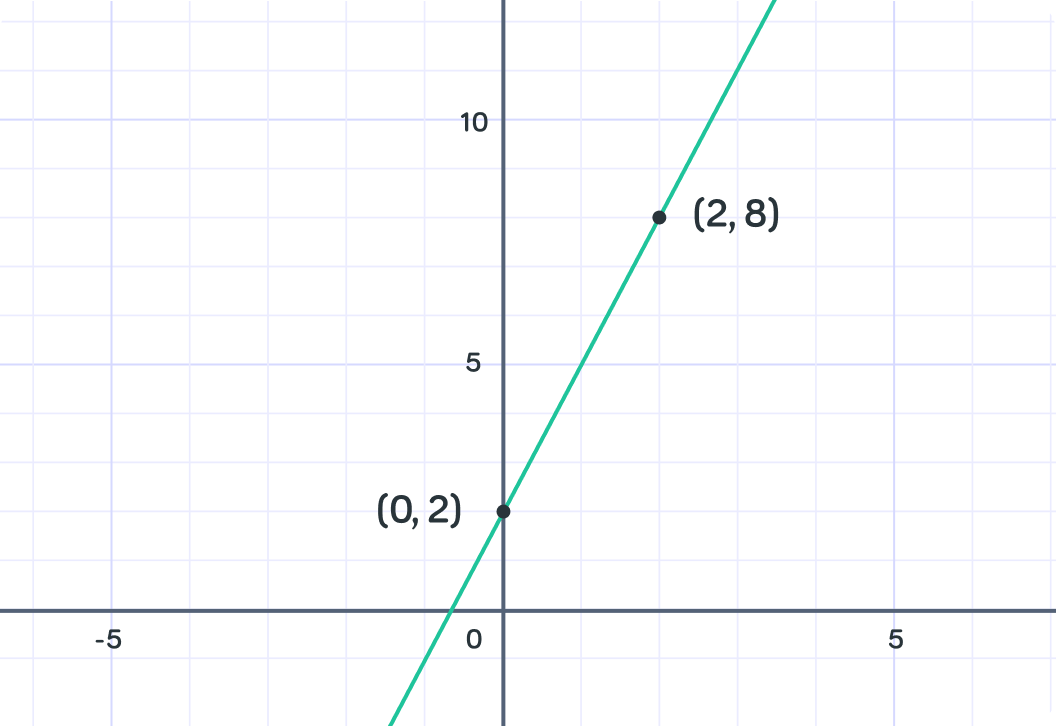
We need to find the difference in the $y$ coordinates and divide by the difference in the $x$ coordinates.

This is also known as $\frac{rise}{run}$ .

What is the difference between the $y$ coordinates?

What is the difference in the $x$ coordinates?

We know that $m=\frac{6}{2}$ so what is the gradient of this line?

It doesn't matter which point we use first but we must be consistent with the two coordinates.

We used $\frac{8-2}{2-0}=\frac{6}{2}=3$ We could have used the points the other way round $\frac{2-6}{0-2}=\frac{-6}{-2}=3$ .

We can use the formula to find the gradient of the line.

The gradient of the line is normally shown as $m$ .

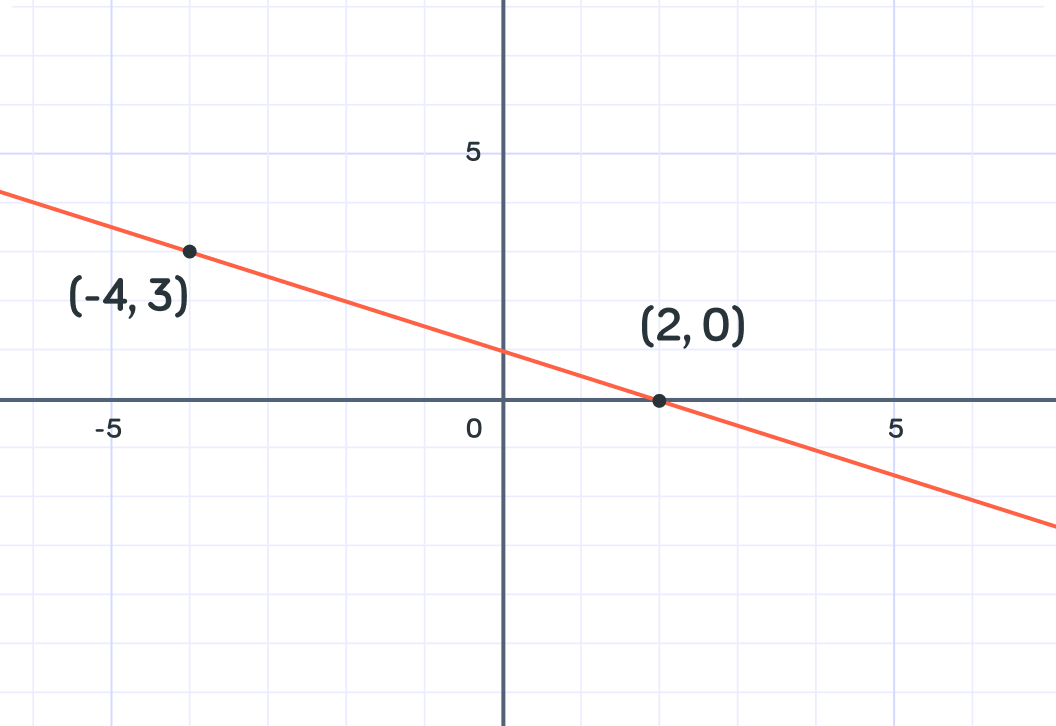
What is the gradient of the line which passes through the points $(-4,3)$ and $(2,0)$ .

The standard form of the equation of a straight line is $y=mx+c$ where $m$ is the gradient and $c$ is the $y$ intercept. What is the $y$ intercept on this straight line graph?

This is the same line whose gradient we found to be $-0.5$ . Now we know the $y$ intercept is $1$ , what is the equation of the line.

What is the gradient of the line with equation $y-3x=5$ ?

Now we know that the straight line has standard equation $y=mx+c$

we can find the equation of a line given the gradient and one point.

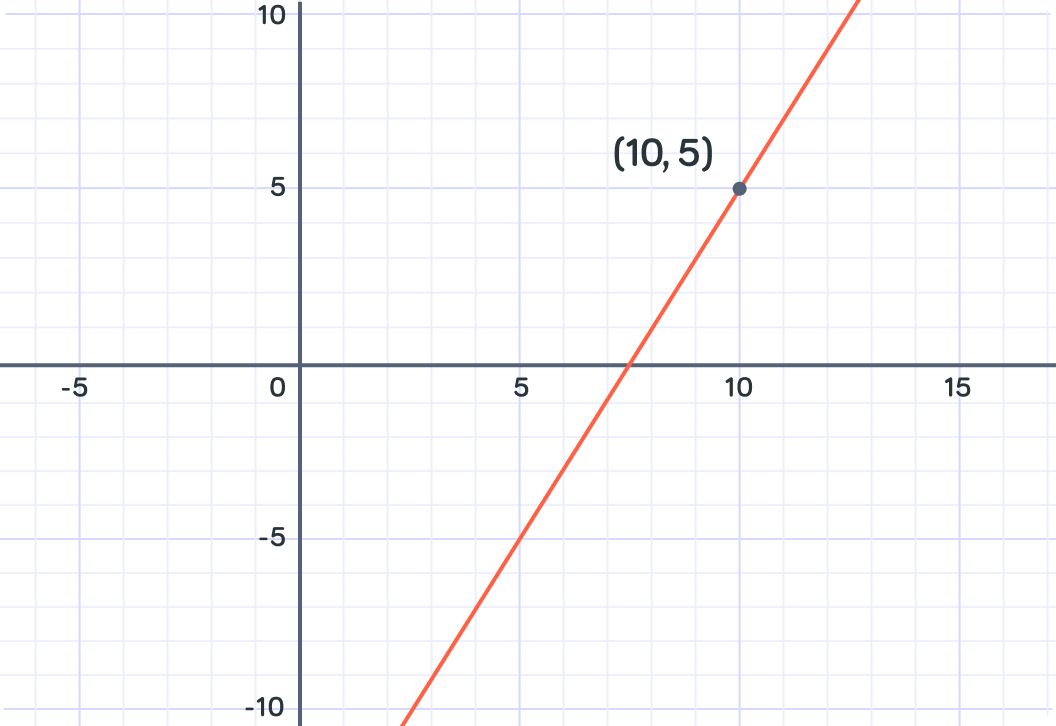
This line passes through the point $(10,5)$ and has gradient $2$ . The first step is to take the standard form of the equation and put in the gradient. Select the correct option.

We now have part of our equation $y=2x+c$ . We can use the point coordinates to work out $c$ by substituting into our equation, $5=2\times 10+c$ . What is $c$ ?

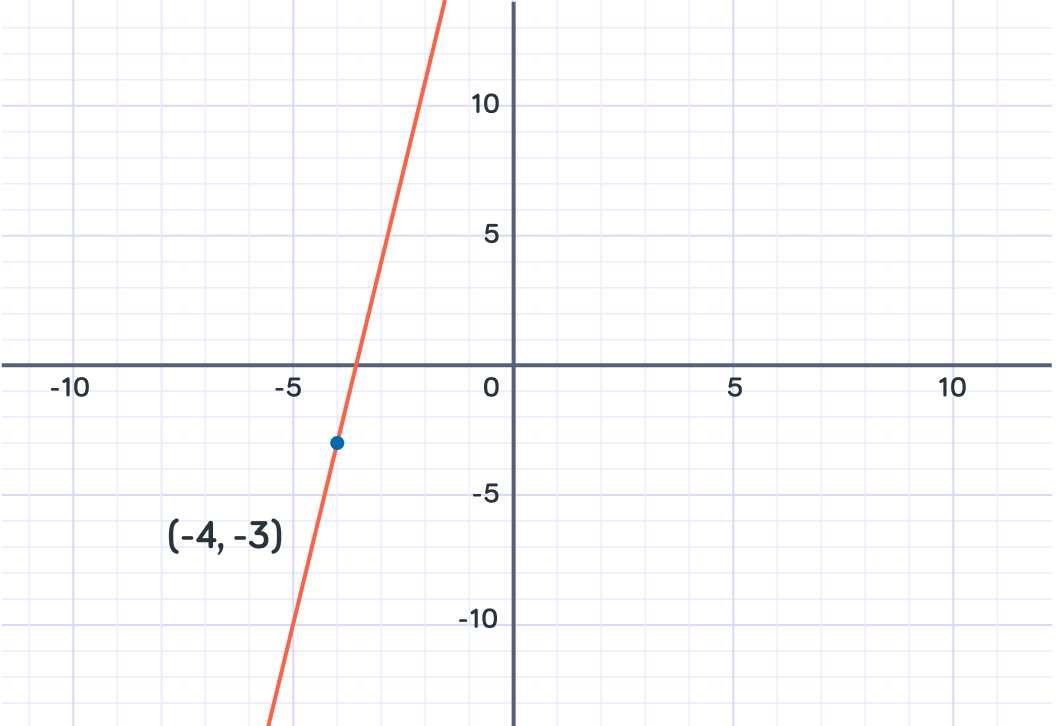
What is the equation of the line with gradient $7$ and passes through the point $(-4,-3)$ ?

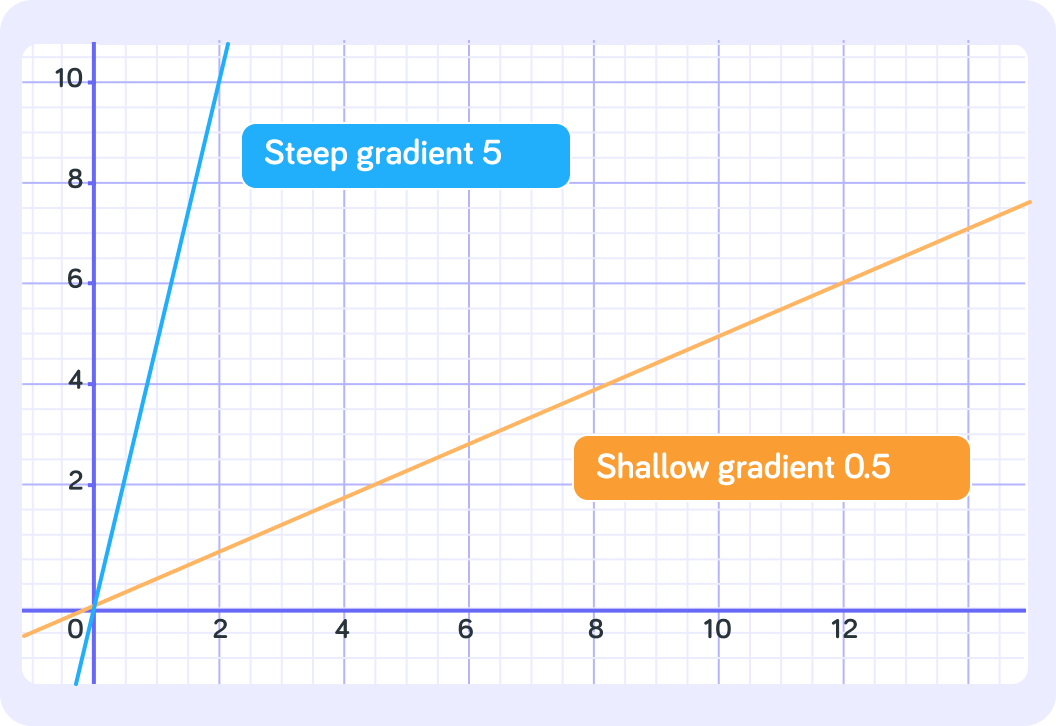
Summary! The gradient of the line is denoted by a number.

A positive gradient rises from left to right. A negative gradient descends from left to right.

The larger the number in the gradient, the steeper the line.

A gradient of $0.5$ is quite shallow. A gradient of $5$ is steep.

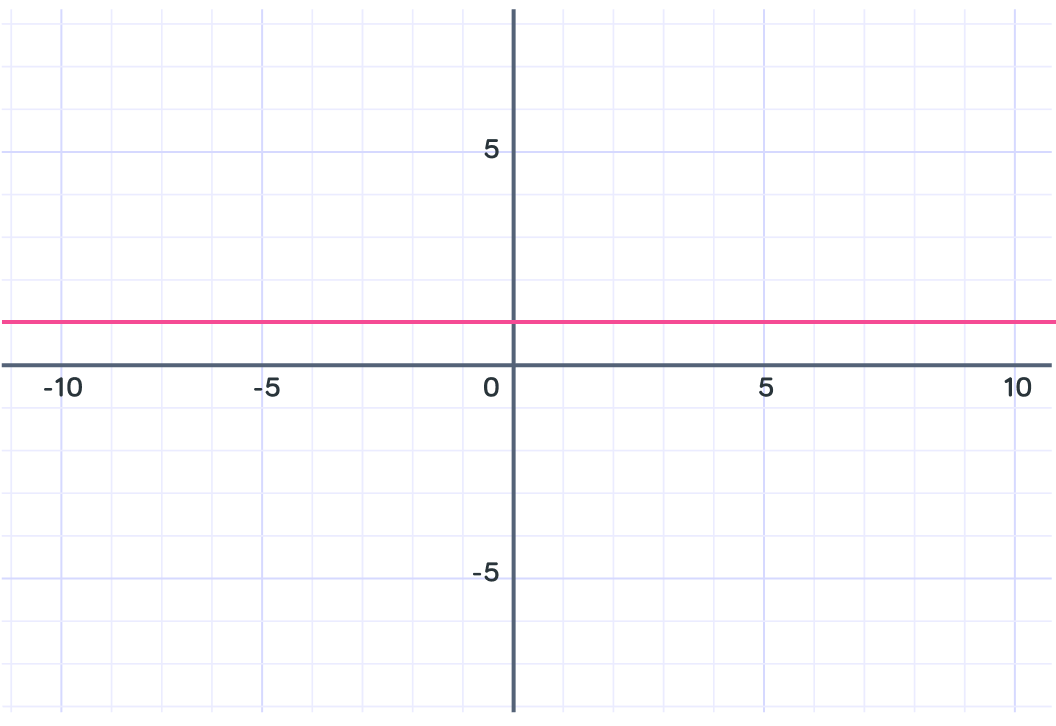
A horizontal line has a gradient of $0$ .

The line does not go up or down.

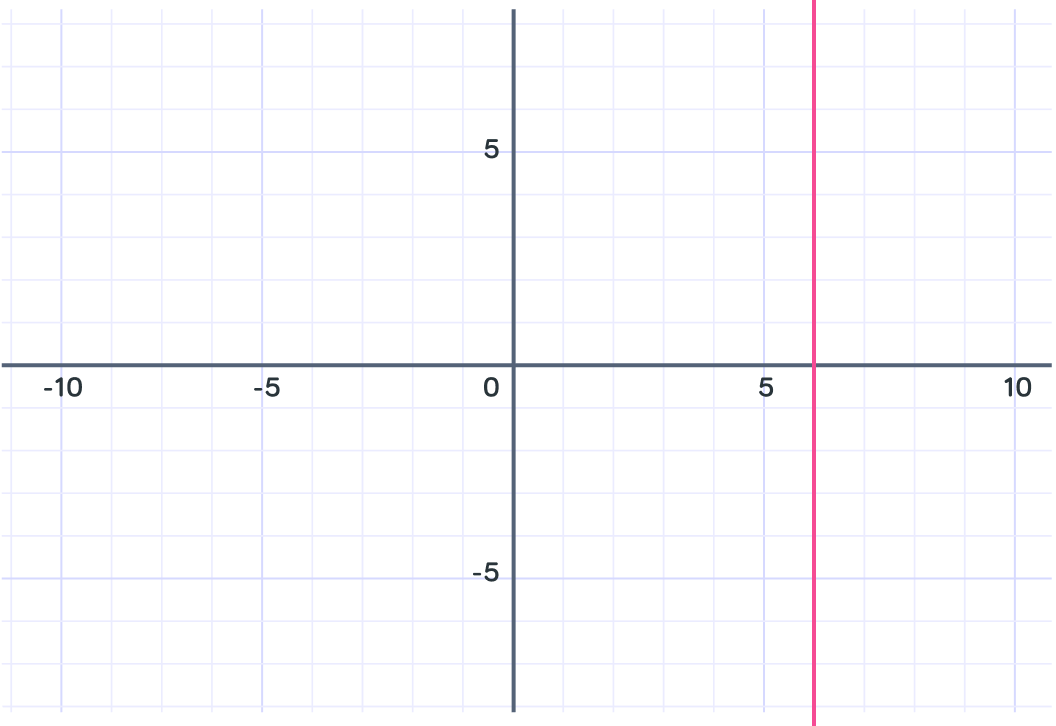
A vertical line has an infinite gradient.

The line only goes up.

We can calculate the gradient of a line if we know two points on that line.

The gradient of a line is normally shown by the letter $m$ .

The standard equation of a straight line is $y=mx+c$

Here, $m$ is the gradient and $c$ is the $y$ intercept.

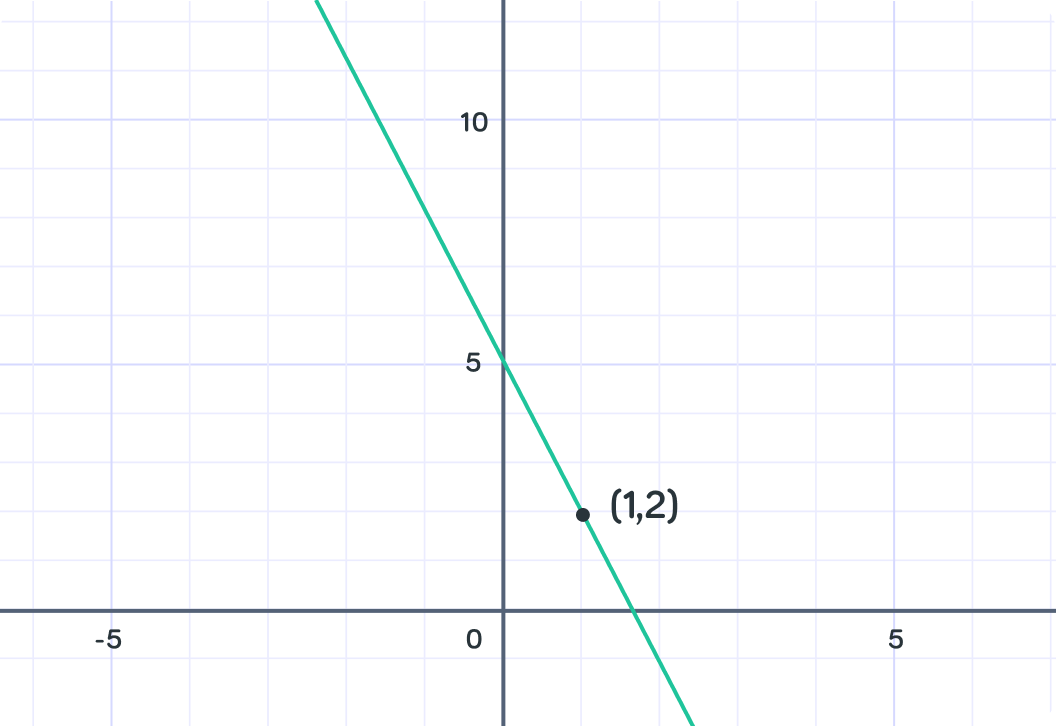
We can find the equation of a line with the gradient and one point here that is $-3$ and $(1,2)$ .

We start the equation $y=-3x+c$ . Substitute the point, $2=-3\times 1+c$ and $c=5$ so the full equation is $y=-3x+5$ .

Sometimes the equation of a straight line needs to be rearranged to put it into standard form.

The line with equation $y-x=5$ . Rearrange to leave $y$ on the left hand side, $y=x-5$ and this is standard form. The gradient is $1$ and the $y$ intercept is $-5$ .