Number

YOU ARE LEARNING:

Dividing Fractions

When you divide fractions, you basically do the opposite of when you multiply them.

Division is the opposite of ______________.

This formula shows how you multiply fractions

When you divide fractions, you do the opposite of when you multiply fractions.

What does that mean?

When you divide two fractions, what do you do to one of the fractions?

Also, what has the division sign turned into?

So how do you divide two fractions?

You flip one of the fractions and change the division sign to a multiplication sign.

What does the second fraction in this problem become when you flip it?

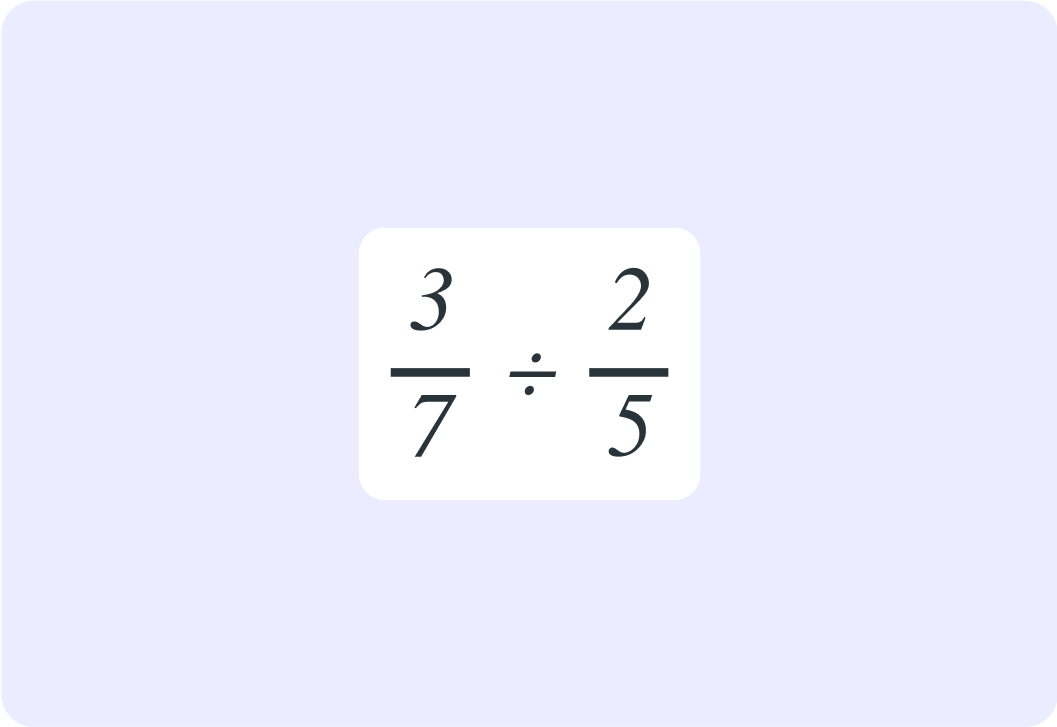
Now that you have flipped one of the fractions, you have to remember to also change the division sign into a _________________ sign.

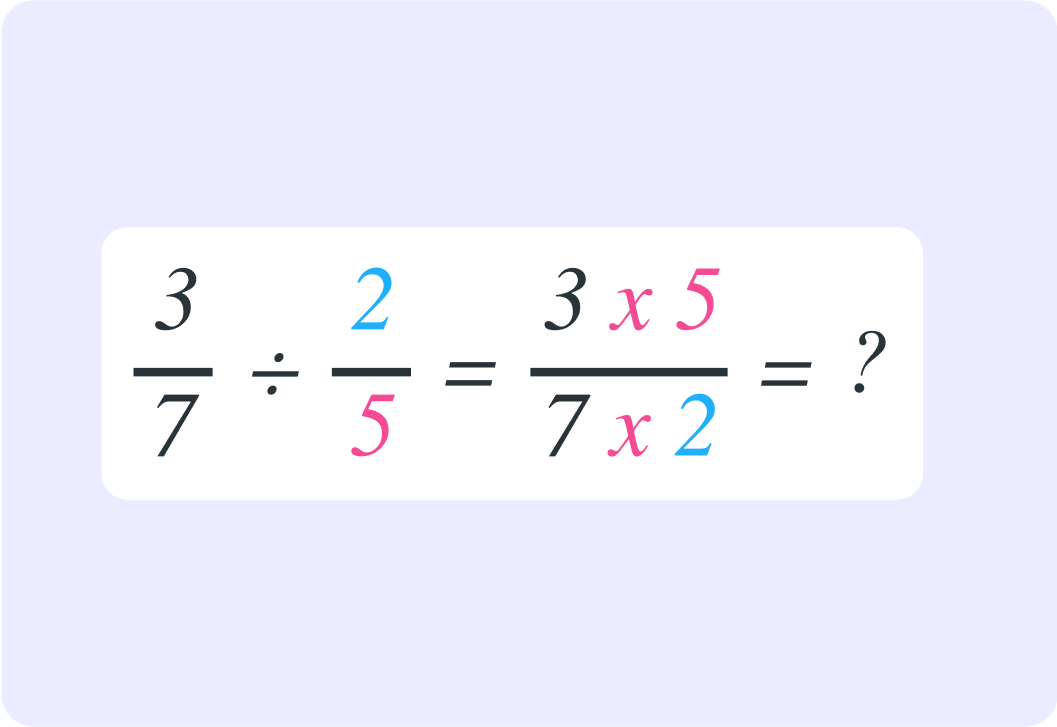
So what is the result here? Give your answer as a fraction.

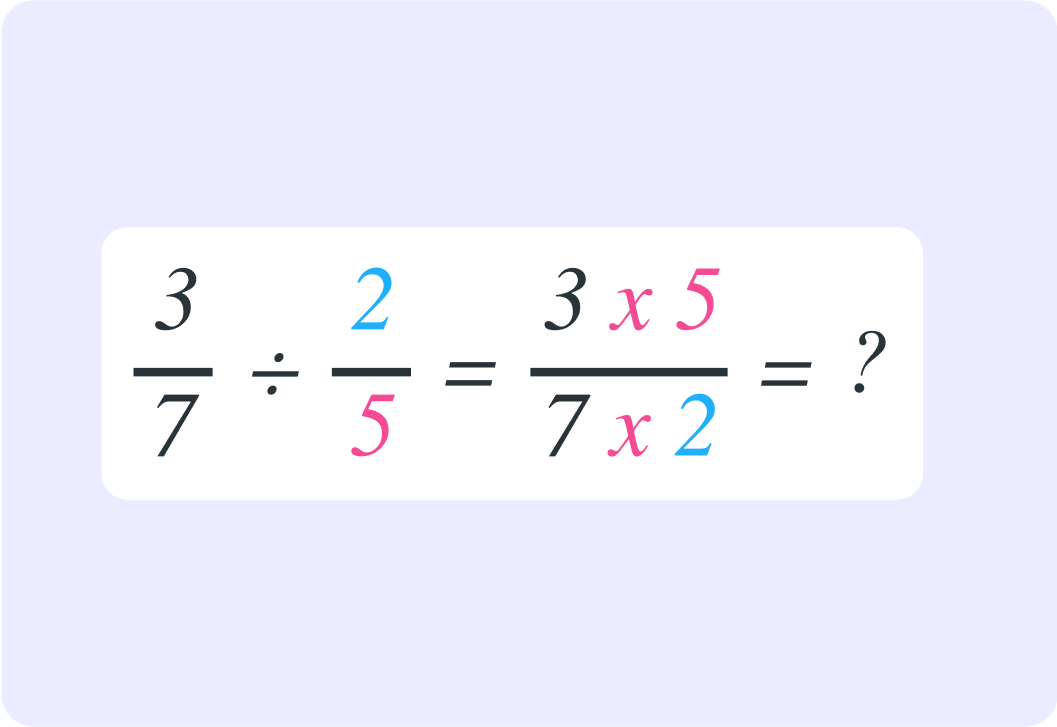
There you have it!

$\frac{3}{7} \div \frac{2}{5} = \frac{15}{14}$

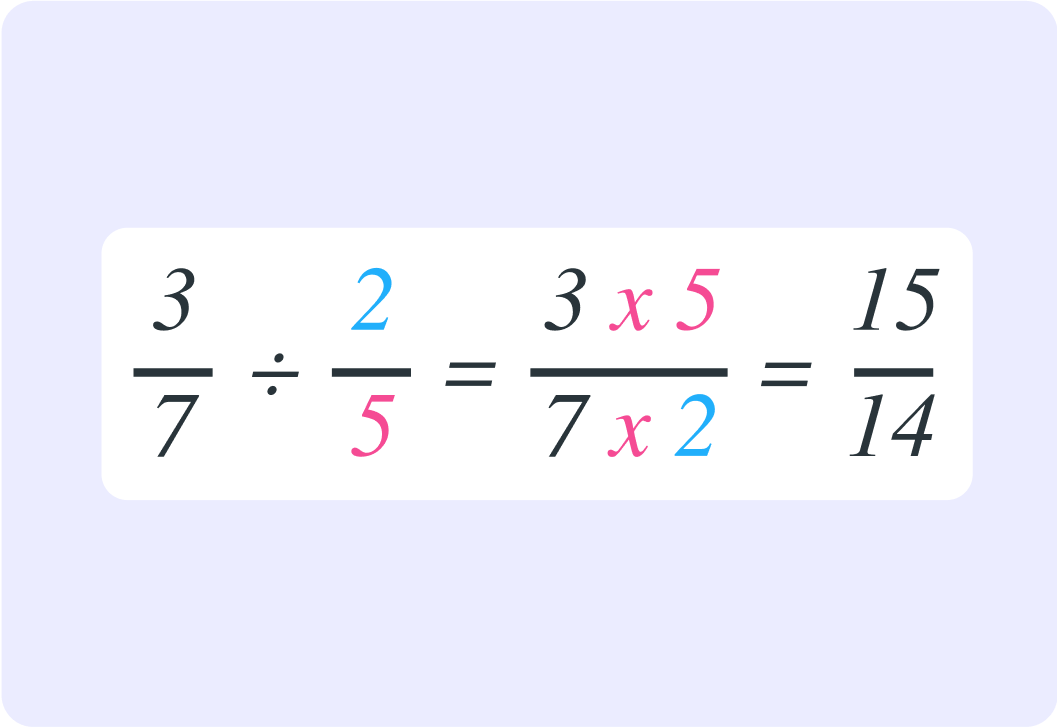
Work out $\frac{4}{9} \div \frac{3}{8}$ . Give your answer as a fraction.

Work out $\frac{4}{20} \div \frac{5}{10}$ . Give your answer as a fully simplified fraction.

When you divide fractions, you do the opposite to when you multiply them

You flip one of the fractions and change the division sign to a multiplication sign

For example

$\frac{4}{3} \div \frac{5}{3} = \frac{4 \times 3}{3 \times 5}=\frac{12}{15}$