Number

YOU ARE LEARNING:

Simplifying Fractions

Simplifying Fractions

You can make fractions easier to read by simplifying them.

Pizza A was divided into four slices and two are left. What is this as a fraction?

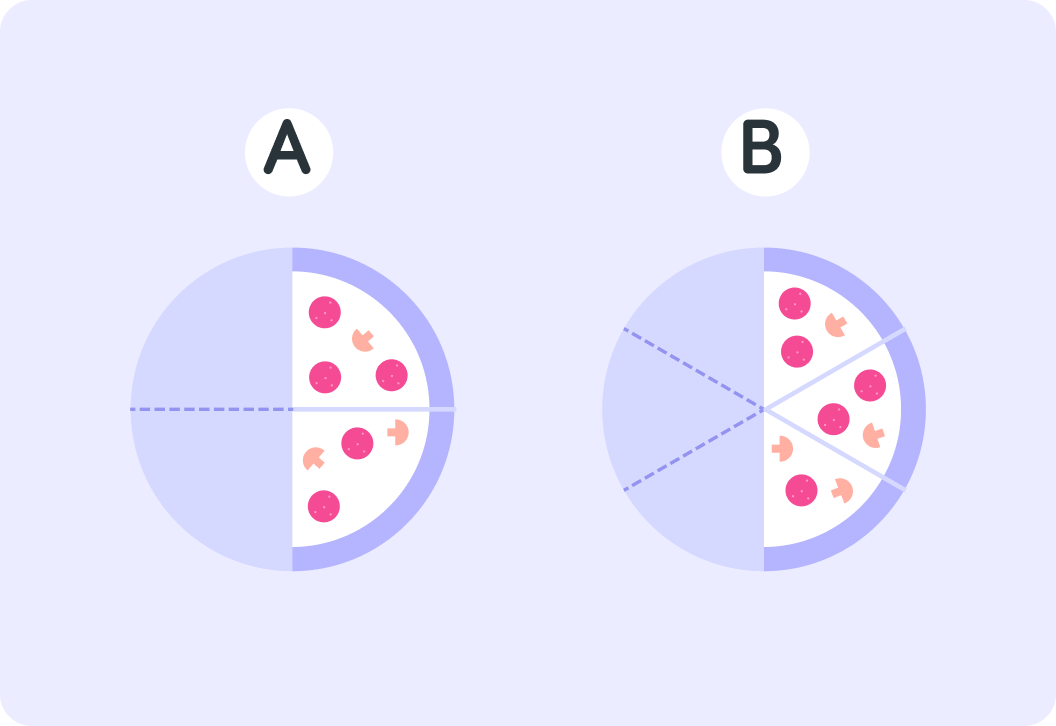
Pizza B was divided into six slices and three are left. What is this as a fraction?

So there are a different number of slices left of each pizza

There are $\dfrac{2}{4}$ slices left of pizza A. There are $\dfrac{3}{6}$ slices left of pizza B.

There are a different number of slices but is this statement true or false?

There is the same amount of pizza left in pizza A and in pizza B.

In both cases, the remaining pizza takes up half a plate

So in fact, $\dfrac{2}{4}$ and $\dfrac{3}{6}$ stand for the same amount. **** We say they are equivalent to "one half" or $\dfrac{1}{2}$ .

You can change for example $\dfrac{3}{6}$ into $\dfrac{1}{2}$ because they are equivalent. To do this, we need to __________ the fraction.

Simplifying fractions

When you simplify a fraction, you make it easier to read. For example, it is much easier to read $\dfrac{1}{2}$ than to read $\dfrac{46}{92}$ .

True or false? There is the same amount of cake left in both cake A and in cake B.

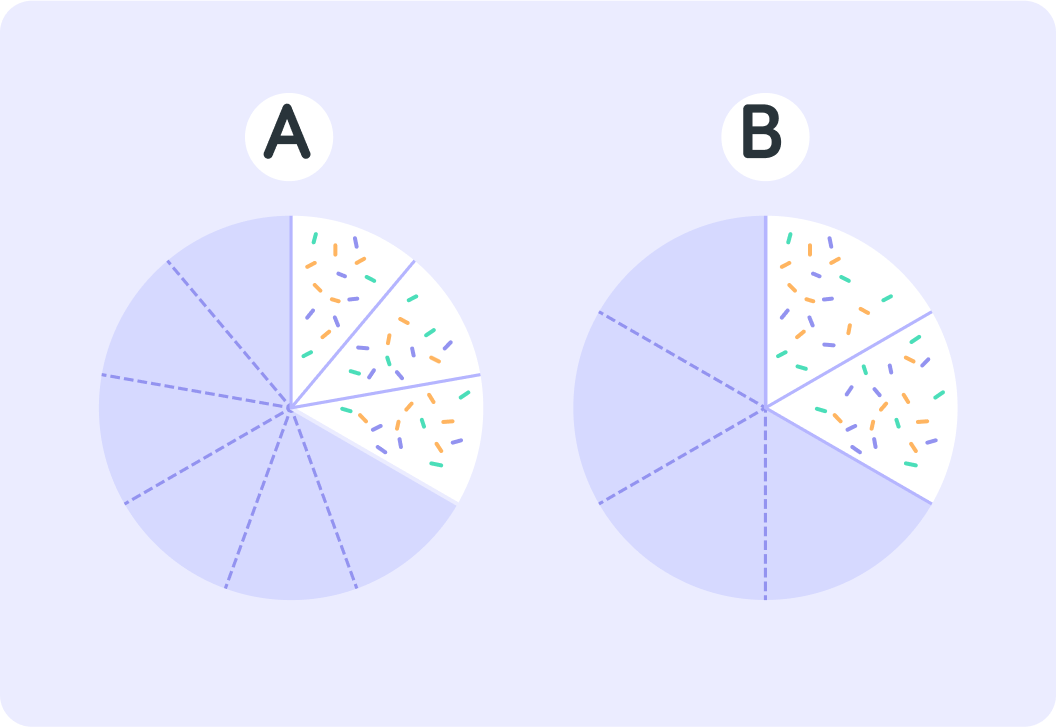
What is the fraction of cake left on plate A?

The fraction of cake on plate B is $\dfrac{2}{6}$ .

This shows that $\dfrac{3}{9}$ and $\dfrac{2}{6}$ are equivalent fractions, they are the same amount of cake.

True or false? You can simplify $\dfrac{3}{9}$ and $\dfrac{2}{6}$ to $\dfrac{1}{3}$ .

Pizza A has four out of eight slices left or $\dfrac{4}{8}$ . What is the simplified equivalent fraction for this?

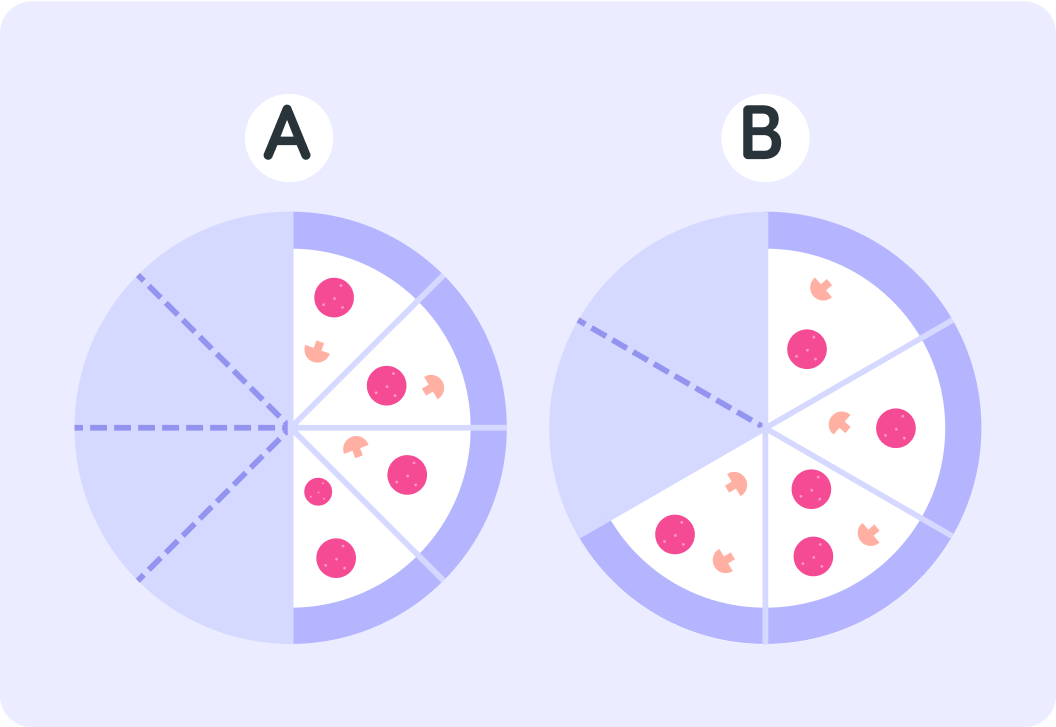
Pizza B has four of six slices left or $\dfrac{4}{6}$ . What is the simplified equivalent fraction to this?

Although both pizzas have four slices left there is more of pizza B left than pizza A.

This shows that $\dfrac{2}{3}$ and $\dfrac{1}{2}$ are not equivalent fractions.

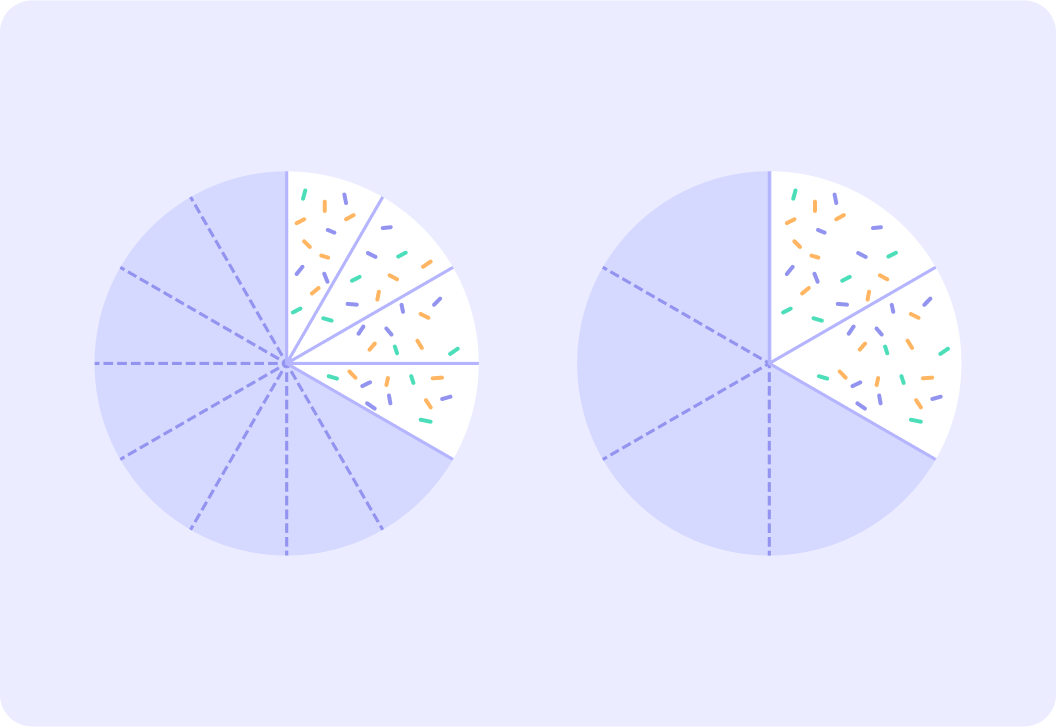
Is it correct to simplify $\dfrac{4}{12}$ to $\dfrac{2}{6}$ ?

However!

If you simplify $\dfrac{4}{12}$ to $\dfrac{2}{6}$ , you haven't simplified the fraction fully - it can be simplified further!

Which fraction is the simplest fraction that is equivalent to $\dfrac{4}{12}$ and $\dfrac{2}{6}$ ?

$\dfrac{1}{3}$ is fully simplified - it is as simplified as it can be

Fractions cannot contain decimals, so you can't change $\dfrac{1}{3}$ into $\dfrac{0.5}{1.5}$ , for example.

How simplifying fractions really works

How do you actually get from $\dfrac{3}{9}$ to $\dfrac{1}{3}$ when simplifying the fraction?

$\dfrac{12}{30}$ can be fully simplified to $\dfrac{2}{5}$ . What number have you divided both the numerator and the denominator by?

When simplifying a fraction you must divide the numerator and the denominator by the same number.

$\dfrac{12\div 6}{30\div 6}=\dfrac{2}{5}$ you can see that the same number is used for both the numerator and the denominator.

You have fully simplified a fraction when there is no number that divides into both the numerator and denominator. Which fraction here is not fully simplified?

Which number can we use to simplify $\dfrac{4}{10}$ ?

We can divide the numerator and denominator in $\dfrac{4}{10}$ by $2$ .

This gives $\dfrac{2}{5}$ which is fully simplified!

Fully simplify $\dfrac{24}{72}$

We can do this in one step or several steps.

First let's notice that both numbers here are even so we can divide them by $2$ . What to we get when we do that $\dfrac{24\div 2}{72\div 2}=$ ?

Is $\dfrac{12}{36}$ fully simplified?

We can simplify further. What happens now $\dfrac{12\div 12}{36\div 12}=$ ?

We have simplified the fraction from $\dfrac{24}{72}$ to $\dfrac{1}{3}$ .

This is now fully simplified!

Fully simplify $\dfrac{12}{15}$ .

Fully simplify $\dfrac{48}{64}$ .

Summary! Simplifying fractions makes them easier to read

The original fraction and the simplified fraction have to represent the same amount.

You have fully simplified a fraction when the numerator and denominator can't get any smaller

This means that there is no number that divides into both the numerator and denominator.

To fully simplify $\dfrac{30}{75}$ : First $\dfrac{30\div 5}{75\div 5}=\dfrac{6}{15}$ and then $\dfrac{6\div 3}{15\div 3}=\dfrac{2}{5}$ .

Or do it in one step $\dfrac{30\div 15}{75\div 15}=\dfrac{2}{5}$