Number

YOU ARE LEARNING:

Top-Heavy Fractions and Mixed Numbers

When the fraction is top-heavy (when the numerator is larger than the denominator), you can express it as a mixed number.

Here we have three halves of cake. How would you write this as a fraction?

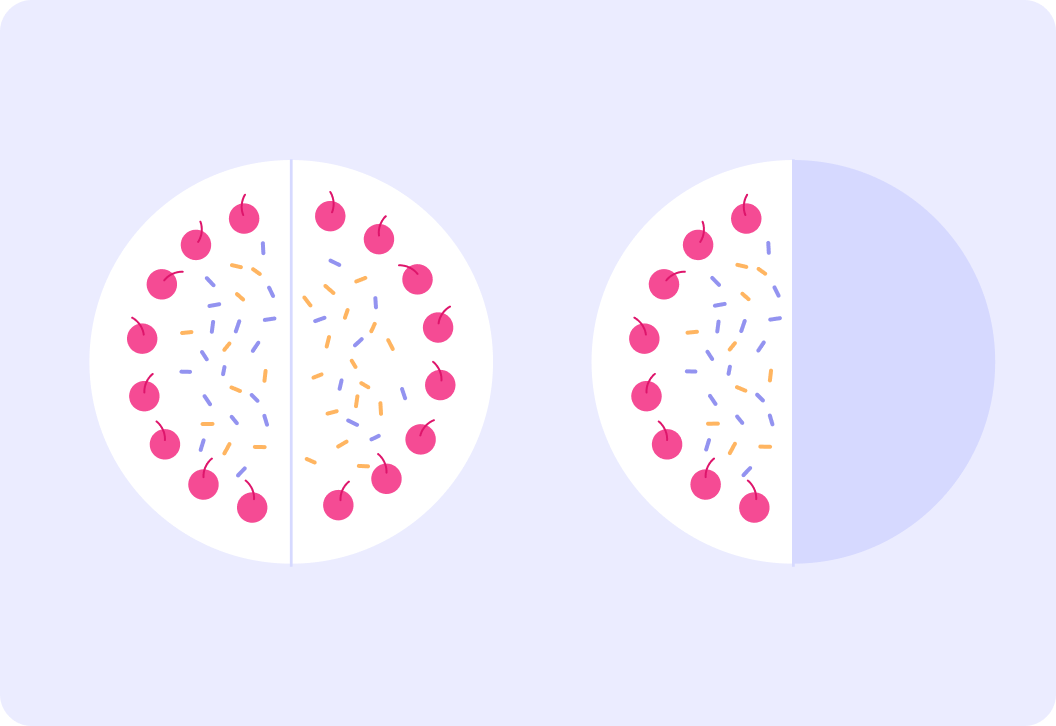
Here we have three halves or $\dfrac{3}{2}$ of cake.

This is a top heavy fraction.

We can see that $\dfrac{3}{2}$ of cake is more than one whole cake. What is an alternative way of writing $\dfrac{3}{2}$ ?

What do you think we call numbers like $1\dfrac{1}{2}$ ?

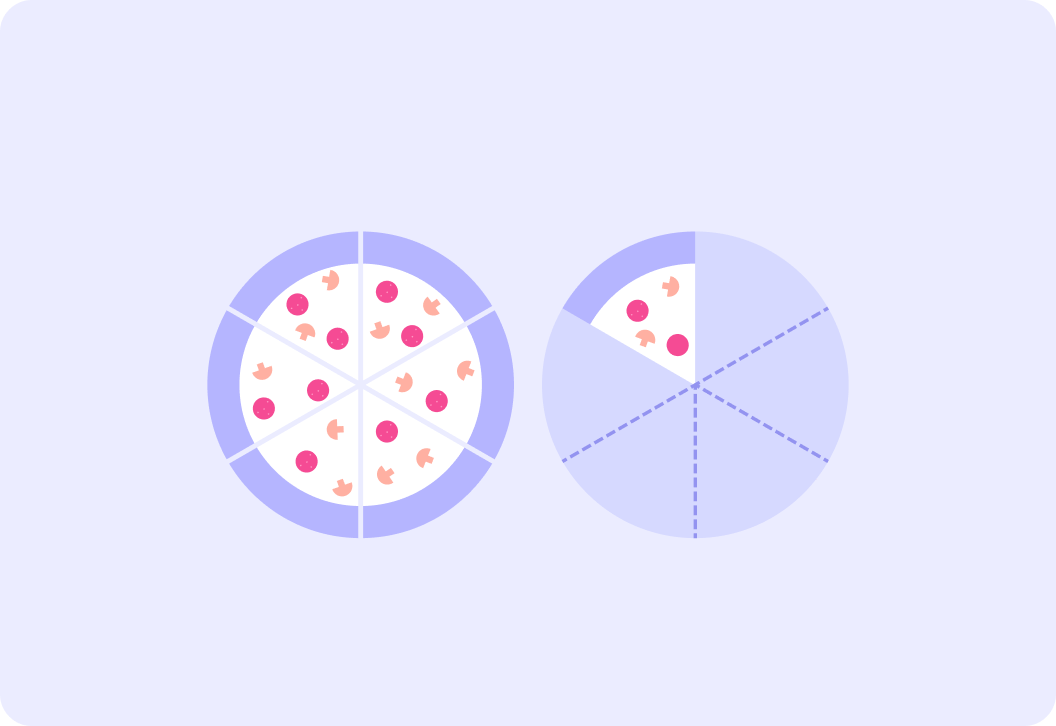
Each of these pizzas was divided into five slices. How many slices are left?

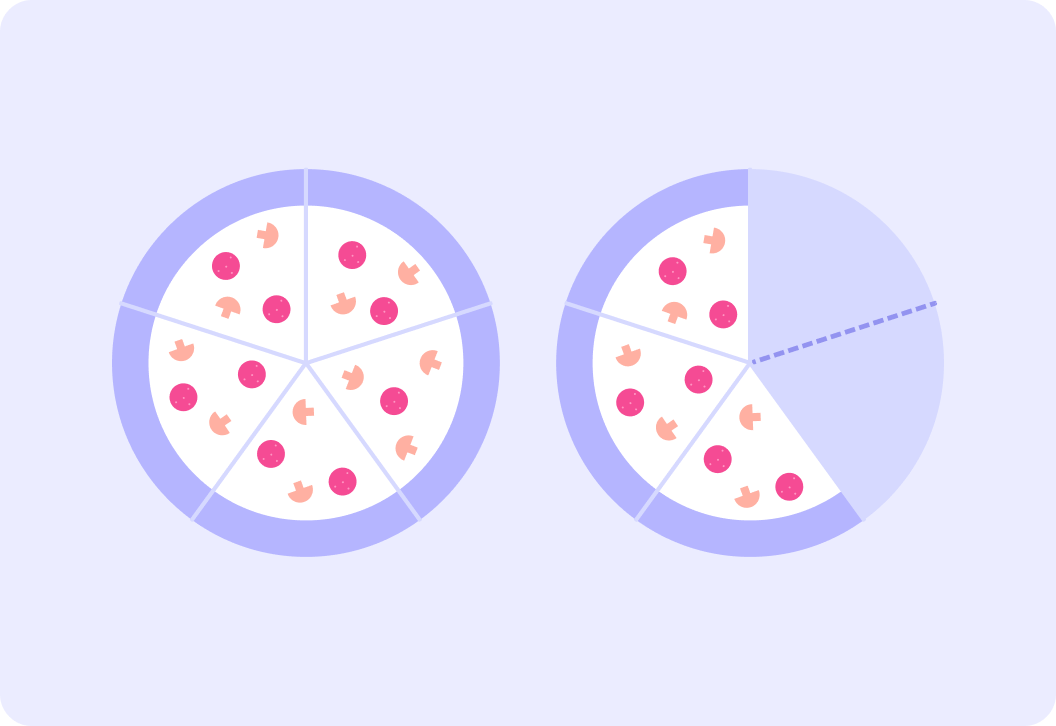
We know we have more than one pizza so we can expect a top heavy fraction. How do we write the eight slices as a top heavy fraction?

We have $\dfrac{8}{5}$ of pizza, but how would you write it as a mixed number?

So there are $\dfrac{8}{5}$ pizzas here which we can also write as $1\dfrac{3}{5}$ .

But how did we get from $\dfrac{8}{5}$ to $1\dfrac{3}{5}$ ?

The whole pizza is divided into five slices and all five are still on the plate. How do we write this part as a fraction?

So we've taken $\dfrac{5}{5}$ and replaced it with $1$ .

We started with $\dfrac{8}{5}$ , after taking five away there are three left and that's how we get $1\dfrac{3}{5}$ .

Try this one. The amount of cake as a top heavy fraction is $\dfrac{5}{3}$ . How would you write it as a mixed number?

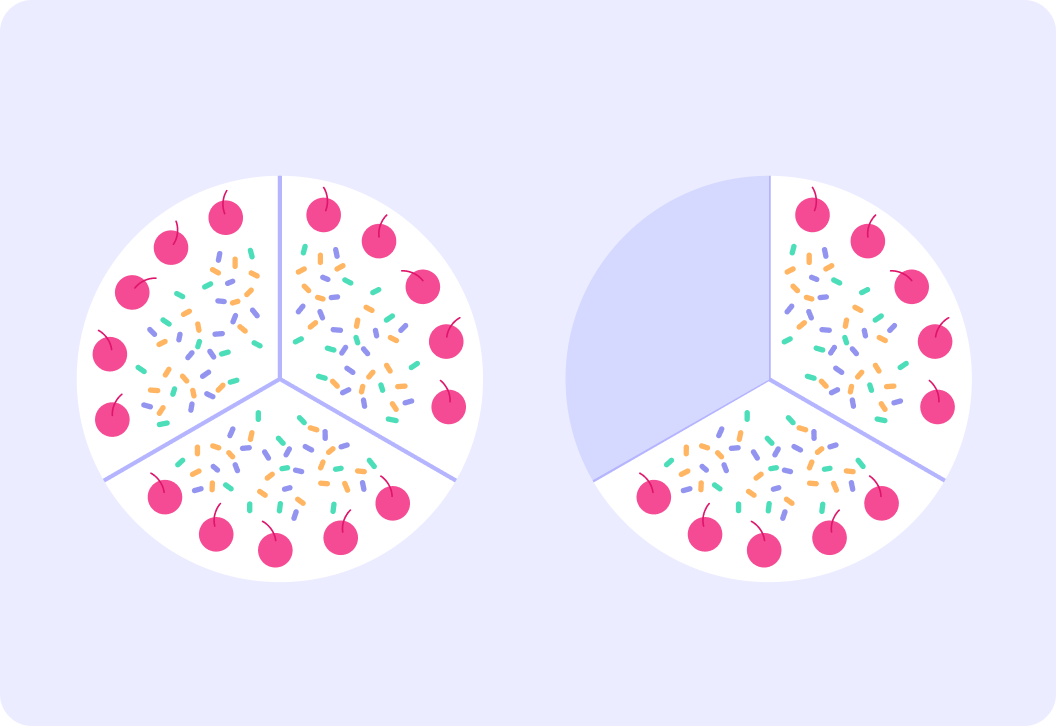
How would you write $\dfrac{7}{4}$ as a mixed number?

Try another one: what is $\dfrac{9}{2}$ as a mixed number?

We have converted top heavy fractions to mixed numbers.

This time we will go the other way and convert a mixed number into a top heavy fraction.

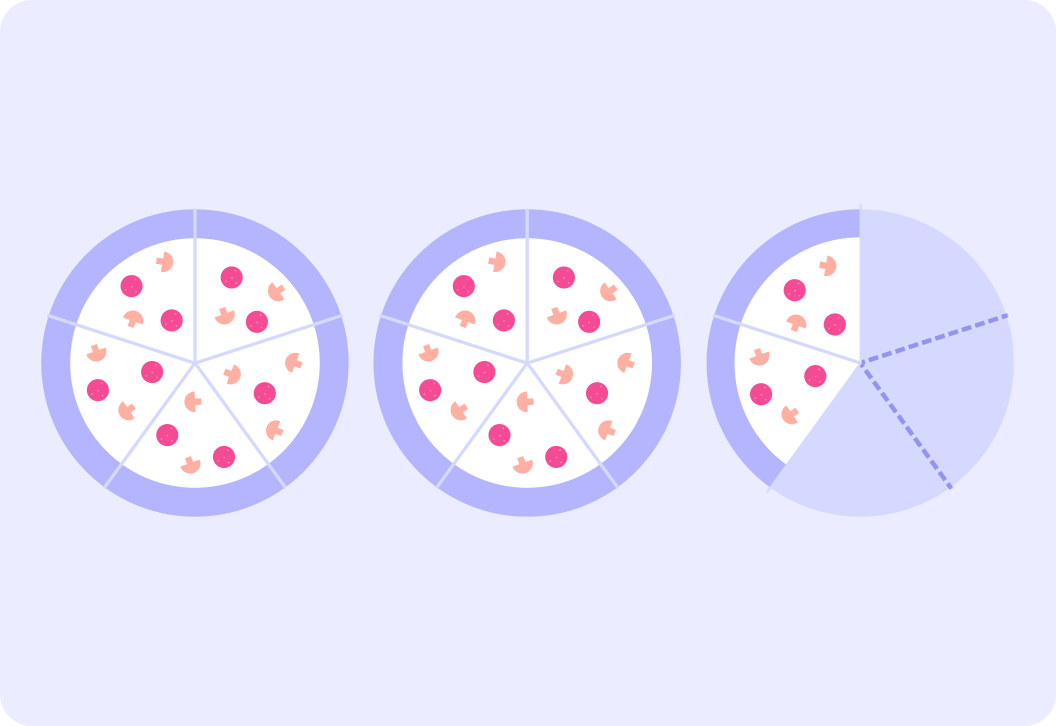
Looking at the image we can see we have two whole pizzas and a fraction of a pizza. What is this as a mixed number?

Our mixed number is $2\frac{2}{5}$ .To convert into a top heavy fraction, we need to know how many slices there are in the two whole pizzas. Write this as a top heavy fraction.

We have seen that we can replace our two whole pizzas or the $2$ with $\frac{10}{5}$

We add the $\dfrac{10}{5}$ to the $\dfrac{2}{5}$ to give a total of $\dfrac{12}{5}$ .

We started with a mixed number $2\dfrac{2}{5}$ and found out how many slices are in the two whole pizzas.

This gave us the answer that $2\dfrac{2}{5}=\dfrac{12}{5}$ .

How do you write the mixed number $3\dfrac{2}{3}$ as a top heavy fraction?

Summary! Fractions can be top heavy

That means the numerator is bigger than the denominator, for example $\dfrac{7}{6}$

Top heavy fractions and mixed numbers are greater than $1$

For example, $\dfrac{6}{6}$ is the same as $1$ , so $\dfrac{7}{6}$ has a whole and an "extra" sixth.

You can turn top heavy fractions into mixed numbers

For example, $\dfrac{7}{6}$ is the same as the mixed number $1\dfrac{1}{6}$ .

We can turn mixed numbers into top heavy fractions.

For example, $2\dfrac{2}{5}$ is the same as the top heavy fraction $\dfrac{12}{5}$ .