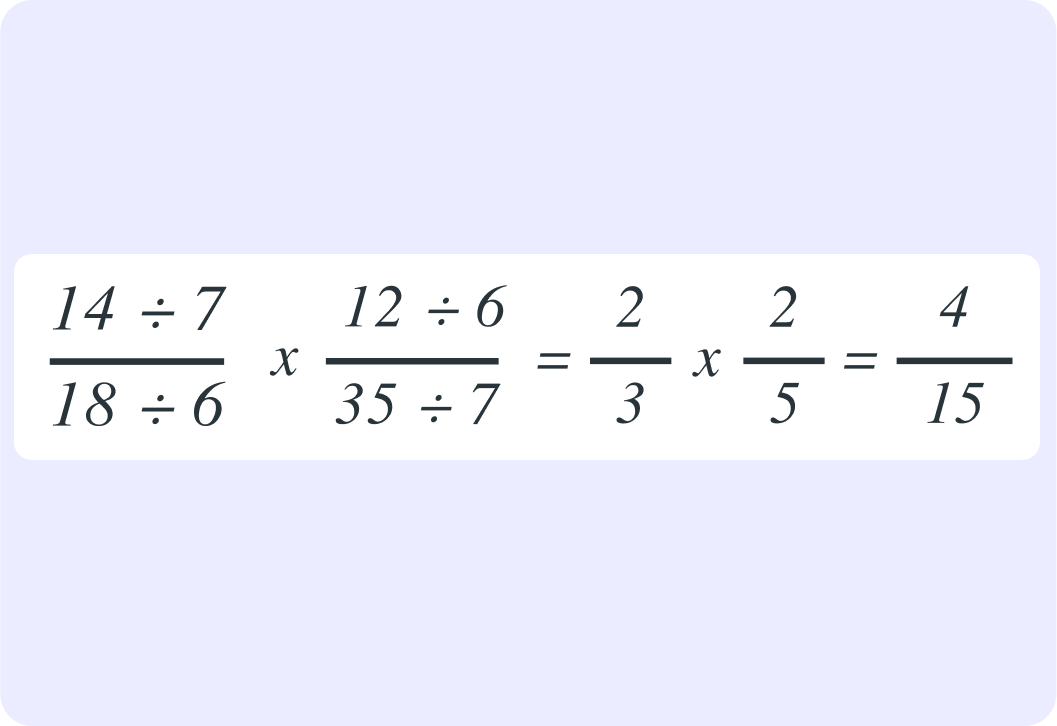Number

YOU ARE LEARNING:

Multiplying Fractions

Multiplying Fractions

You can multiply fractions following a particular rule.

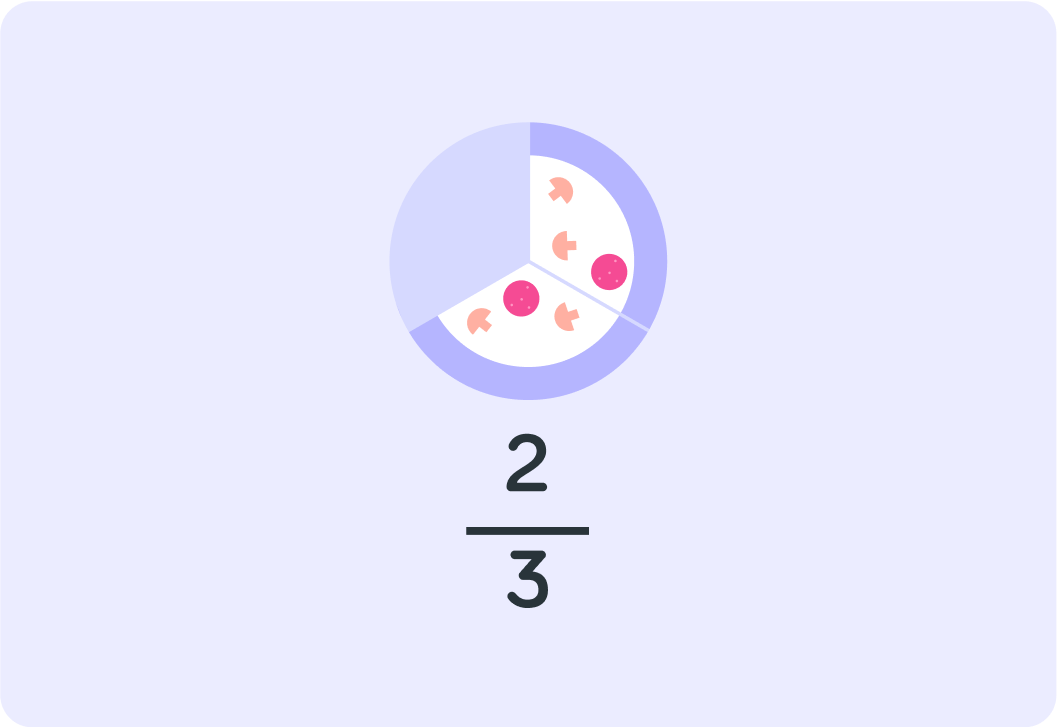
How much of this pizza is left? Give your answer as a fraction.

If you wanted to split the left-over pizza evenly between two people they would each get _______ of the remaining pizza.

A) half B) a third C) all

So two people split the left-over pizza so they each get half of the remaining pizza

You can express that with fractions like this $\frac{2}{3}\times \frac{1}{2}$

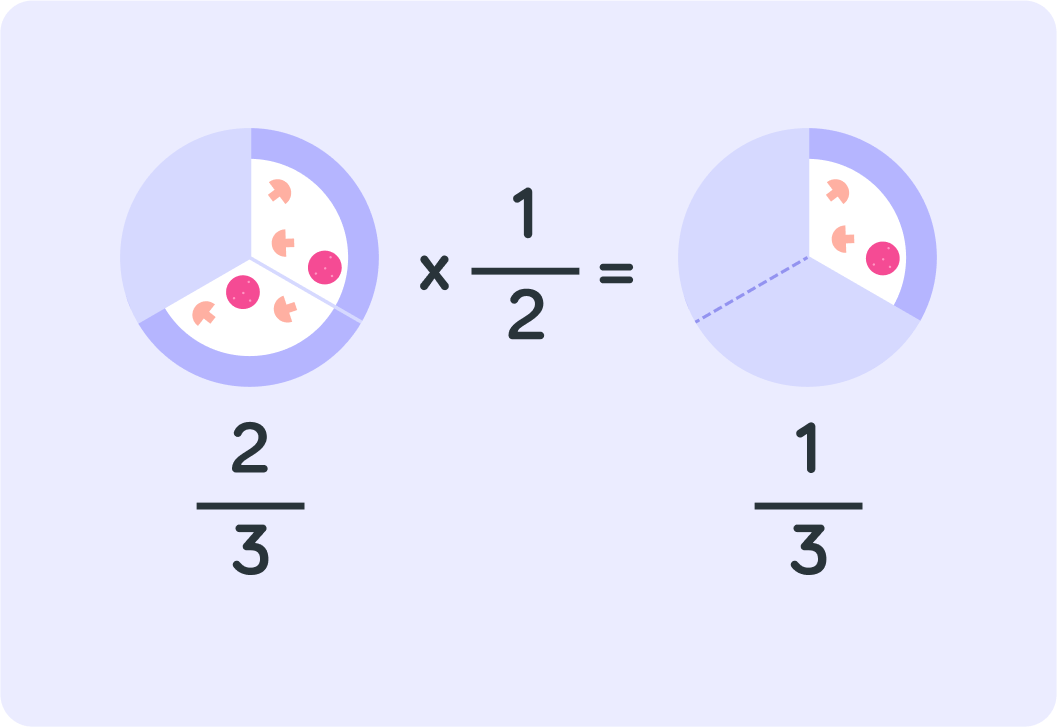
How much of the original whole pizza does each of the two people get? Give your answer as a fraction.

Each of the two people will get $\frac{1}{3}$ of the original pizza

So $\frac{2}{3} \times \frac{1}{2}=\frac{1}{3}$

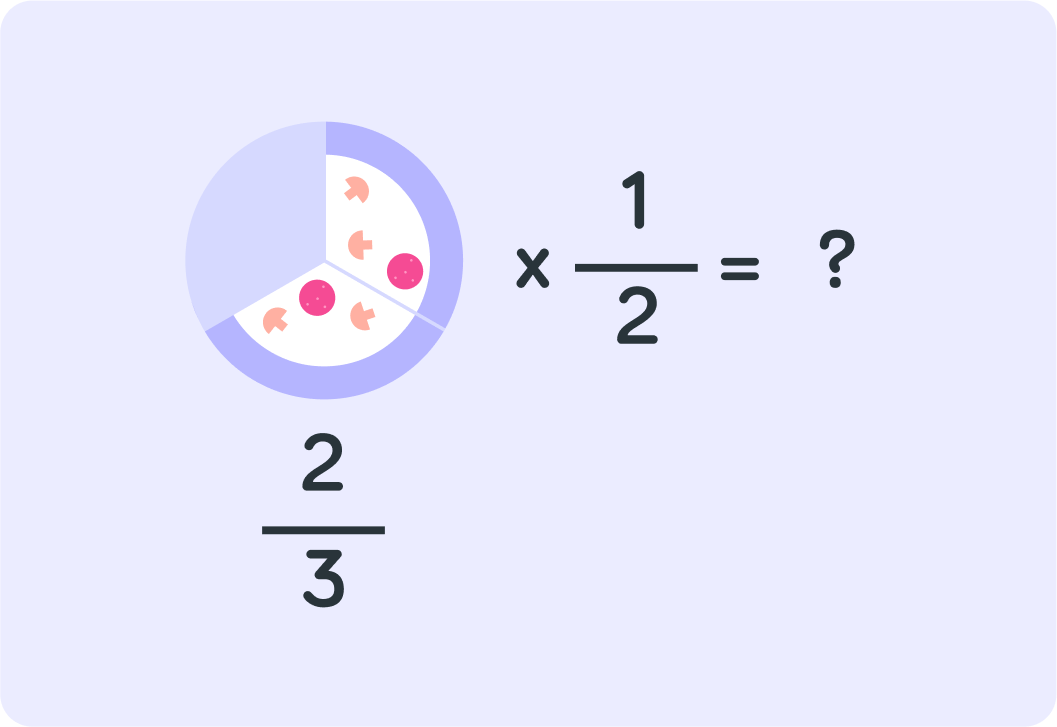
What if you didn't want to split the remaining $\frac{2}{3}$ between 2 people?

What if you wanted to split it between 3 people?

When you split between 2 people, you multiplied by $\frac{1}{2}$ . If you split between 3 people, you multiply by...

In order to split the left-over pizza evenly, you can split up each of the slices into thirds

This is the same as if the pizza had originally been divided into 9 slices.

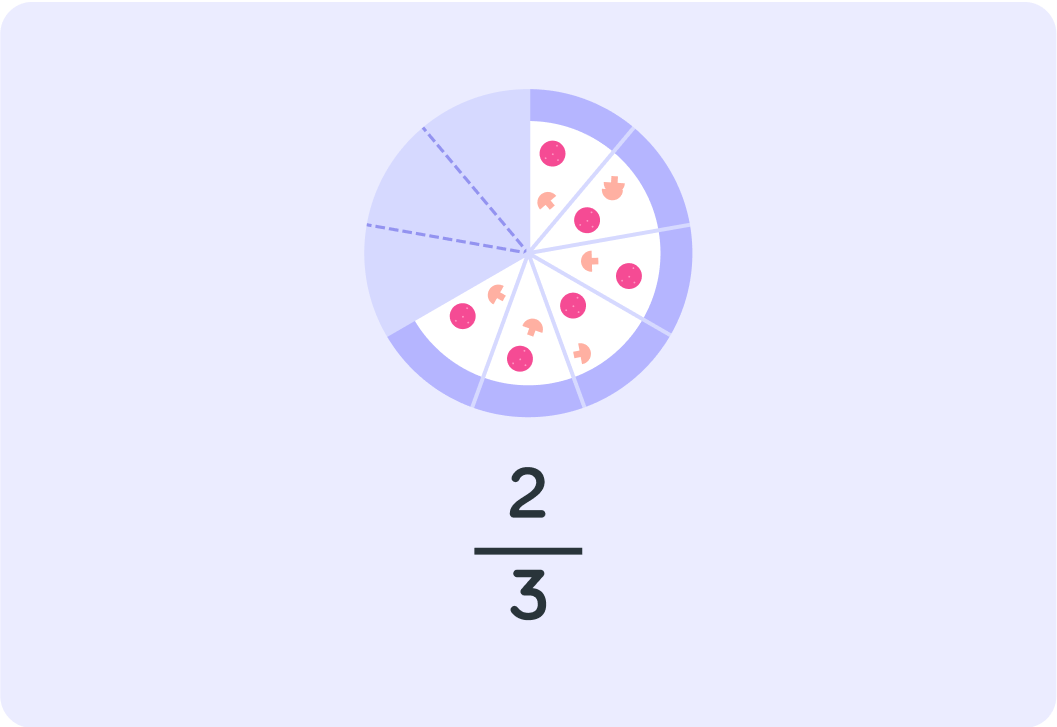
How many slices are left of this pizza now after it has been divided into 9ths?

There are 6 remaining slices and 3 people - if each person gets the same number of slices, how many slices does each person get?

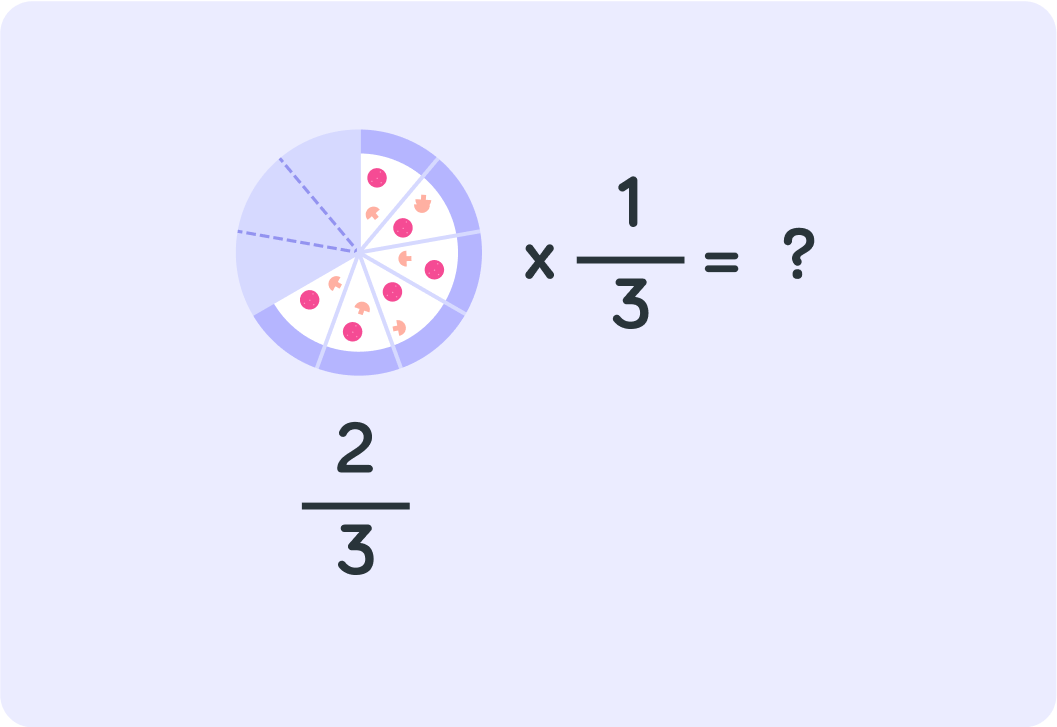
So each of the 3 people get 2 out of the 9 slices in the original pizza. How do you write that as a fraction?

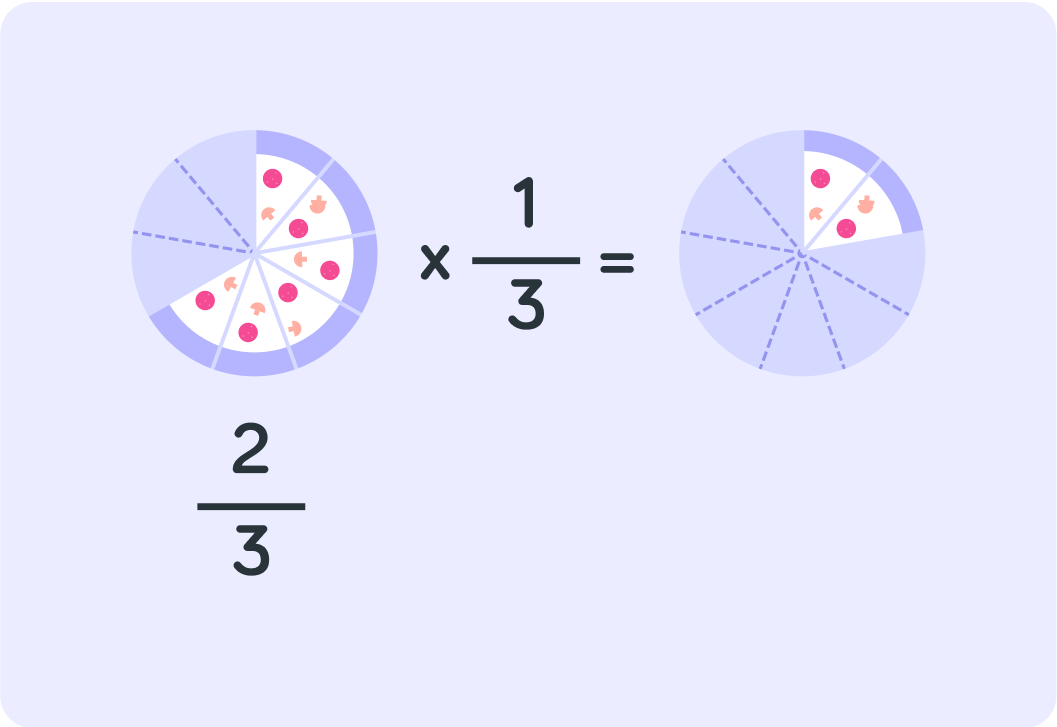
So!

$\frac{2}{3} \times \frac{1}{3}=\frac{2}{9}$

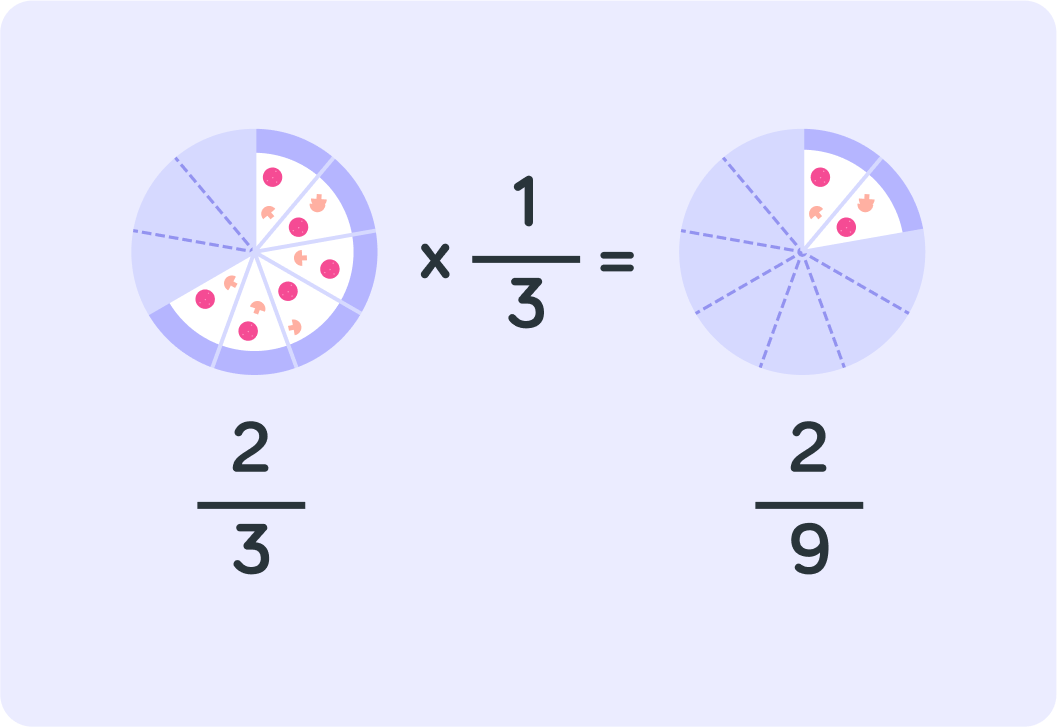
Now, look only at the maths in this example

How did you actually get from $\frac{2}{3} \times \frac{1}{3}$ to $\frac{2}{9}$ ?

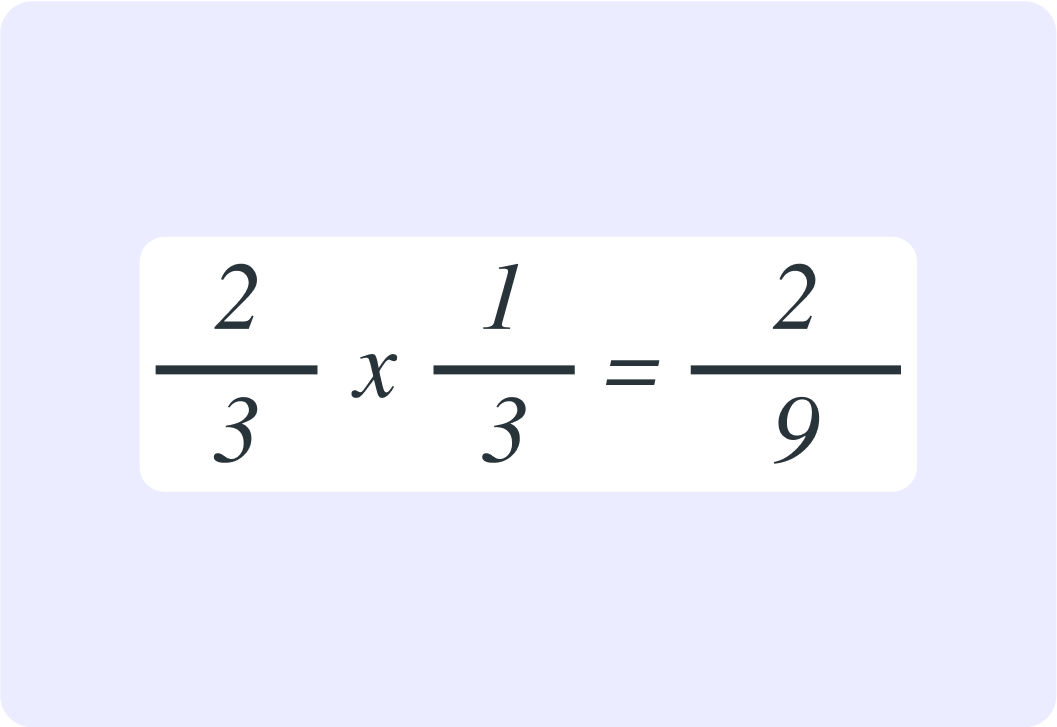
You got to the denominator $9$ by ______________ the denominators in the other fractions.

A) adding B) multiplying

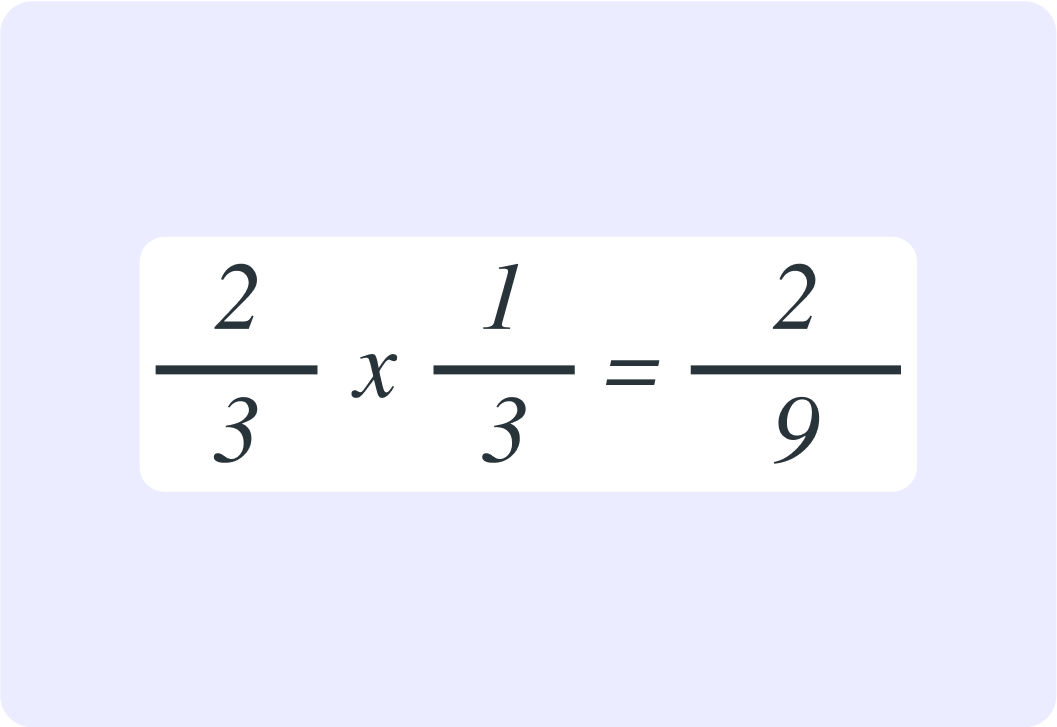
You also got to the numerator $2$ in the result by ______________ the numerators in the other fractions.

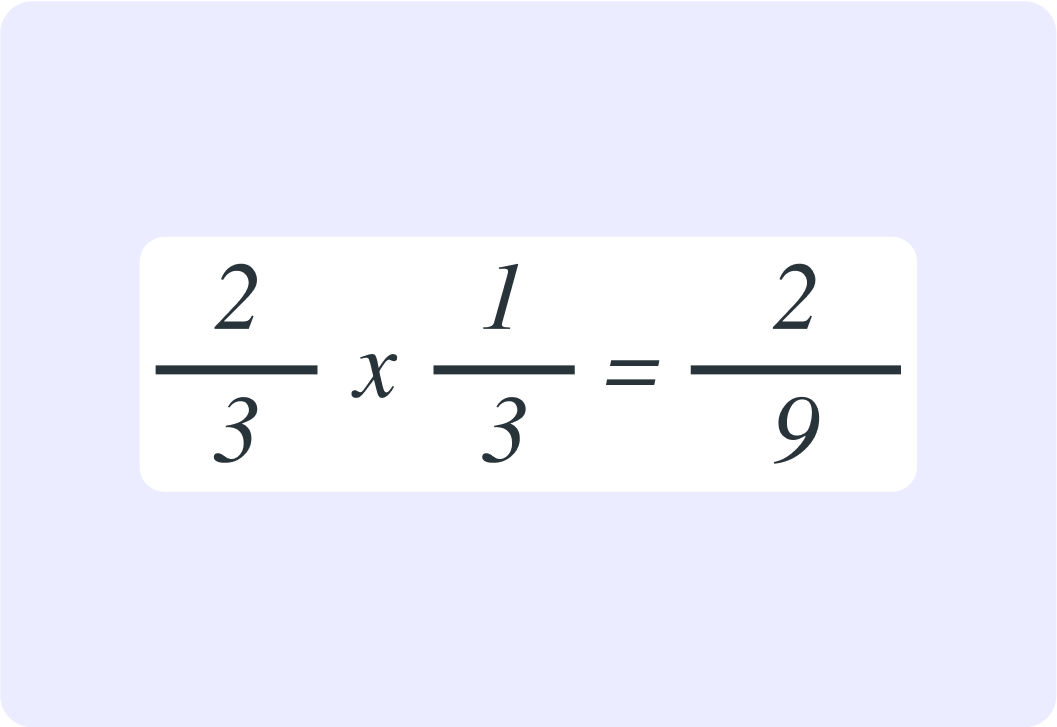
So you multiply two fractions by multiplying the numerators and the denominators. How do you write that in a generalised form?

A) $\frac{a}{c} \times \frac{b}{d}=\frac{a + b}{c + d}$ B) $\frac{a}{c} \times \frac{b}{d}=\frac{a \times b}{c \times d}$

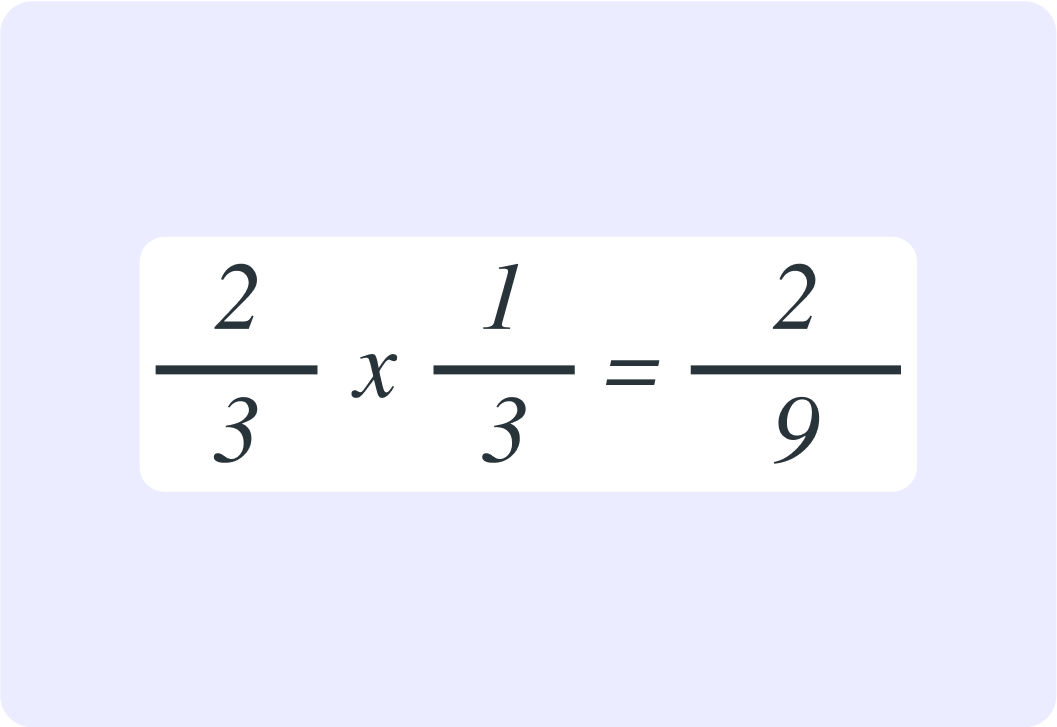
So you multiply two fractions like this

$\frac{a}{c} \times \frac{b}{d}=\frac{a \times b}{c \times d}$

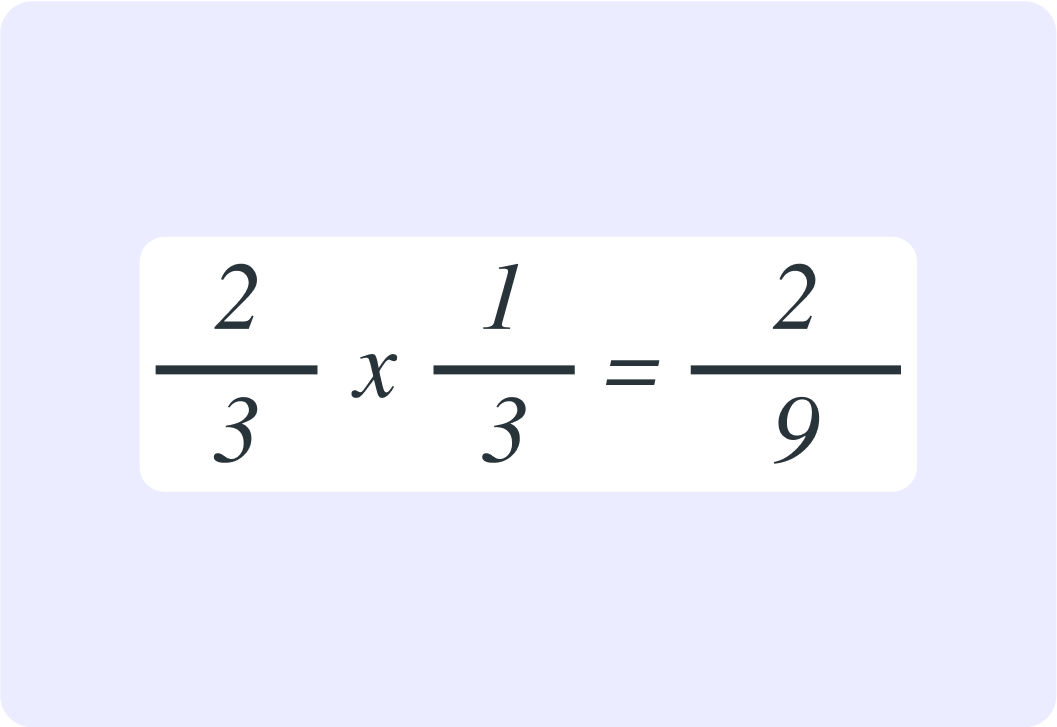
What is $\frac{4}{5} \times \frac{2}{3}$ ? Give your answer as a fraction.

What is $\frac{3}{6}\times\frac{4}{3}$ ? Give your answer as a fully simplified fraction.

Sometimes you end up having to multiply numbers that aren't super easy to multiply

For example, here you are meant to multiply $21$ and $25$

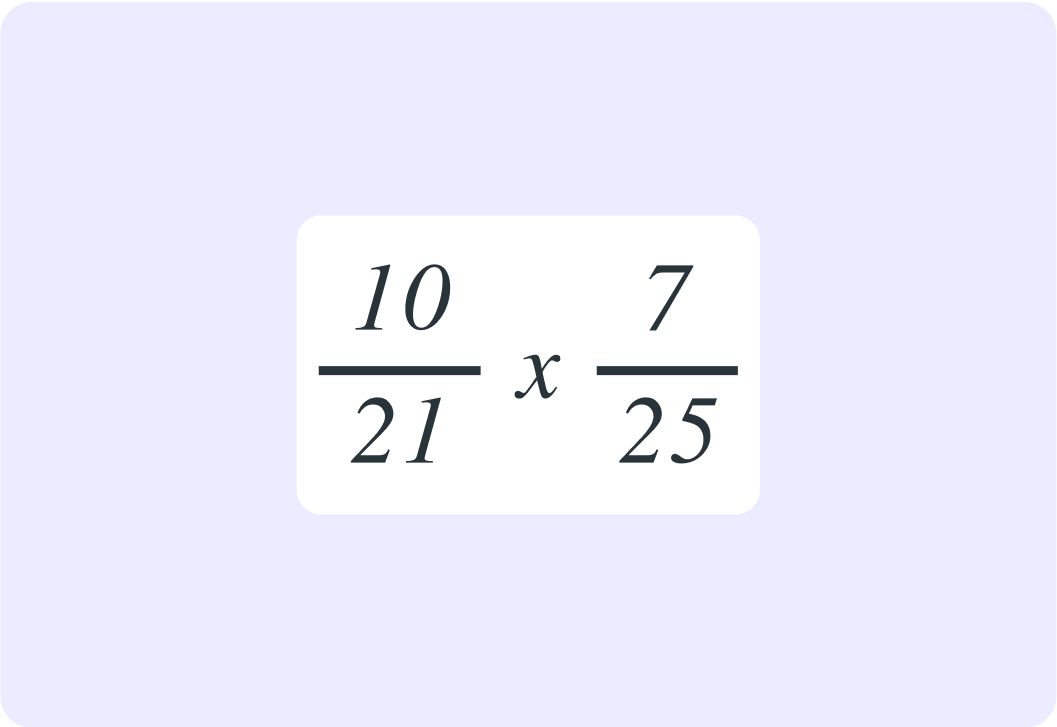
There is a trick!

If you can find a number that both the numerator of one fraction and the denominator of the other fraction can be divided by, you can make the problem easier.

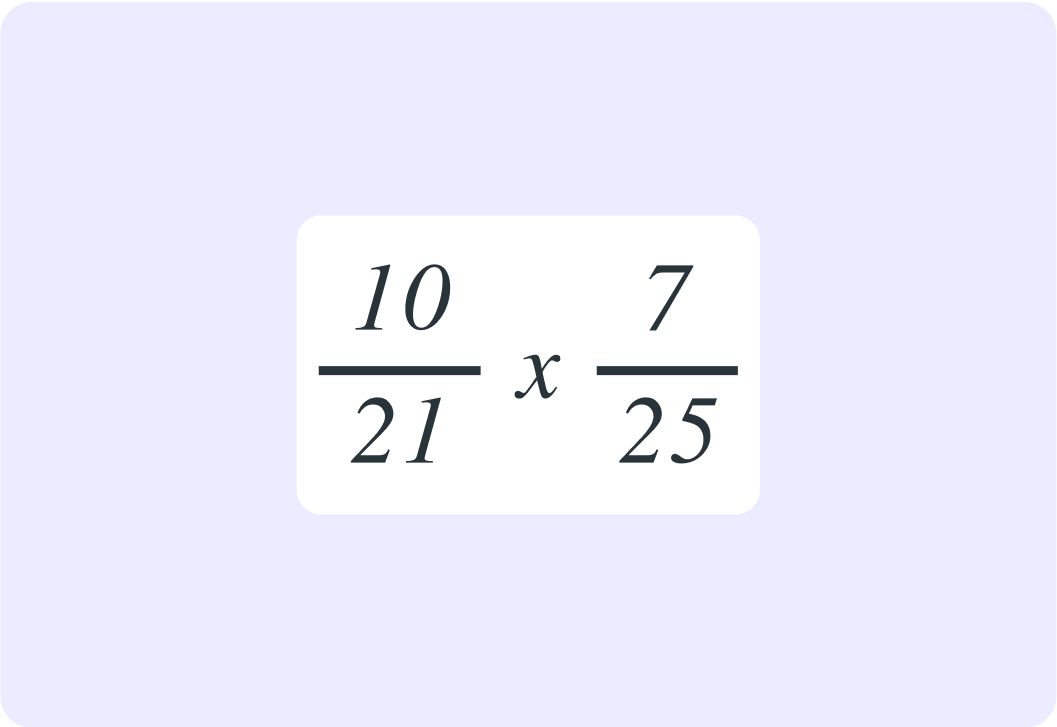
What is the highest number that both $10$ and $25$ can be divided by (their highest common factor)?

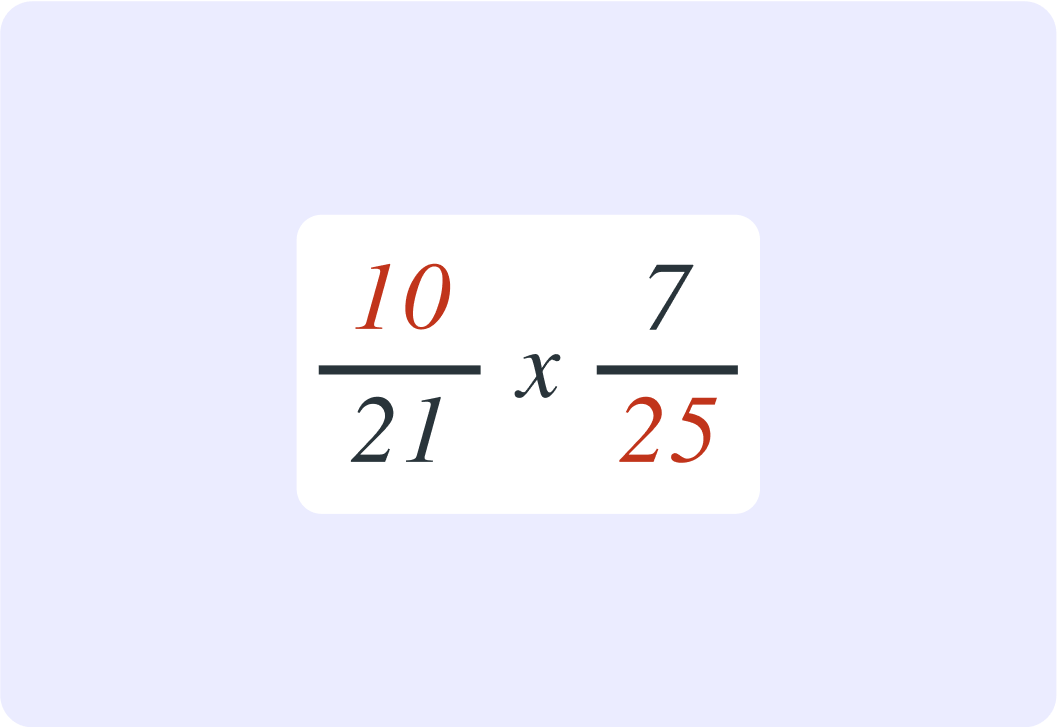
So you can now simplify by dividing that numerator and that denominator by $5$

$\frac{10 \div 5}{21} \times \frac{7}{25 \div 5} = \frac{2}{21} \times \frac{7}{5}$

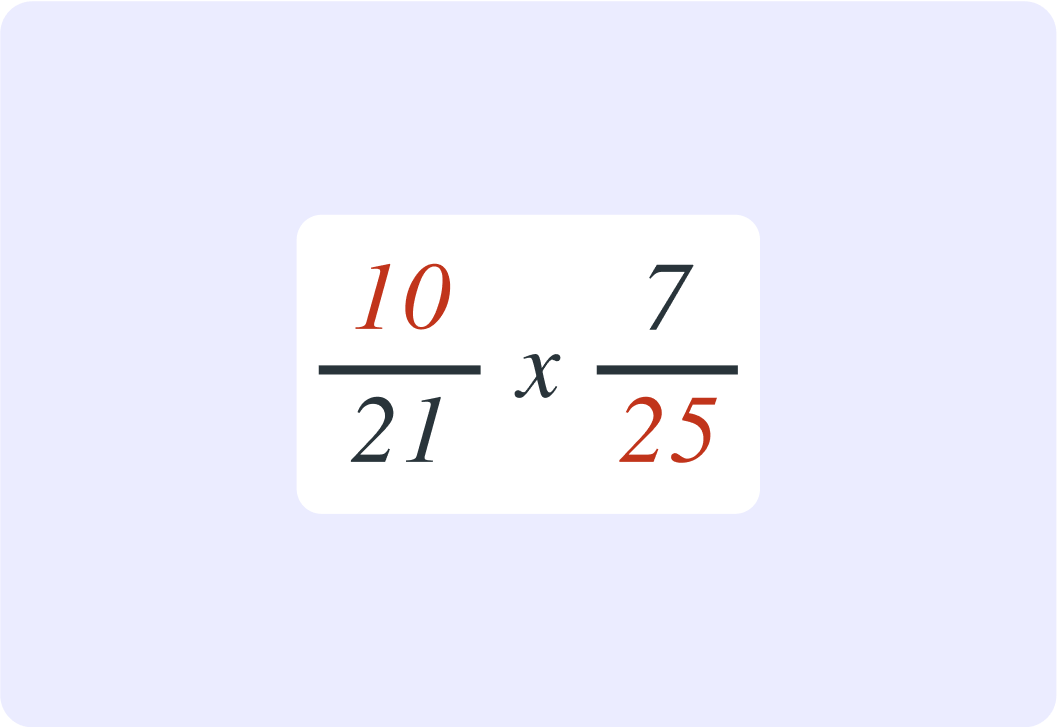
What is the highest common factor between $7$ and $21$ ?

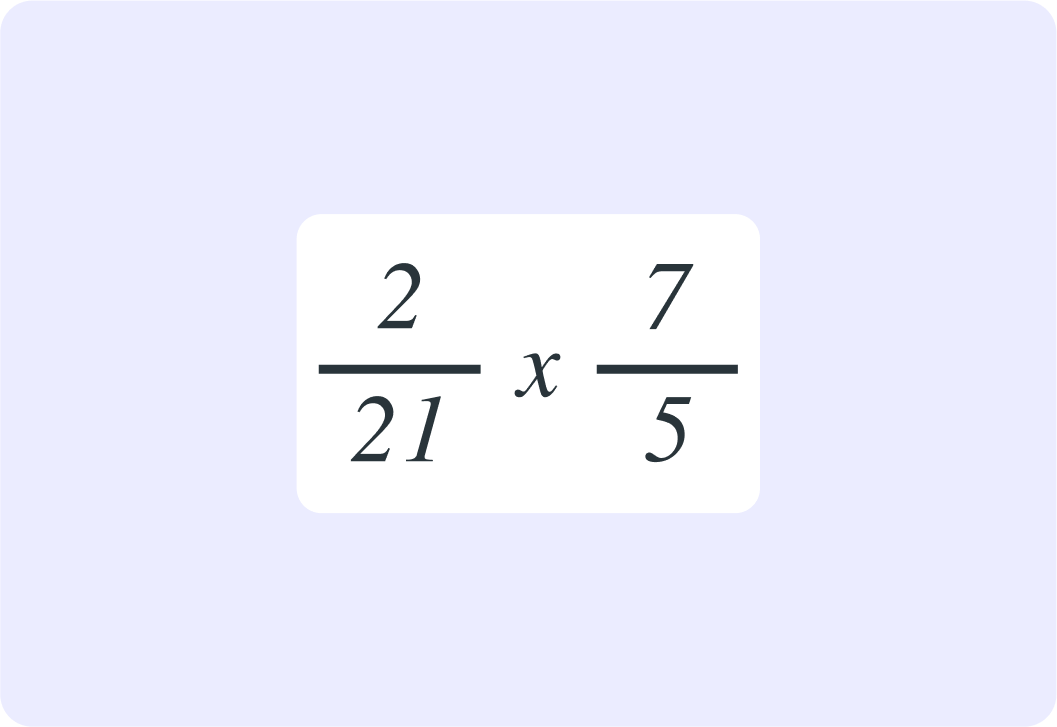
So you can now simplify further by dividing that numerator and that denominator by $7$

$\frac{2}{21 \div 7} \times \frac{7 \div 7}{5} = \frac{2}{3} \times \frac{1}{5}$

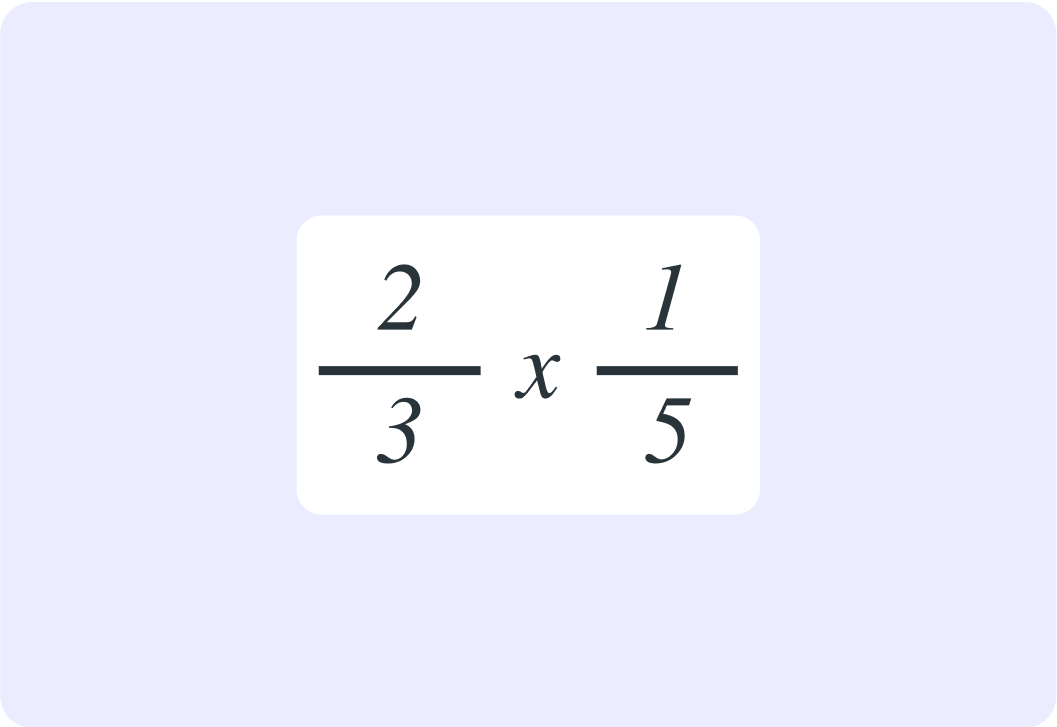
So now you have simplified $\frac{10}{21} \times \frac{7}{25}$ to $\frac{2}{3} \times \frac{1}{5}$ . What is the result as a fraction?

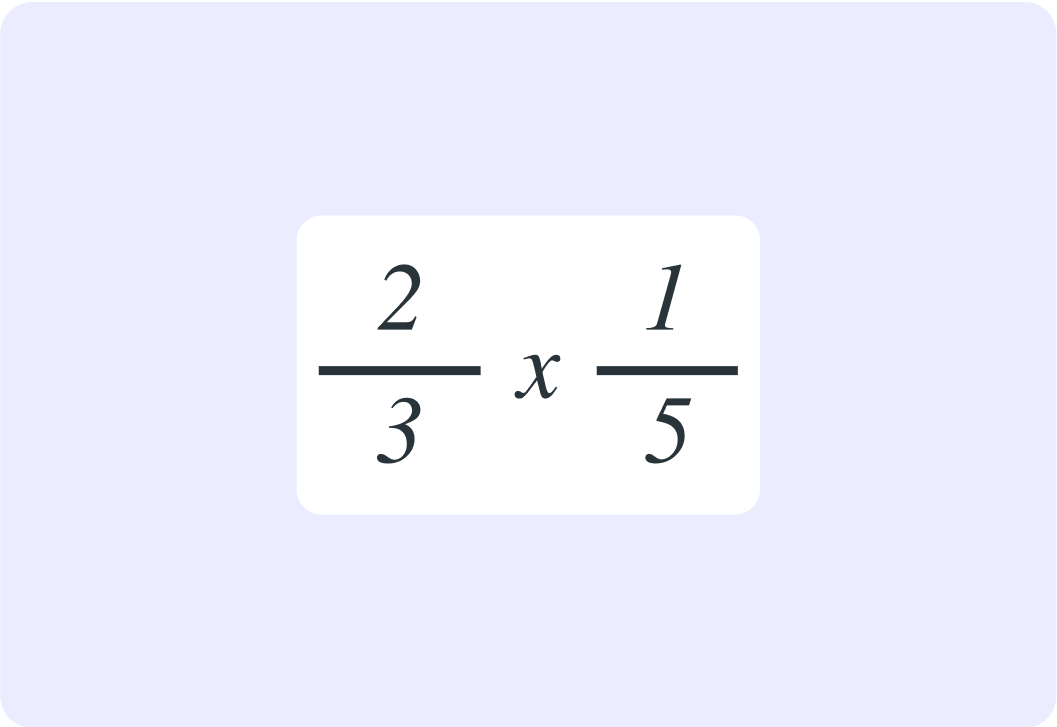
It would also be good to simplify this problem

You need to find the highest common factor between the numerator of one fraction and the denominator of the other fraction.

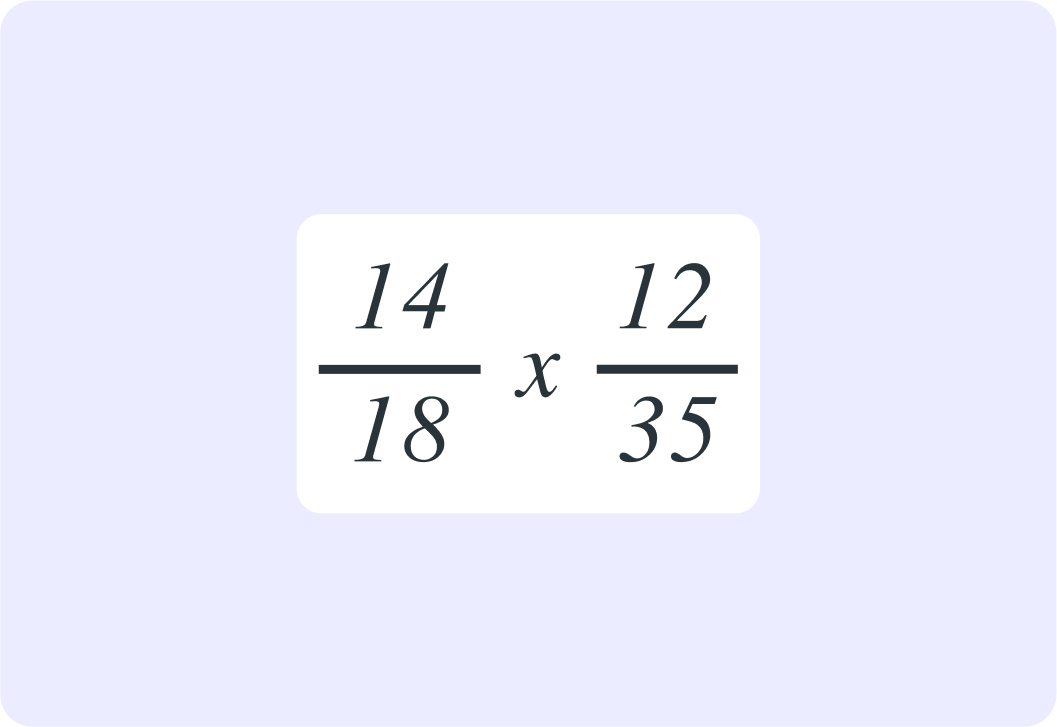
What is the highest common factor between $14$ and $35$ ?

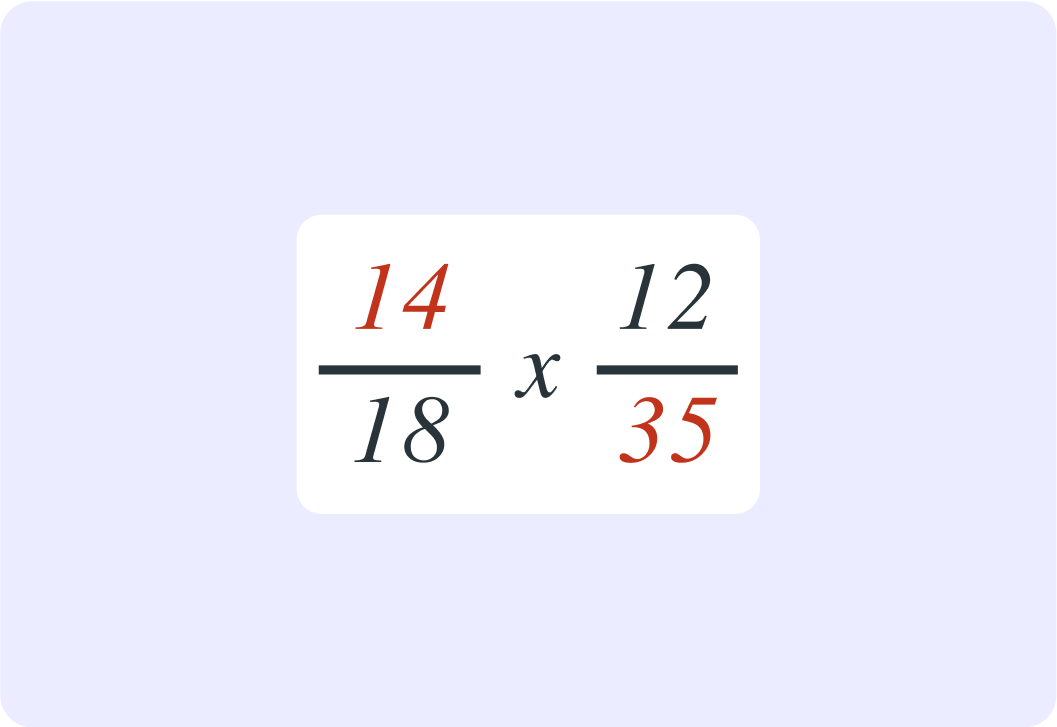
What is the highest common factor between $18$ and $12$ ?

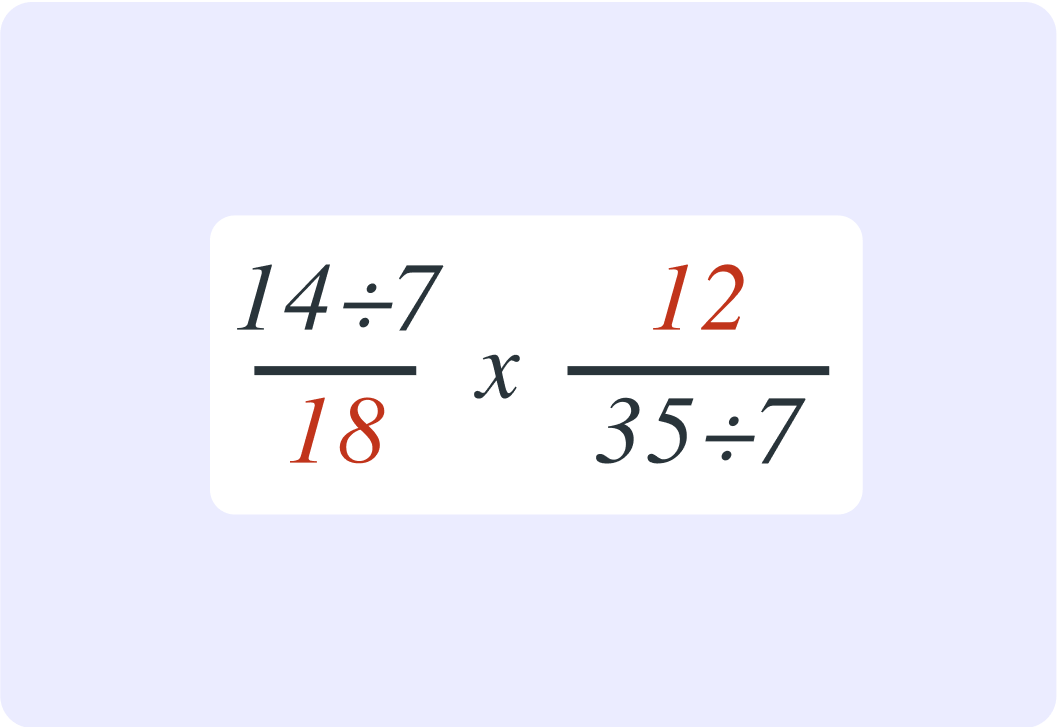
So now you have simplified $\frac{14}{18} \times \frac{12}{35}$ to $\frac{2}{3} \times \frac{2}{5}$ . What is the result as a fraction?

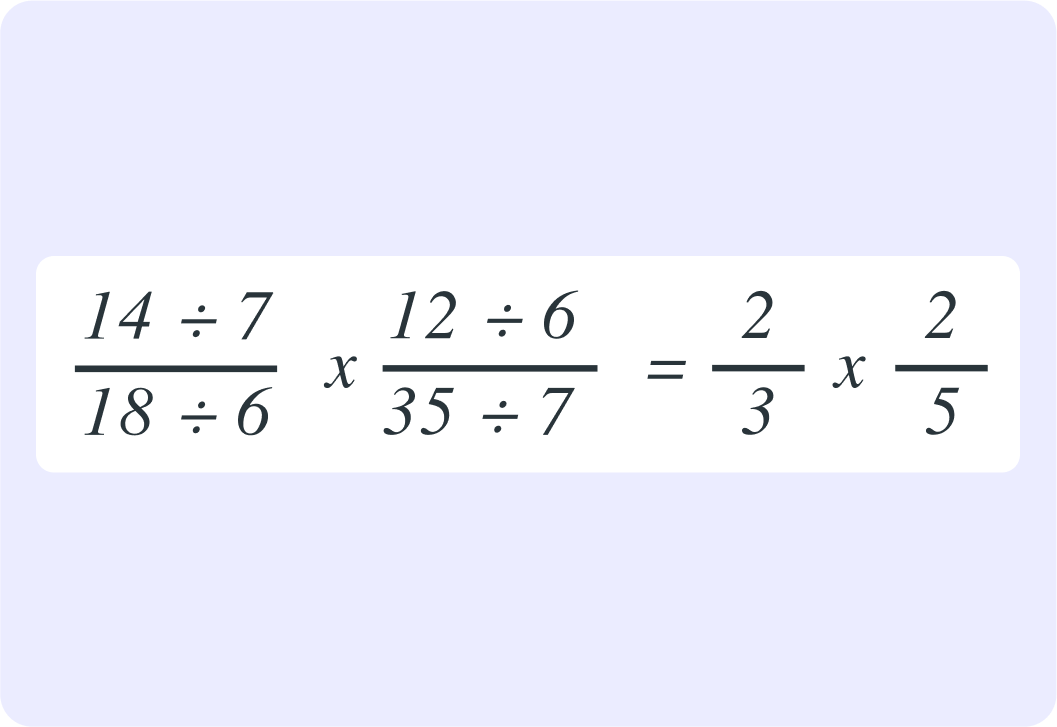
So you could simplify $\frac{14}{18} \times \frac{12}{35}$ to $\frac{2}{3} \times \frac{2}{5}$

That made it easier to work out that $\frac{14}{18} \times \frac{12}{35} = \frac{4}{15}$

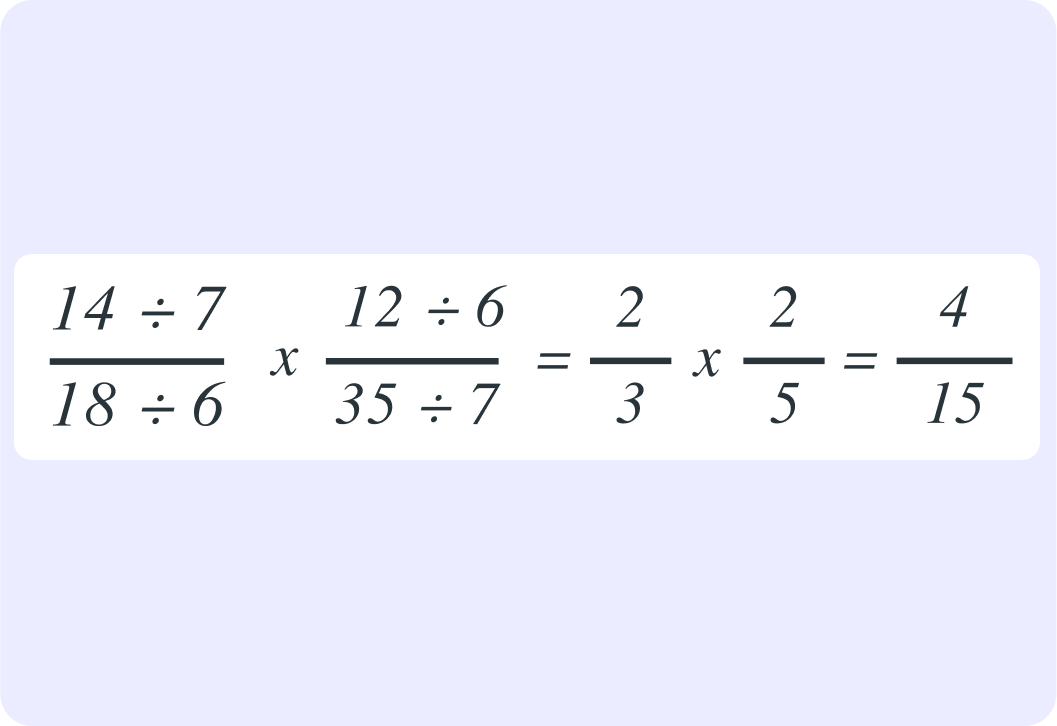
Simplify $\frac{16}{24} \times \frac{4}{32}$ and give your answer as a fully simplified fraction.

Summary! You can multiply a fraction with another fraction

You multiply the numerators in the two fractions and then the denominators.

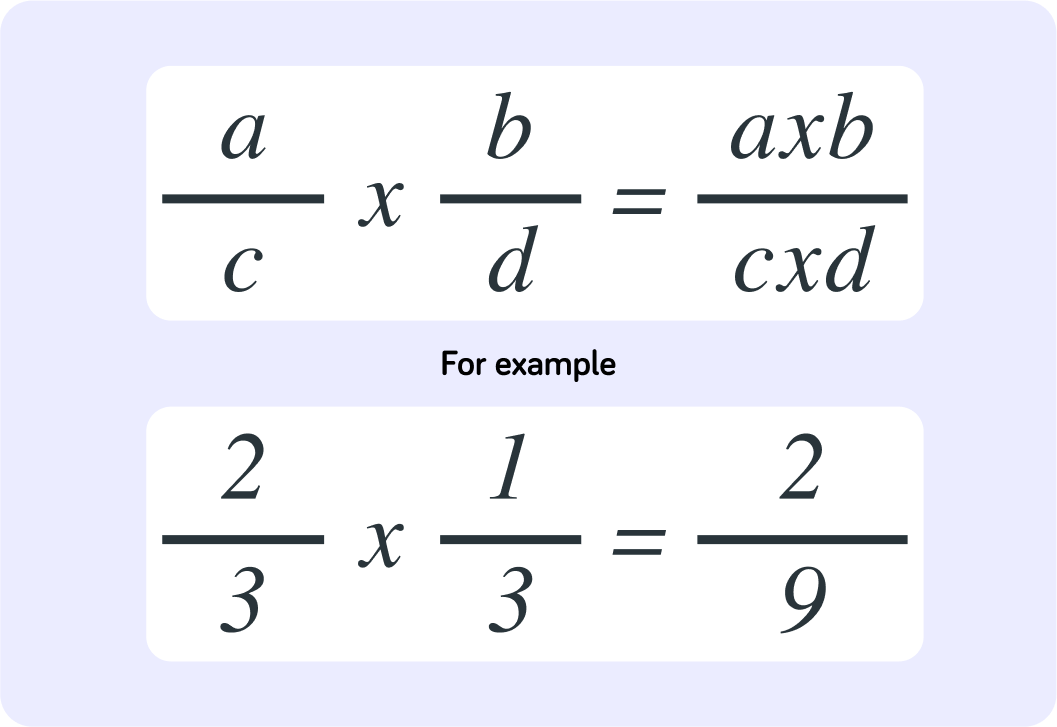
If the multiplication is complicated, you can try to simplify the problem

You find the highest common factor between the numerator in one fraction and the denominator in the other fraction.