Probability & Statistics

YOU ARE LEARNING:

Probability and Algebraic Problems

Probability and Algebraic Problems

We can use probability tree diagrams to solve algebraic problems, and find probabilities of events happening.

Some probability problems involve algebra, and we can represent these problems using probability tree diagrams.

2 balls are picked at random from a bag

There are $n$ total green and yellow balls. 3 of the balls are green. The ball is replaced after the first pick.

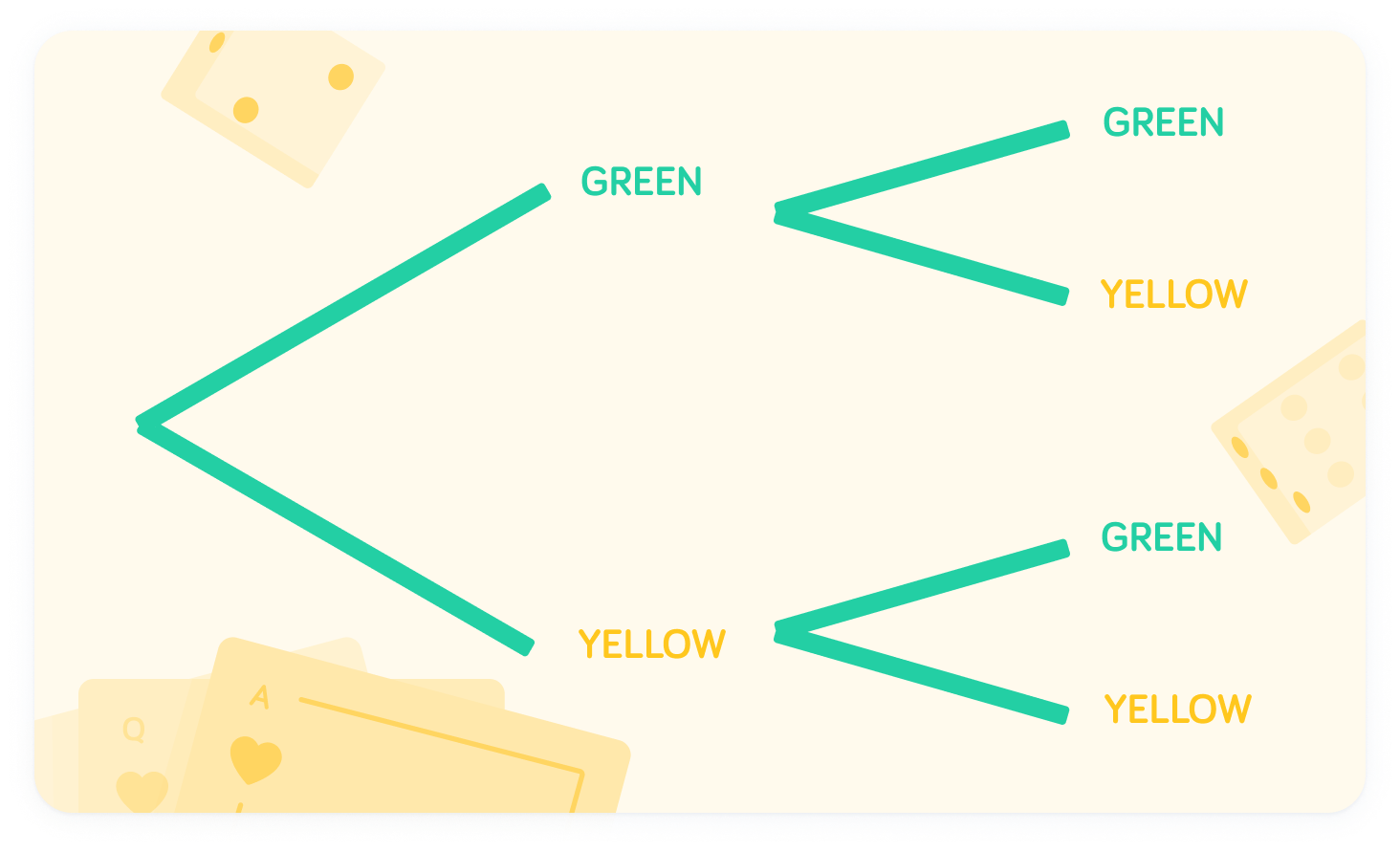
Let's find the probability of picking two balls of the same colour

The total number of green and yellow balls adds up to $n$

The probability of green is $\dfrac{3}{n}$

Since there are 3 green balls, we can write that P(Green) = $\dfrac{3}{n}$ .

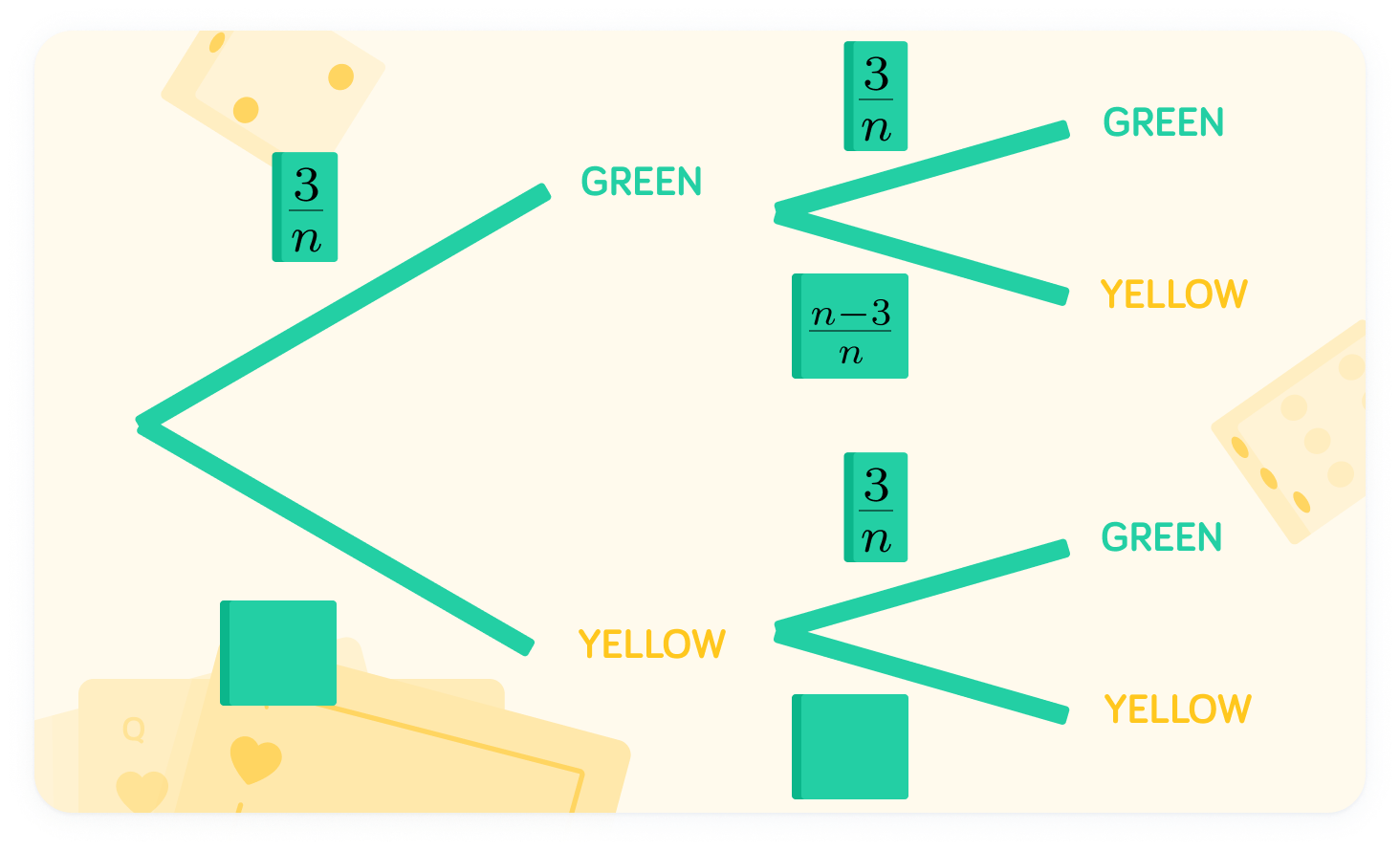
If green is $\dfrac{3}{n}$ , yellow is $\dfrac{n-3}{n}$

The total of green and yellow must add up to $n$ .

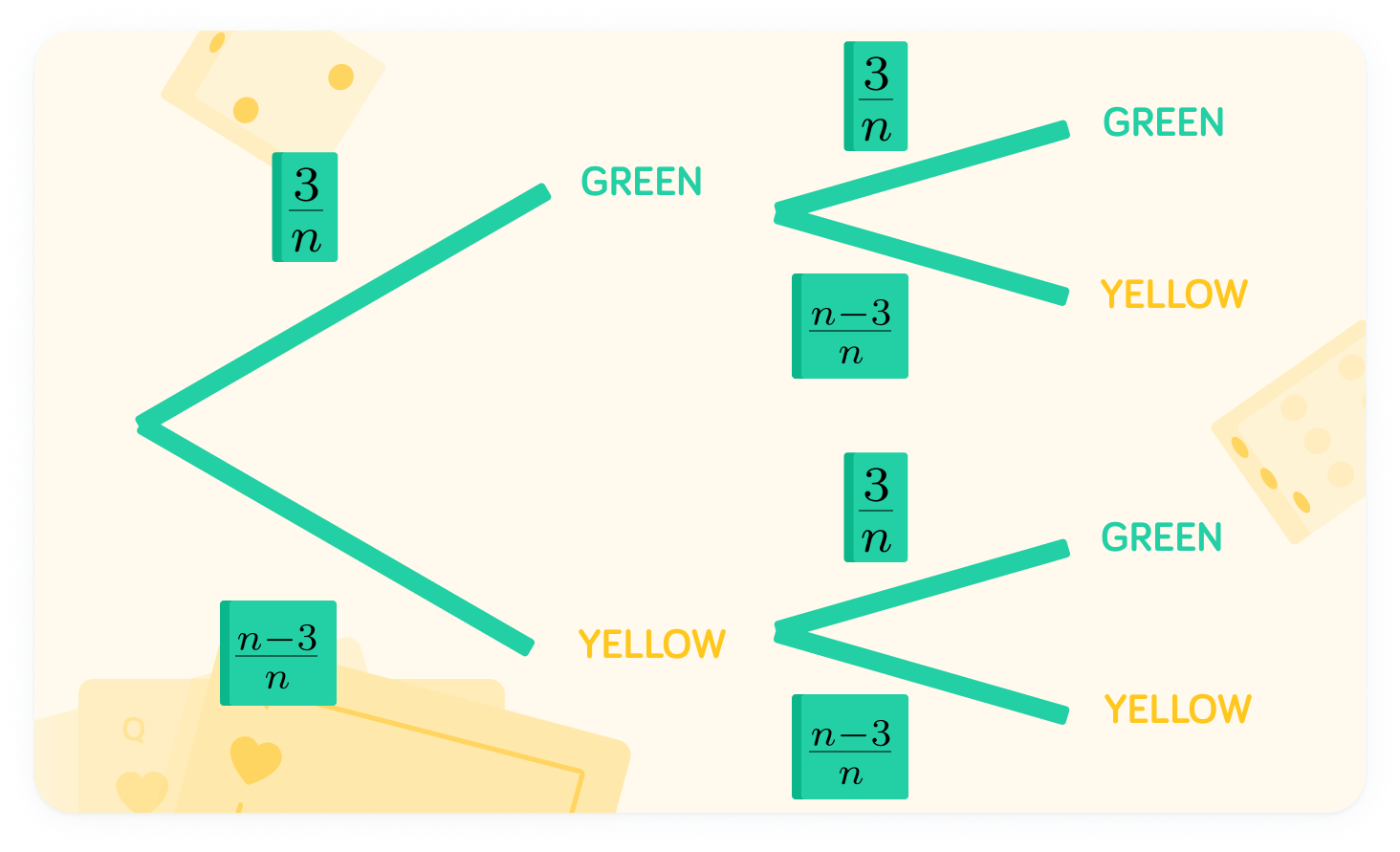
There are two routes to picking two balls of the same colour

The probability of two yellows is $\dfrac{(n-3)}{n} \times \dfrac{(n-3)}{n} = \dfrac{n^2 - 6n + 9}{n^2}$

What is the probability of picking two green balls?

The probability of two greens is $\dfrac{9}{n^2}$

To find this, we multiply the probabilities: $\dfrac{3}{n} \times \dfrac{3}{n}=\dfrac{9}{n^2}$

To find the probability of picking two of the same colour, add the probabilities

Since there are two routes to picking the same colour twice, we need to use the or rule of probability. Therefore, $P(same) = \dfrac{9}{n^2} + \dfrac{n^2 - 6n + 9}{n^2}$

What is $\dfrac{9}{n^2} + \dfrac{n^2 - 6n + 9}{n^2}$ ?

Nice!

The probability of the same colour twice is $\dfrac{\left(n^2-6n+18\right)}{n^2}$

In a box are $n$ sweets and chocolates, with 7 being sweets. How do we notate the amount of chocolates in the box?

Two balls are picked at random from a bag

There are 6 balls in total, with $n$ blue balls. The rest are red. The ball is replaced after the first pick. Given that the probability of picking two blue balls is $\dfrac{1}{6}$ , show that $n^2 - 6 = 0$

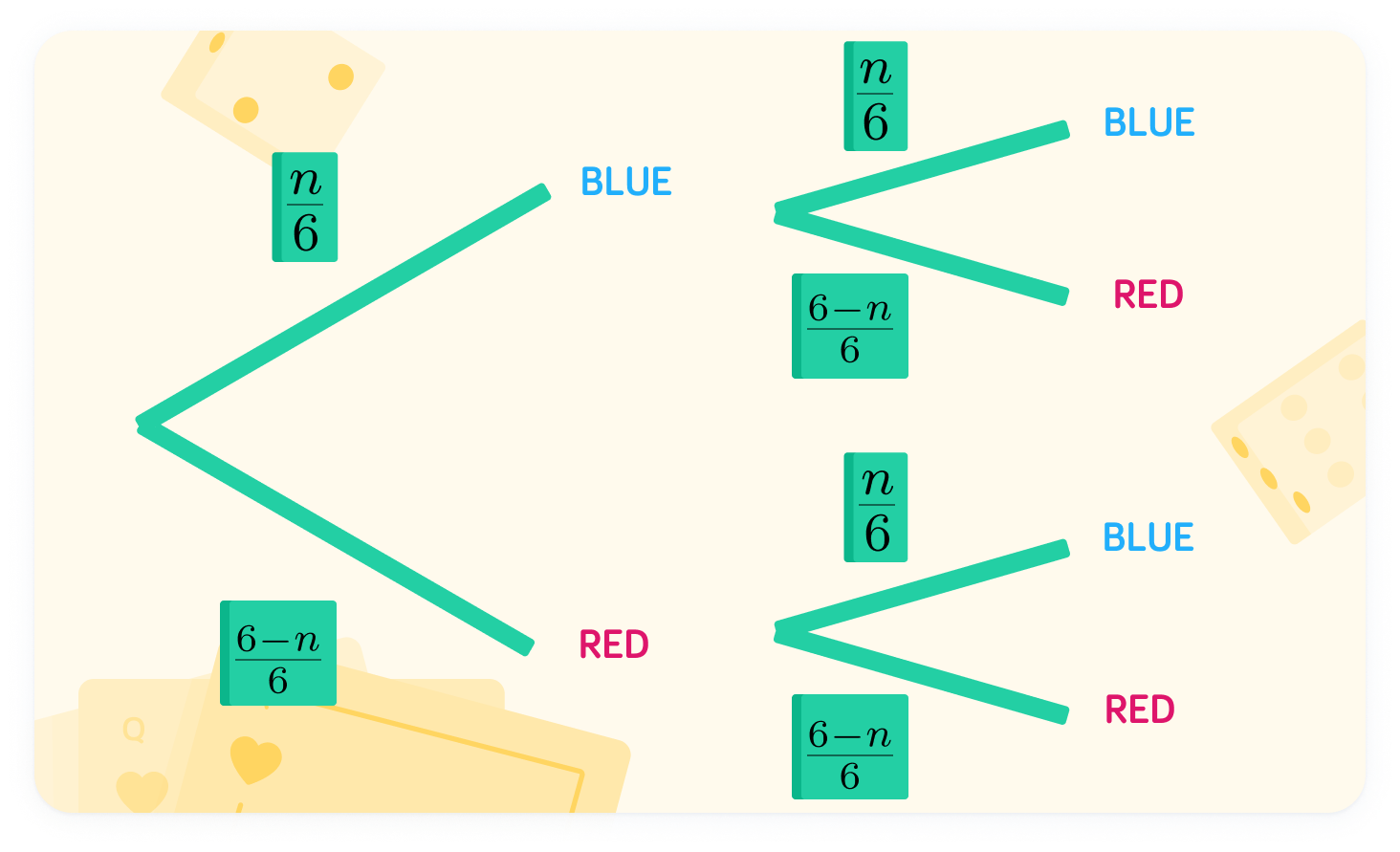
There are $n$ blue balls

Since there are 6 balls in total, the probability of blue is $\dfrac{n}{6}$

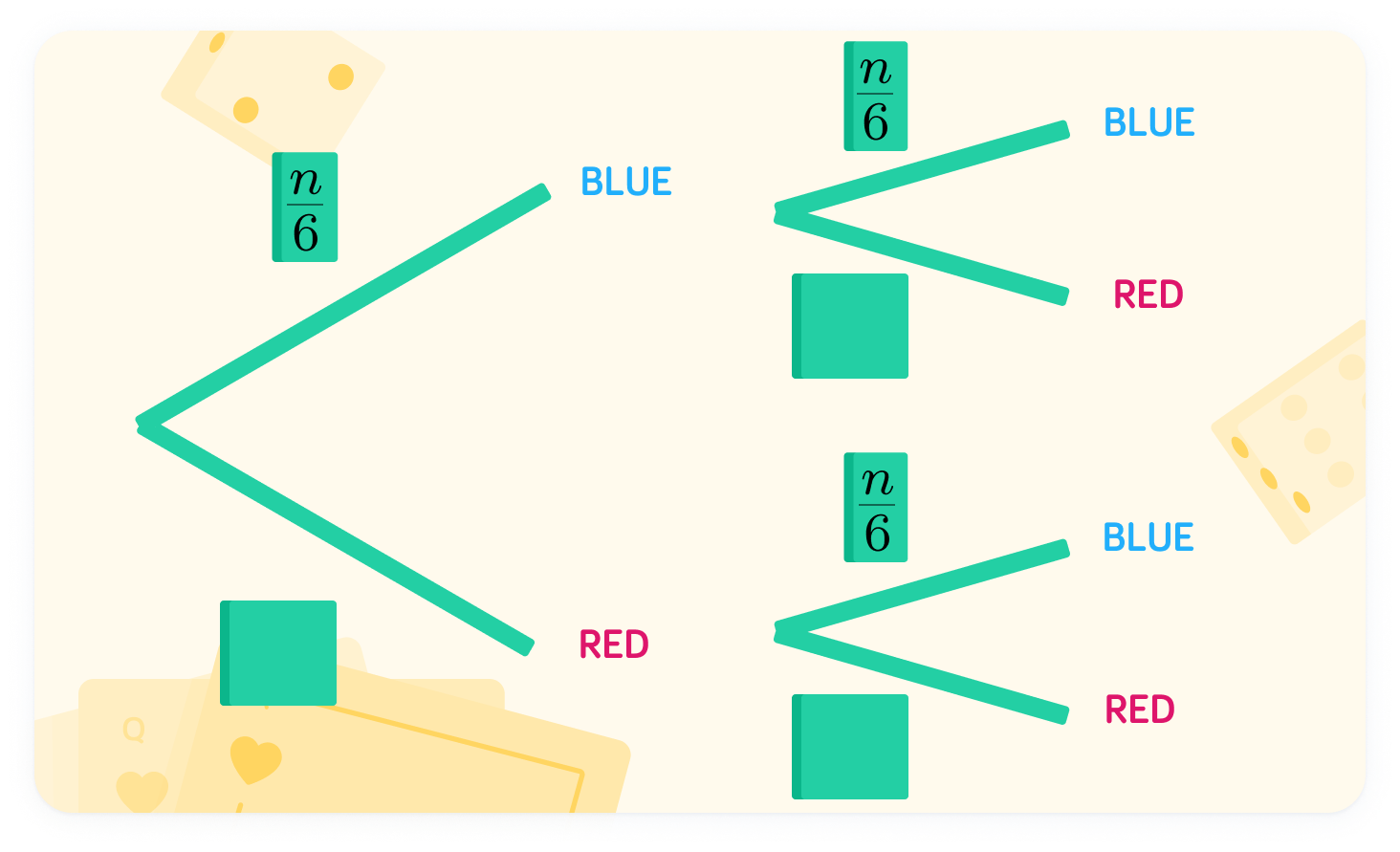
What is the probability of choosing a red ball?

The probability of red is $\dfrac{6-n}{6}$

Since there are 6 balls in total, we subtract the number of blue balls, $n$ , from the total.

What is the probability of two blue balls, as an expression containing $n$ ?

The probability of two blue balls is $\dfrac{n^2}{36}$

To find this, we multiply the probabilities of each individual blue ball: $\dfrac{n}{6} \times \dfrac{n}{36}=\dfrac{n^2}{36}$

The real probability of two blue balls is $\dfrac{1}{6}$ , as given in the question

Therefore, we can equate these two expressions: $\dfrac{n^2}{36}=\dfrac{1}{6}$ .

Rearrange $\dfrac{n^2}{36}=\dfrac{1}{6}$ to make $n^2$ the subject

By rearranging, we find $n^2=6$

To show that $n^2-6=0$ , we can subtract 6 from both sides.

Let's try another question with this example

This time, the probability of picking two reds in a row, when the first ball is replaced, is $\dfrac{2}{3}$

What is the probability of picking two red balls, as an expression involving $n$ ?

The probability of two reds is $\dfrac{n^2-12n+36}{36}$

$\dfrac{(n-6)(n-6)}{36}=\frac{n^2-12n+36}{36}$

Equate this to the real probability of two red balls, $\dfrac{2}{3}$

$\dfrac{n^2-12n+36}{36}=\dfrac{2}{3}$ . We want to show that $n^2 - 12n + 12 = 0$

Multiply both sides by 36

$\dfrac{n^2-12n+36}{36}=\dfrac{2 \times 36}{3} \space \rightarrow \space n^2-12n+36=24$

Subtract 24 from both sides

$n^2-12n+12=0$

Nice!

This is called a proof.