YOU ARE LEARNING:
Strategic Listing and the Product Rule for Counting
Strategic Listing and the Product Rule for Counting
In groups, there are many possible combinations of things. We can strategically list all options to make sure we cover every possible combination.
When you go to a café, you have many choices of food and drink. But how many possible combinations are there? And how can you ensure that you've explored every possible combination?
Strategic listing is a method of writing down all the possible combinations in a list of items.
Let's have a look at an example
You win tickets to a musical and have a choice of a few friends to take along with you. But, you can only take two of them, one boy and one girl. What are all the possibilities?
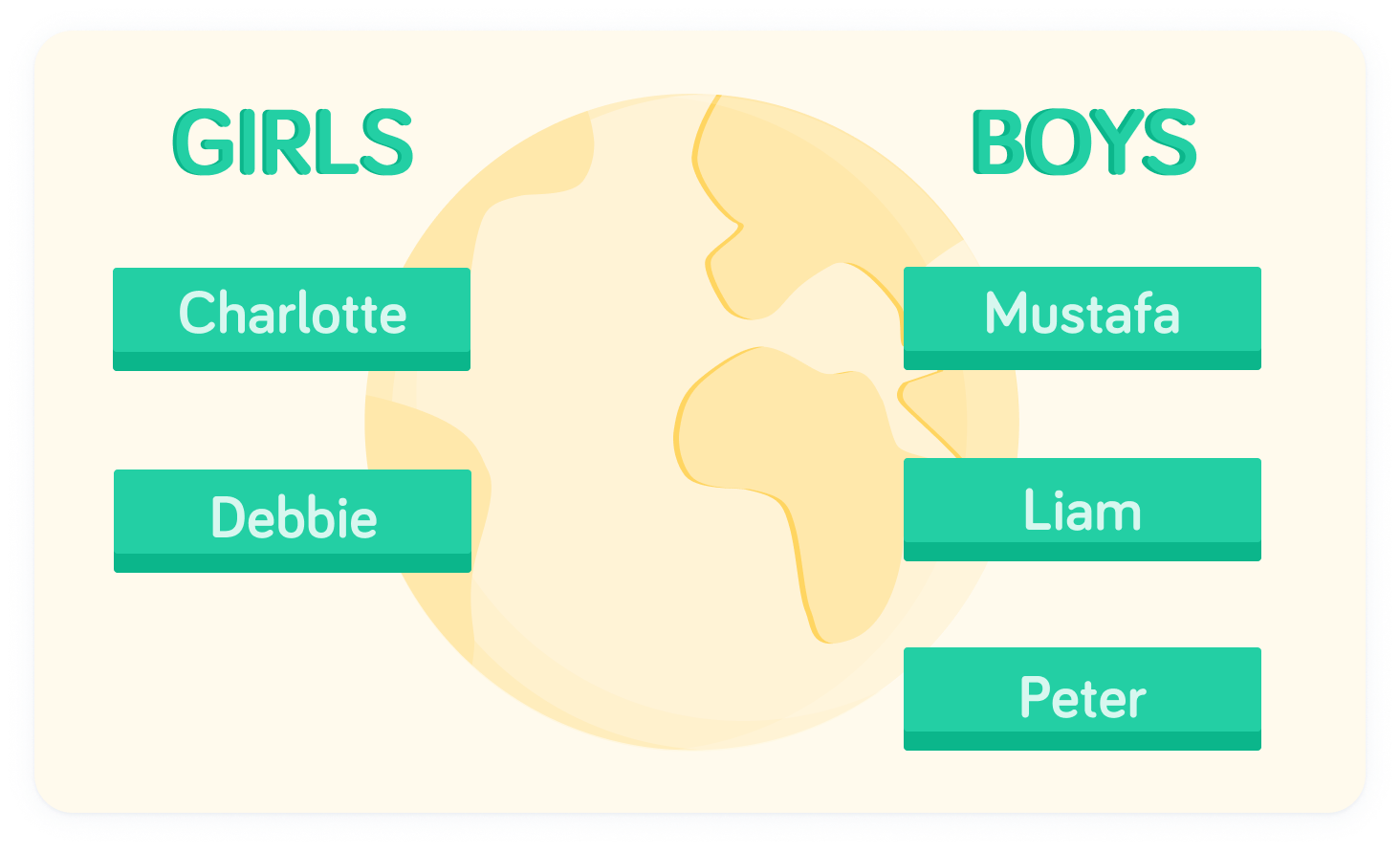
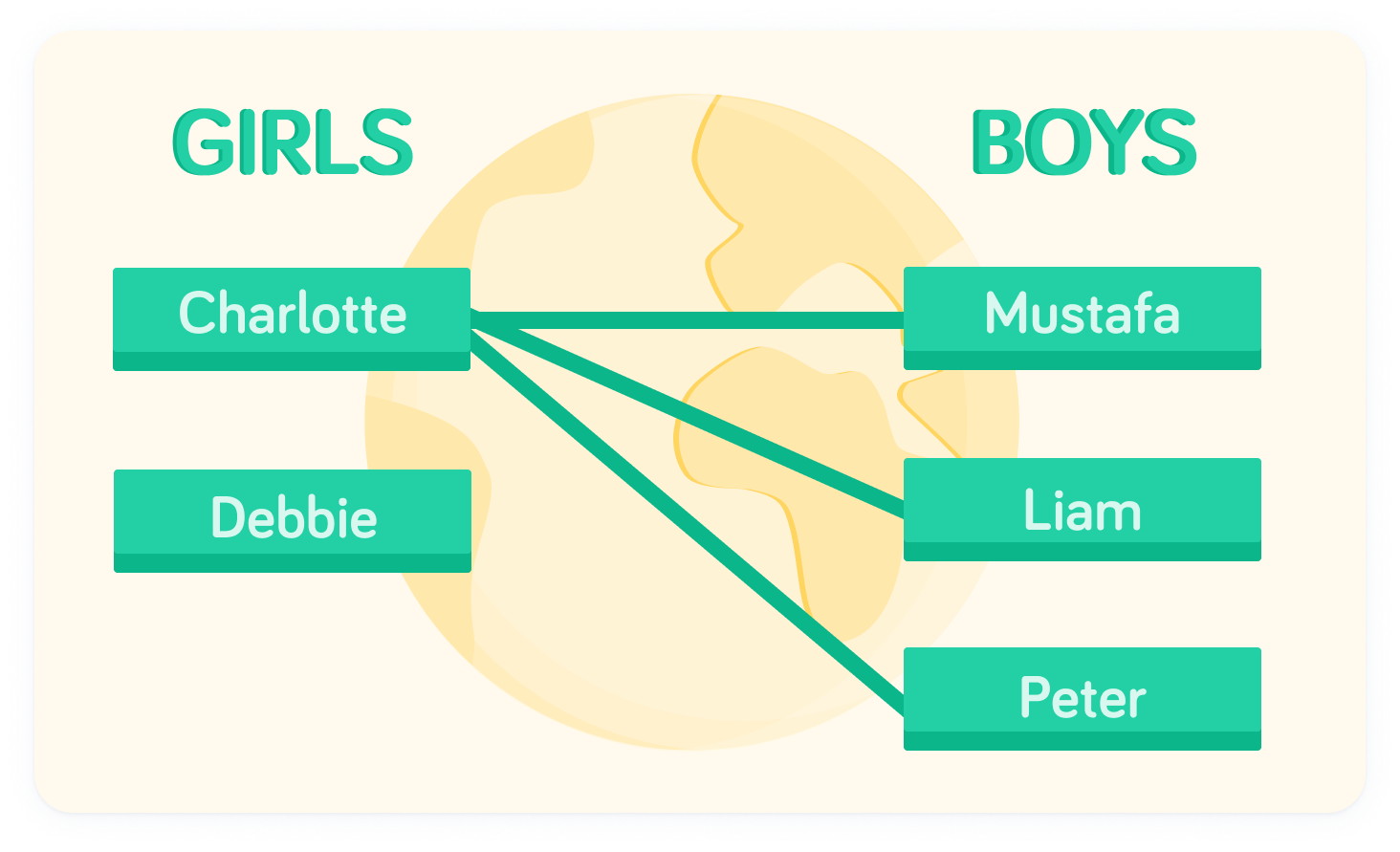
Take Charlotte as the girl
There are three options if Charlotte is picked as the girl: Charlotte and Mustafa, Charlotte and Liam, or Charlotte and Peter. We can list each of these down.
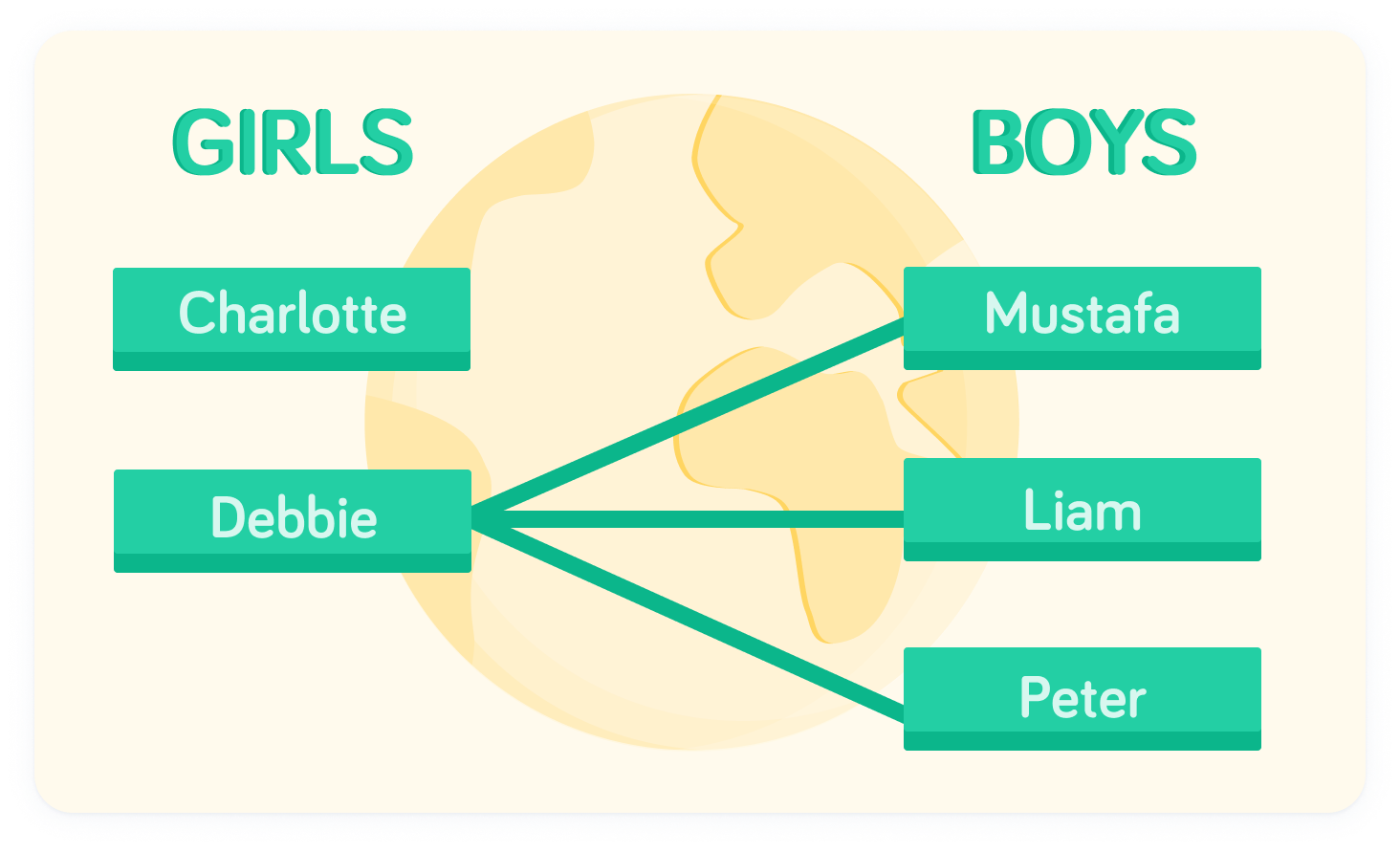
What about if Debbie is chosen as the girl?
There are also three options: Debbie and Mustafa, Debbie and Liam, or Debbie and Peter. We can also list each of these down
We have listed out all the possible combinations
Notice that by starting with each girl, and listing the possible pairings, we can ensure that we haven't missed any combinations.

How many possible combinations are there of one boy and one girl?


What is the probability of picking Debbie and Liam as a combination?


There is a faster way to find the number of combinations without listing all options. This is called the product rule for counting.
The product rule for counting, where there are two or more events, involves multiplying the number of outcomes of each event together.
Let's look at our example again
You win tickets to a musical and have a choice of a few friends to take along with you. But, you can only take two of them, one boy and one girl. What are all the possibilities?

There are two girls and 3 boys to choose from
In other words, there are 2 outcomes for choosing a girl, and 3 outcomes for choosing a boy. To use the product rule for counting, we can multiply these numbers together.

How many possible combinations are there?


