Probability & Statistics

YOU ARE LEARNING:

Probability Tree Diagrams and Conditional Events

Probability Tree Diagrams and Conditional Events

In many situations, one event happening influences the chance of another event happening. We can also use tree diagrams to map out situations like these, and find probabilities of multiple events.

When multiple events happen, it is possible that one event happening can influence the chance of another happening. These types of events are called conditional events.

When its raining, you are more likely to avoid walking to the shop; when you have lots of work, you are less likely to go out with your friends. Conditional events are all around us in life.

We can also use tree diagrams to represent conditional probabilities. The difference here is that the probabilities change between branches of different events.

Let's look at an example

Jordan works on Monday and Tuesday mornings. The probability of being on-time on Monday is $0.7$ . If Jordan is on-time on Monday, the probability he will be on-time on Tuesday decreases to $0.5$ . If Jordan is late on Monday, the probability he will be late on Tuesday is $0.9$ .

Let's find the chance he will be late on exactly one day

There are multiple ways this can happen. Therefore, we need to add together the probabilities of each of the individual paths.

What is the probability of him being late on Monday?

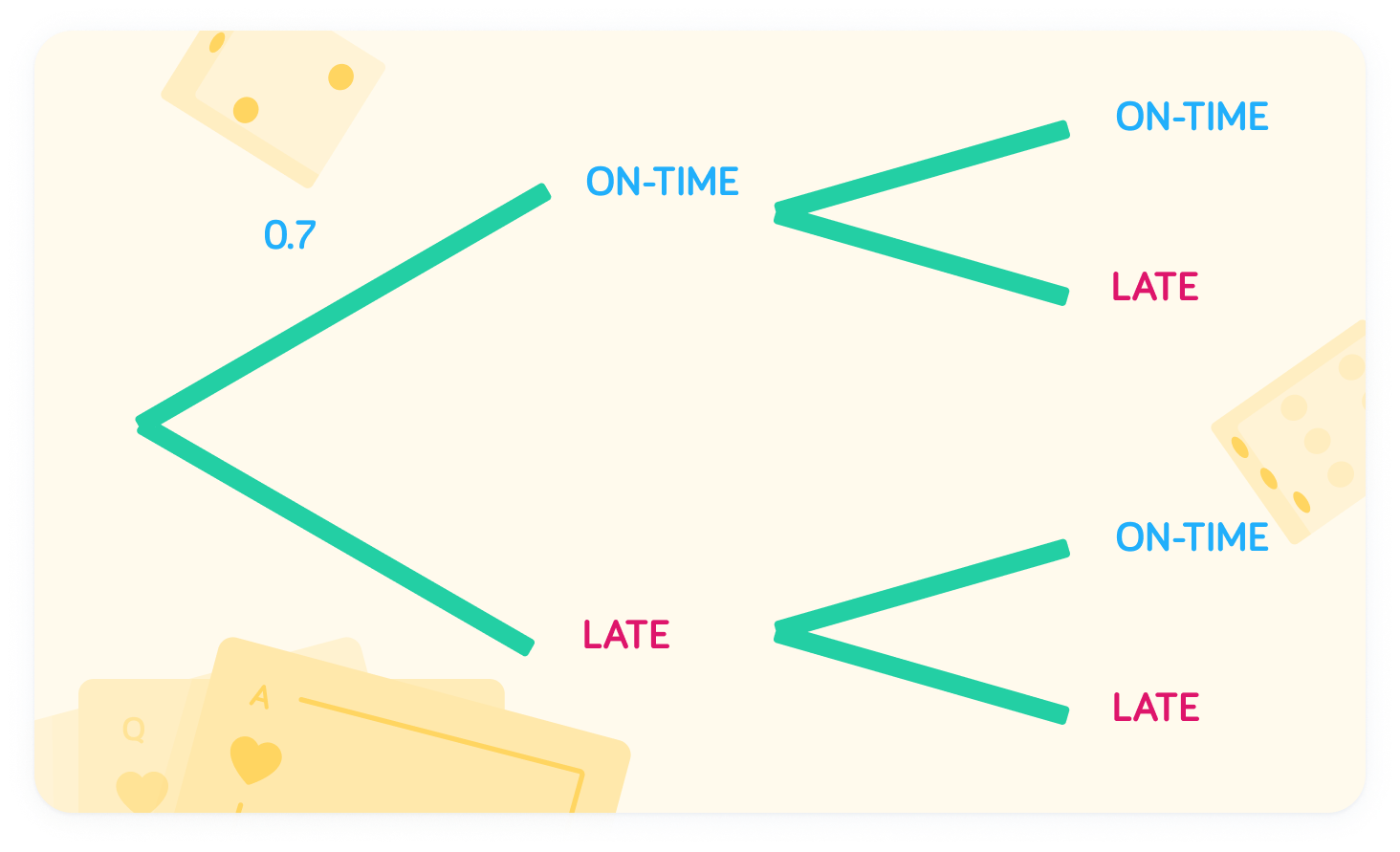
The probability of being late on Monday is $0.3$

Since these are the only two outcomes on Monday, the probability is $1-0.7=0.3$

Now we can add the probabilities for Tuesday

If Jordan is on-time on Monday, the probability of him being on-time on Tuesday will change to $0.5$ . So we are looking at the top two branches for Tuesday - once Jordan has been on-time to work on Monday.

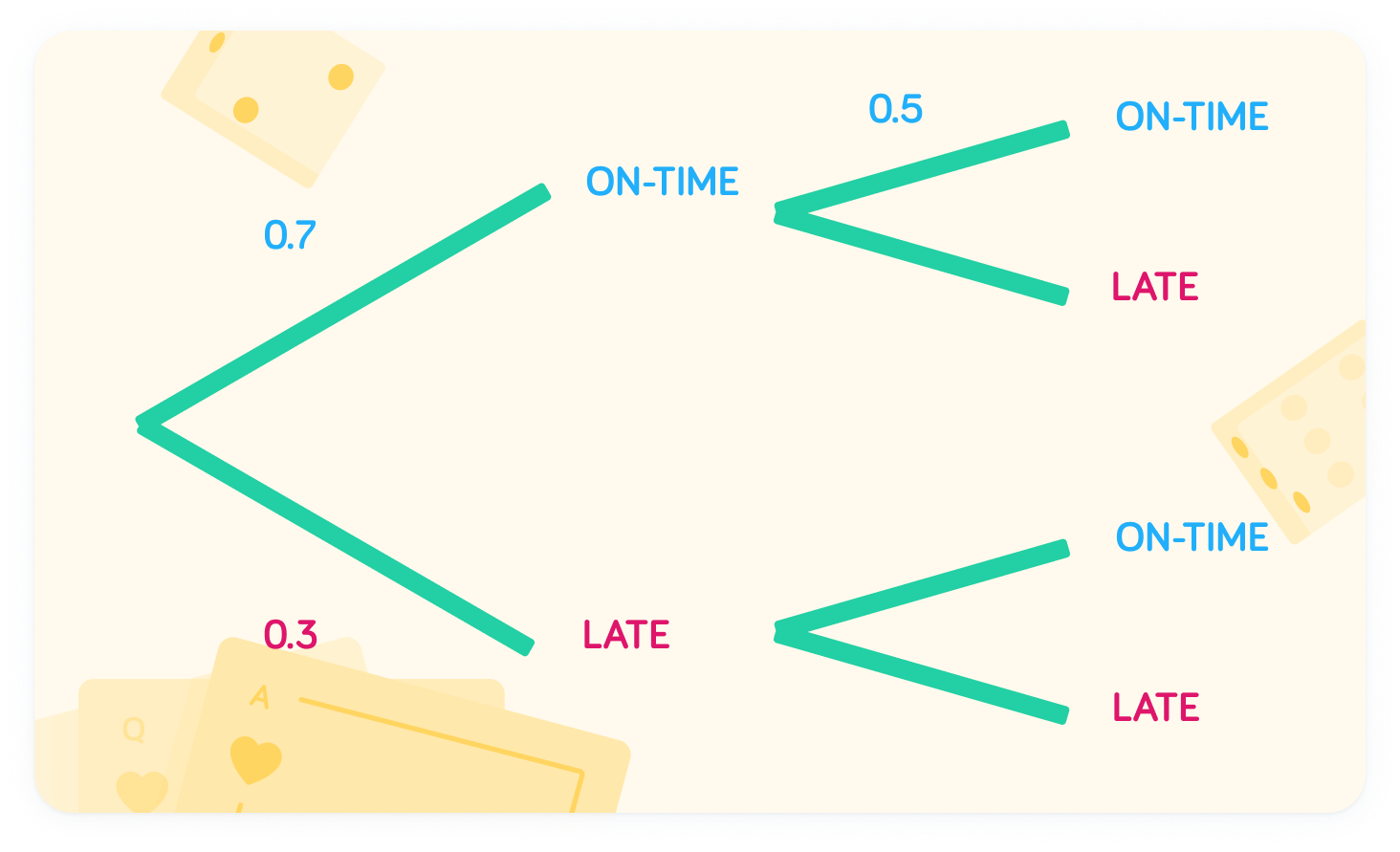
What is the probability of Jordan being late on Tuesday if on-time on Monday?

The probability is $0.5$

Since these are the two outcomes on Tuesday, after being on time on Monday, the probability is $1-0.5=0.5$

This is the full tree diagram

The tree plots out the different probabilities depending on Jordan's timeliness on Monday.

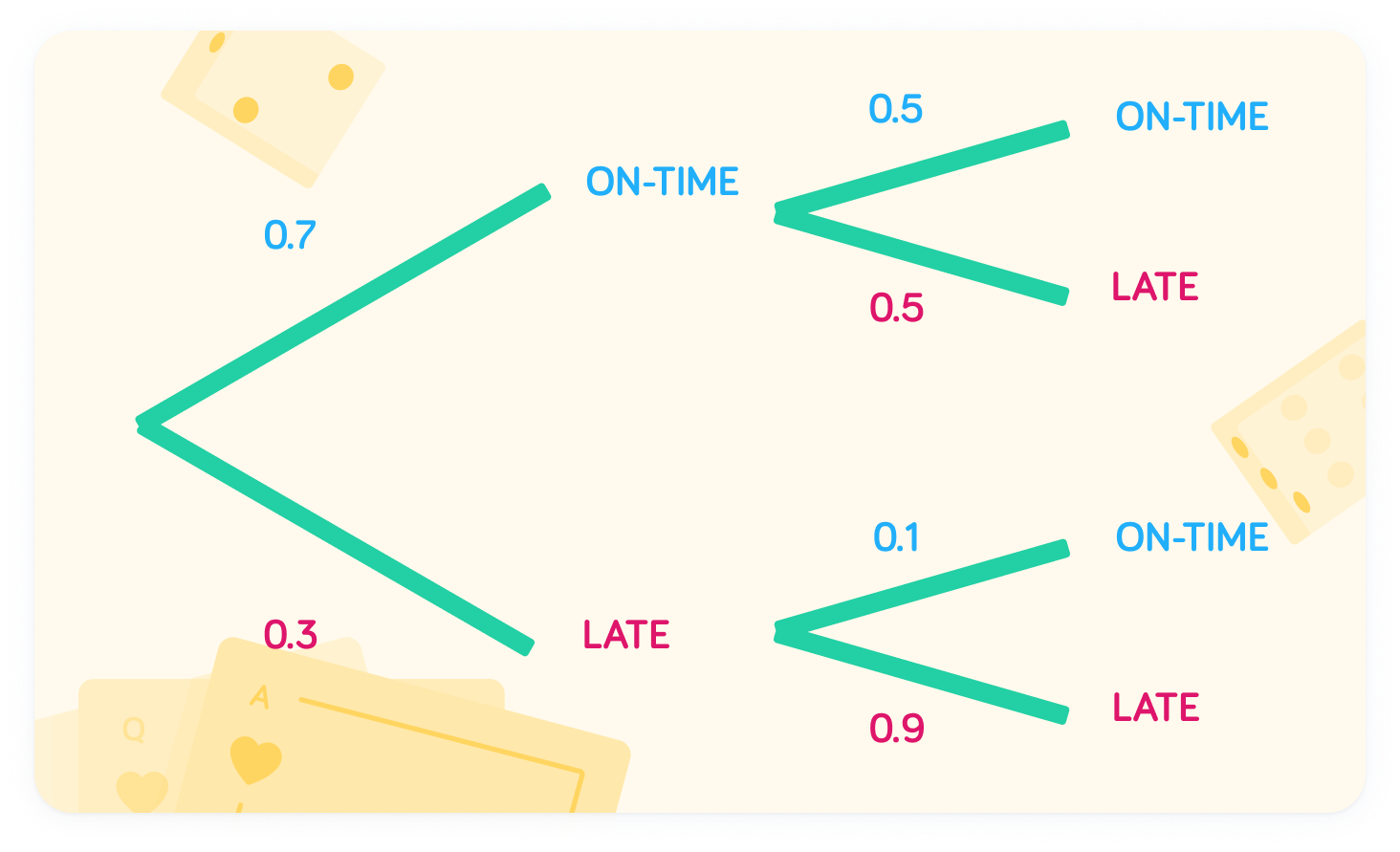
Now we can find the chance of being late on one day

There are two ways to do this. Late/on-time, or on-time/late. We should add these probabilities together to find the probability of either happening.

What is the probability of being on-time on Monday, then late on Tuesday?

The probability of this is $0.35$

To find this, we multiply the probabilities together. $0.7 \times 0.5 = 0.35$ .

What is the probability of being late on Monday, then on-time on Tuesday?

The probability is $0.03$

We can find this by multiplying the probabilities together: $0.3 \times 0.1=0.03$

To find the probability of either, add them together

We want to find the probability of being late on just one day, so we should add together: $0.03+0.35$

What is $0.03+0.35$ ?

Nice!

The chance of being late on one day is $0.38$

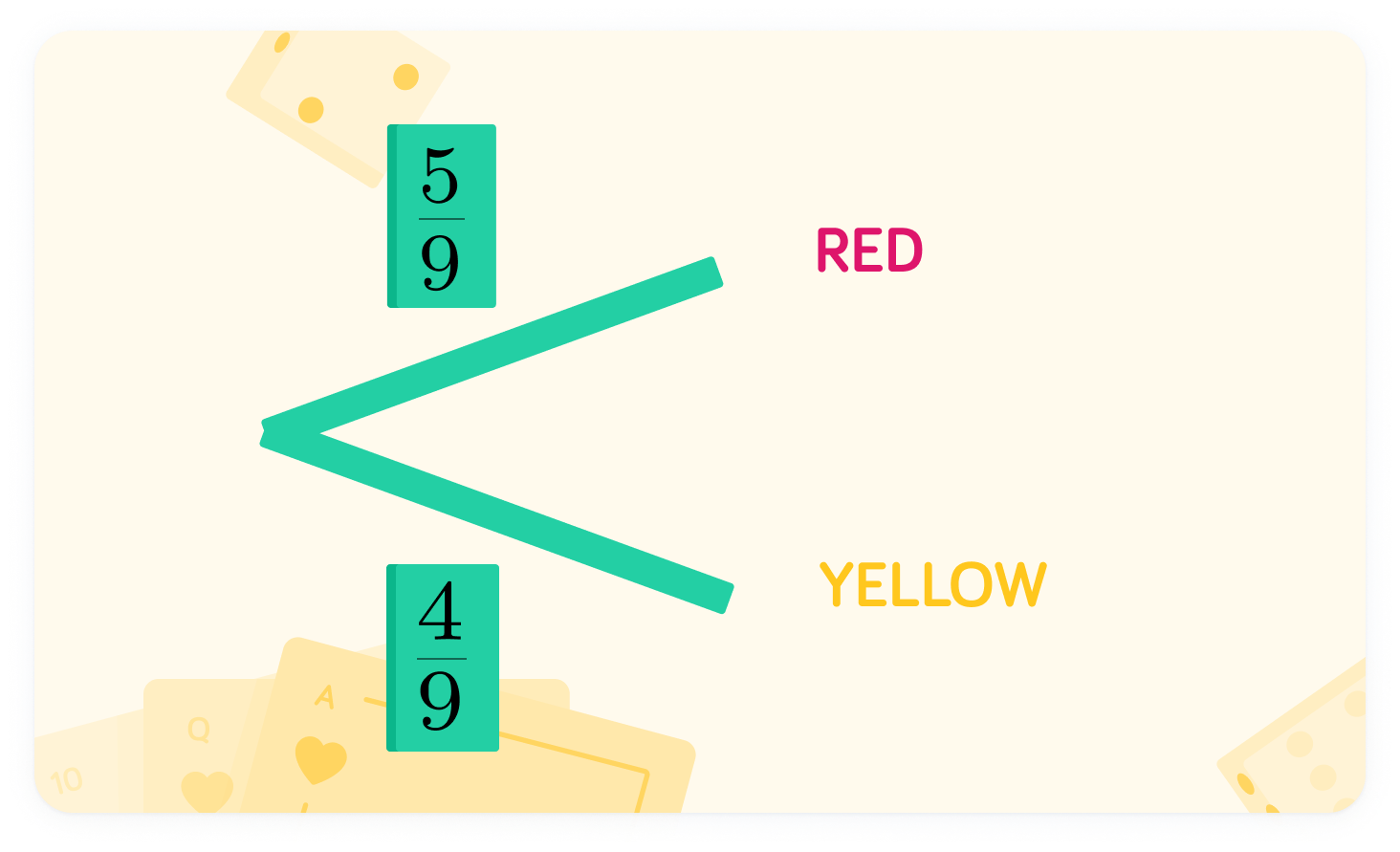
In a bag there are 5 red and 4 yellow balls

Ali pick two balls at random. However, after the first ball, Ali does not replace the ball. Let's find the probability of Ali picking two balls of the same colour.

For the first ball, what is the probability of picking a red ball?

The probability of a red is $\frac{5}{9}$

There are 9 total balls, and 5 of them are red.

What is the probability of the first ball being yellow?

The probability of the first ball being yellow is $\dfrac{4}{9}$

There are 9 total balls, and 4 of them are yellow.

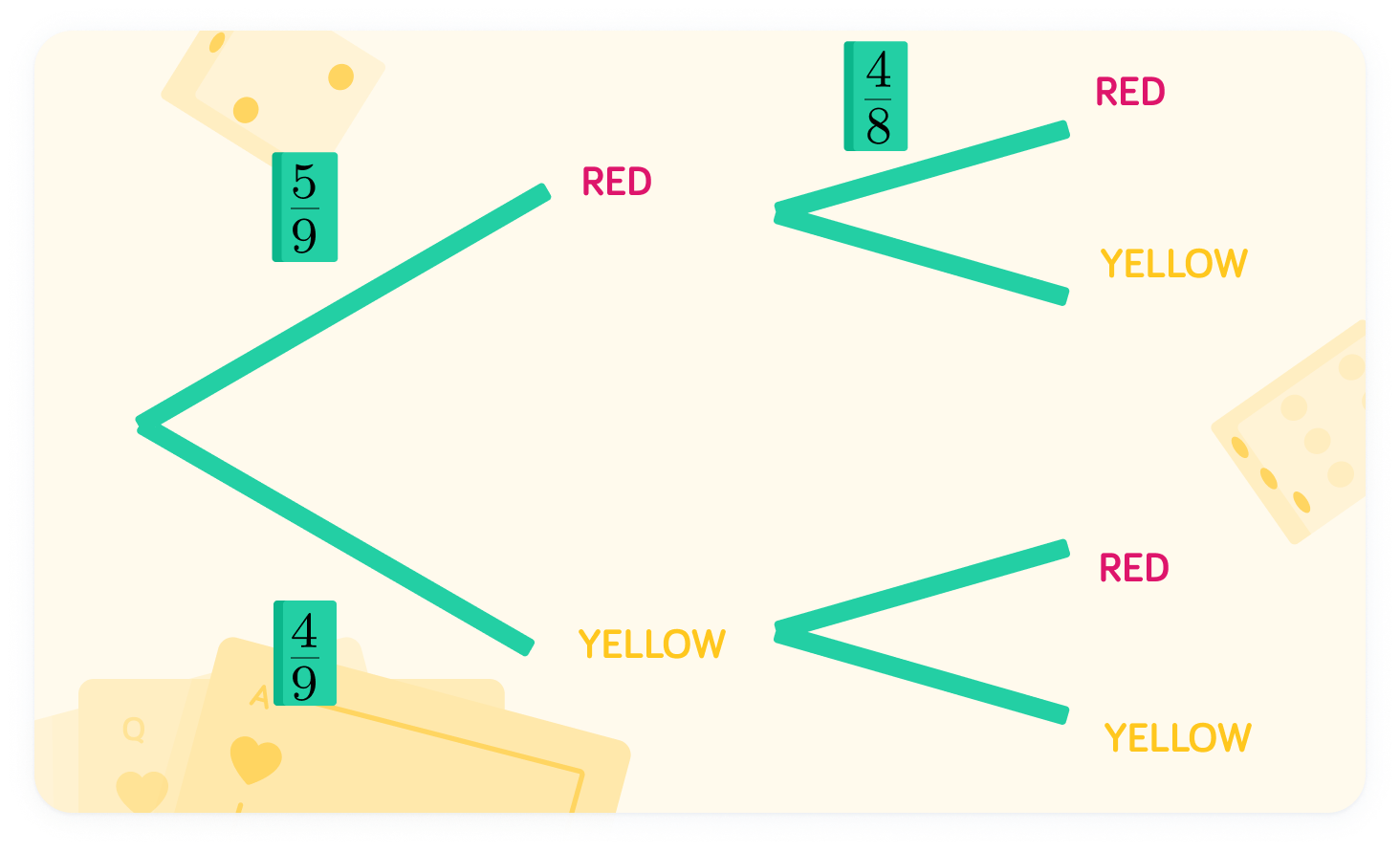
We can plot this in a tree diagram

This describes the probabilities of the first ball that is picked.

Ali picks a red ball first

Since he doesn't replace it, there will be fewer balls to choose from on his second pick. Therefore, the probabilities in the second round.

How many balls are there now to choose from?

There are 8 balls to choose from now

Therefore, each of the probabilities in the second pick will contain 8 as the denominator.

The first ball is red

Therefore, there is one less ball overall, but also one less red ball. Therefore, the probability of picking a red ball on the second round is $\dfrac{4}{8}$

What is the probability of picking a yellow on the second round?

The probability is $\dfrac{4}{8}$

Since the first ball was red, there is still the same amount of yellow balls. However, notice that the proportion of yellow balls has increased, and the probability of red and yellow is now equal.

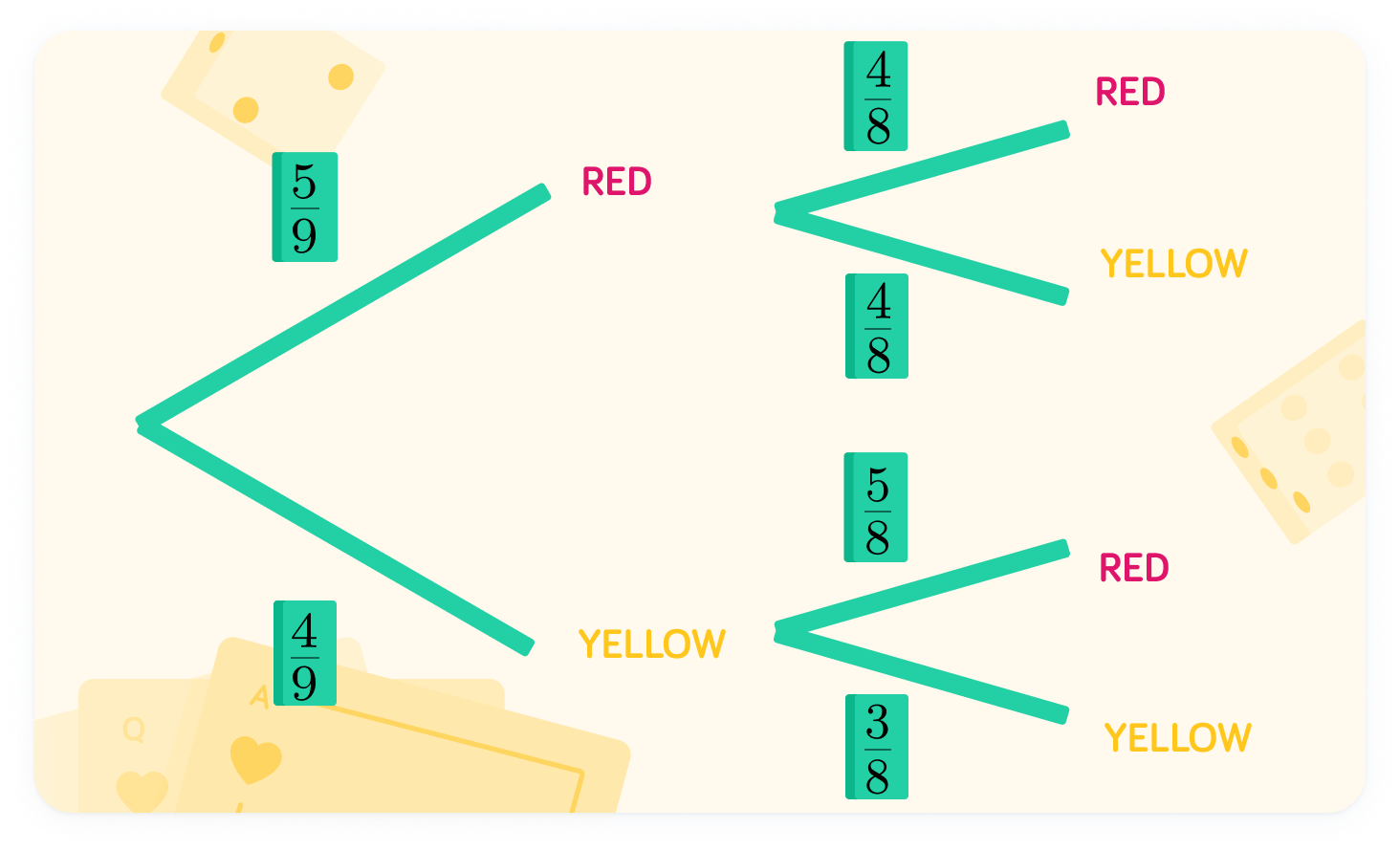
Let's look at what happens if the first ball is yellow

This time, there is still one ball missing in the second round. However, the ball missing is yellow, so the probabilities are slightly different.

What is the probability of the second ball being yellow, if the first is also yellow?

The probability of the second being yellow is $\dfrac{3}{8}$

Notice that since the first ball is yellow, there are still the same amount of red balls. However, the proportion has changed for both balls.

So what is the probability of picking two the same colour?

There are two routes to picking the same colour. Therefore, we need to add together the probability of each one.

What is the probability of two yellow?

What is the probability of two reds?

Let's add these together

The probability of two yellows is $\dfrac{12}{72}$ , and the probability of two reds is $\dfrac{20}{72}$

What is $\dfrac{12}{72}+\dfrac{20}{72}$ ?

The probability of two colours the same is $\dfrac{32}{72}$

We can simplify this to $\frac{5}{9}$ . This is our final answer!