YOU ARE LEARNING:
Probability Tree Diagrams and Independent Events 1

Probability Tree Diagrams and Independent Events 1
Probability tree diagrams allow us to map out the probability of multiple events happening in sequence.
Probability tree diagrams are a great way to display all the possibilities when we need to work out the combined probability of more than one event happening.
What is the correct calculation for finding the combined probability of two events happening?

There are 6 red balls and 7 yellow balls in a bag
Grace removes one ball from the bag, writes down the colour and replaces the ball back into the bag. Grace then removes another ball from the bag.
We can plot this on a tree diagram
In the first round, Grace can choose either a red ball or a yellow ball. Therefore, we can display these outcomes as 'branches'.

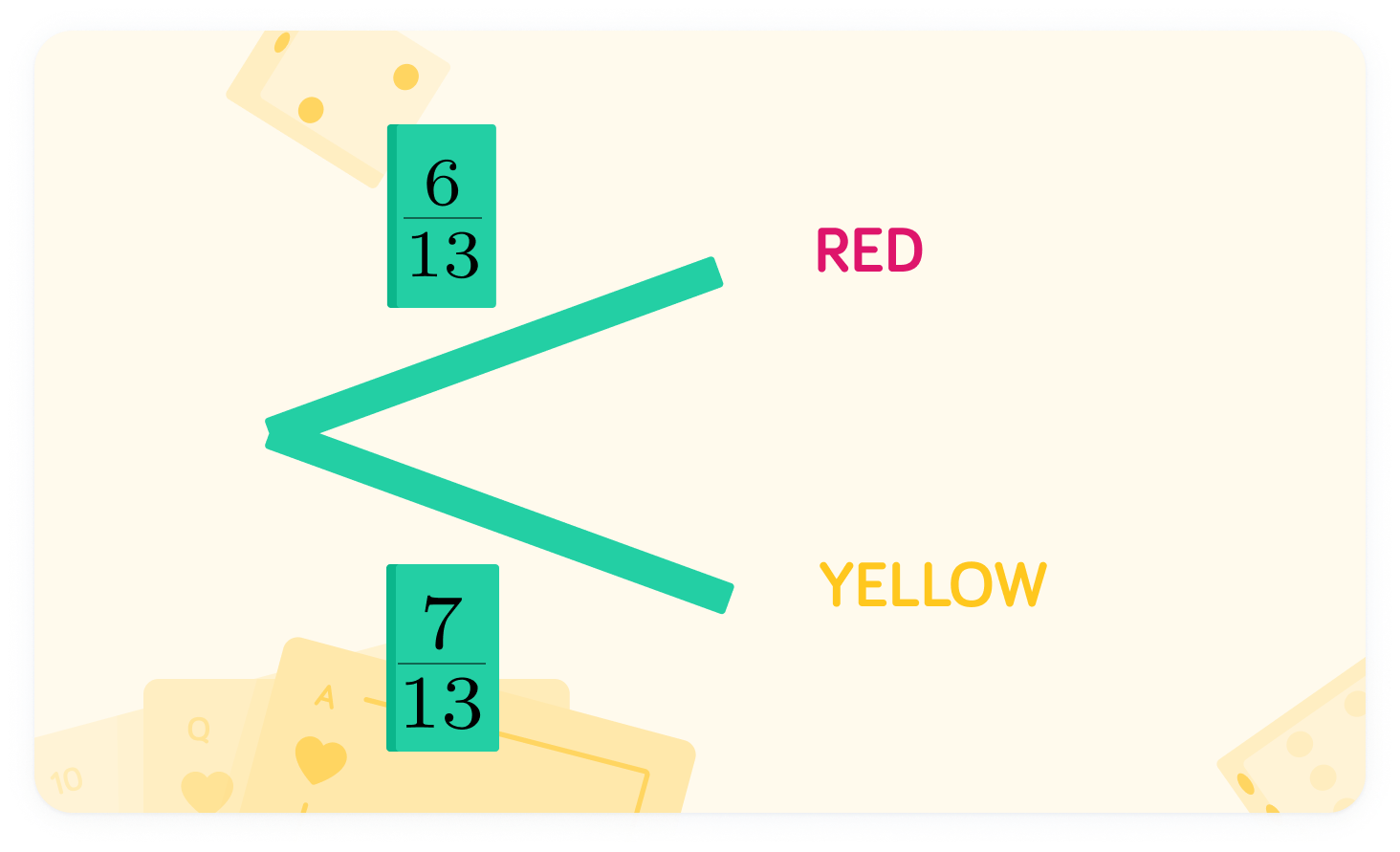
We can assign these outcomes probabilities
There are 6 red and 7 yellow balls in the bag. 6+7=13, so there are 13 balls in total. We can see that 7 out of 13 balls are yellow, so we can assign it the probability 137.

The probability of yellow is 137. What is the probability of red?


The probability of red is 136
We can display these probabilities on the corresponding branches.
But wait!
Grace replaces the ball, and takes another ball out of the bag.

What is the probability of picking a yellow ball, if the first ball is replaced?


The probability is the same the second time
Now our probability tree is complete, we can work out the combined probability of different ball combinations.

Let's find the probability of Grace picking two balls of the same colour
There are two ways this can happen. Either Grace can pick two red balls in a row, or two yellow balls in a row.

The probability of two reds is 16936
We can find this by applying the "and" rule. 136×136=16936

What is the probability of picking two yellow balls?


The probability of two yellows is 16949
Each time, yellow has the probability 137. So the probability of both being yellow is 137×137=16949

We can add these together to find the combined probability
As there are two ways to pick the same colour twice in a row, we need to add the probabilities together.

What is 16949+16936?


The combined probability is 16985
We can write this as P(same colours)=16985

Let's find the probability of picking different colours
This could happen if Grace picks a red ball first and then a yellow ball OR if Grace picks a yellow ball first and then a red ball. Note that the order is very important, as they are two different scenarios!

What is the probability of yellow then red?


The probability of yellow then red is 16942
We can find this by multiplying the probabilities together. 137×136=16942

What is the probability of red then yellow?


The probability of red the yellow is also 16942
We can find this by multiplying the probabilities together. 136×137=16942

Add these together to find the probability of picking different colours
As there are two ways to pick different coloured balls across the two events, we can add the probabilities together.

What is the probability of picking two different colours, if both scenarios are 16942?


The combined probability is 16984
We can write this probability as P(Different Colours)=16984

Now let's find the probability of picking at least one yellow ball
There are three possibilities to include here. Our calculation could therefore be P(Yellow,Yellow)+P(Yellow,Red)+P(Red,Yellow)

However, there is only one possibility that's not included
The only way to not pick a yellow ball at least one of the times is to pick red both times. Therefore, we can find the probability of picking red both times, and subtract this from the total probability.

What is the probability of picking red both times?


P(Red,Red)=16936
We can take this value away from the total probability, 1, to find the probability of picking at least one yellow.

What is 1−16936?


The probability of at least one yellow is 169133
Nice!

